Irisデータセットの探索的データ分析
【概要】このページでは、Irisデータセットを用いた探索的データ分析の基礎を学ぶ。データ構造の理解、基本統計量の算出、複数の可視化手法による特徴把握を通じて、データ分析の基本的な手順と考え方を習得できる。Google Colabで実行可能なプログラムを提供し、実験計画から結果の考察までの一連の流れを解説する。
Colabのページ(ソースコードと説明): https://colab.research.google.com/drive/1Dqsy_3jsz_yoCW35t9cN-h7f6Eu_PwFM?usp=sharing
【目次】
用語リスト
データ構造
DataFrame
pandasライブラリが提供する表形式のデータ構造である。行と列で構成され、各列に名前(列名)がある。このコードでは、Irisデータセットを格納するために使用されている。
配列(numpy.ndarray)
NumPyライブラリが提供する数値データの集まりである。このコードでは、scikit-learnから読み込んだデータを格納している。
列(カラム)
DataFrameの縦方向のデータである。このコードでは、がく片の長さ、がく片の幅、花弁の長さ、花弁の幅、種名の5つの列がある。
行(サンプル)
DataFrameの横方向のデータである。このコードでは、1つの行が1つの花のデータを表す。150行ある。
基本統計量
平均(mean)
データの合計をデータ数で割った値である。データの中心的な傾向を示す。
標準偏差(std)
データのばらつきの大きさを示す値である。標準偏差が大きいほどデータが平均から離れている。
最小値(min)、最大値(max)
データの中で最も小さい値と最も大きい値である。データの範囲を把握できる。
四分位数
データを小さい順に並べたとき、25%の位置(第1四分位数)、50%の位置(中央値)、75%の位置(第3四分位数)の値である。このコードでは25%、50%、75%として表示される。
相関係数
2つの特徴量の関係の強さを-1から1の値で示す。1に近いほど正の相関(一方が増えると他方も増える)、-1に近いほど負の相関(一方が増えると他方は減る)、0に近いほど関係がないことを示す。
可視化
ヒストグラム
データの分布を棒グラフで表示する。横軸が値の範囲、縦軸が頻度(その範囲に含まれるデータの数)である。
散布図
2つの特徴量の関係を点で表示する。横軸と縦軸にそれぞれ異なる特徴量を配置し、各データを点として描く。
箱ひげ図(box plot)
データの分布を箱と線で表示する。箱の中央の線が中央値、箱の上下が第1・第3四分位数、箱から伸びる線(ひげ)が最小値・最大値付近、点が外れ値を示す。
ヒートマップ
数値データを色の濃淡で表現する図である。このコードでは、相関係数を色で表示している。
ペアプロット
複数の特徴量の組み合わせを一度に表示する散布図の集まりである。このコードでは、最初の2つの特徴量の関係を種別に表示している。
データ処理
欠損値
データが記録されていない部分である。このコードでは、isnull()メソッドで欠損値の有無を確認している。
データ型(dtype)
各列に格納されているデータの種類である。数値(float、int)、文字列(object)などがある。
インデックス
DataFrameの各行を識別するための番号または名前である。このコードでは0から149までの番号が割り振られている。
プログラム利用ガイド
1. このプログラムの利用シーン
データ分析の基礎を学習する際に、Irisデータセットの構造と特性を理解するためのツールである。統計量の確認、可視化手法の実践、種別間の特徴比較を通じて、探索的データ分析の基本を習得できる。
2. 主な機能
- データセットの自動読み込み: scikit-learn組み込みのIrisデータセットを取得する
- 基本統計量の表示: 各特徴量の平均、標準偏差、最小値、最大値、四分位数を出力する
- 6種類のグラフ生成: ヒストグラム、散布図、箱ひげ図、相関ヒートマップ、ペアプロットを一括作成する
- 種別ごとの可視化: 3種のアヤメを色分けして、特徴量の分布と関係性を比較する
- 相関分析: 特徴量間の相関係数を算出し、ヒートマップで表示する
3. 基本的な使い方
- Colabのページを開く
Colabのページ(ソースコードと説明): https://colab.research.google.com/drive/1Dqsy_3jsz_yoCW35t9cN-h7f6Eu_PwFM?usp=sharing
- データセット情報、統計量、グラフが表示される
- 各グラフの説明がコンソールに出力される
4. 便利な機能
- 包括的な分析結果: 1つのプログラムで、データの読み込みから可視化まで完結する
プログラムの説明
概要
このプログラムは、Irisデータセットを用いた探索的データ分析を実行する。データの構造把握、統計量の算出、複数の可視化手法による特徴の把握を行う。
主要技術
探索的データ分析(Exploratory Data Analysis, EDA)
John Tukeyが1970年代に開発したデータ分析手法である[2]。データセットの主要な特性を要約し、統計グラフィックスと可視化を用いてパターン、異常値、変数間の関係性を発見する[3]。
Irisデータセット
Ronald Fisherが1936年に導入した分類問題の古典的データセットである[1]。3種のアヤメ(Setosa、Versicolor、Virginica)について、がく片と花弁の長さと幅の4特徴量を150サンプル収録する[4]。scikit-learnライブラリに組み込まれている。
技術的特徴
- 複数の可視化手法の統合
ヒストグラム、散布図、箱ひげ図、相関ヒートマップ、ペアプロットの6種類のグラフを生成し、多角的にデータを分析する。
- Pythonデータ分析ライブラリの統合
Pandas(データ操作)、NumPy(数値計算)、Matplotlib(基本可視化)、Seaborn(統計的可視化)を組み合わせる[5][6]。
- 統計的サマリーの自動生成
基本統計量(平均、標準偏差、四分位数)、欠損値の確認、相関係数の算出を自動実行する。
- 種別ごとの比較分析
3種のアヤメについて、特徴量の分布と関係性を色分けして可視化し、種間の差異を明確にする。
参考文献
[1] Fisher, R. A. (1936). The Use of Multiple Measurements in Taxonomic Problems. Annals of Eugenics, 7(2), 179-188.
[2] Tukey, J. W. (1977). Exploratory Data Analysis. Addison-Wesley.
[3] IBM. (2024). What is Exploratory Data Analysis? https://www.ibm.com/think/topics/exploratory-data-analysis
[4] scikit-learn developers. load_iris — scikit-learn documentation. https://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_iris.html
[5] Waskom, M. An introduction to seaborn. https://seaborn.pydata.org/tutorial/introduction.html
[6] pandas development team. pandas documentation. https://pandas.pydata.org/
実験・研究スキルの基礎:Google Colabで学ぶ探索的データ分析実験
1. 実験・研究のスキル構成要素
実験や研究を行うには、以下の5つの構成要素を理解する必要がある。
1.1 実験用データ
このプログラムではIrisデータセットが実験用データである。3種のアヤメ(Setosa、Versicolor、Virginica)について、がく片の長さ・幅、花弁の長さ・幅の4つの特徴量を150サンプル(各種50サンプル)収録している。
1.2 実験計画
何を明らかにするために実験を行うのかを定める。
計画例:
- 各特徴量の分布の形状を確認する(正規分布に従うか、偏りがあるか)
- 3種のアヤメを最も区別しやすい特徴量を見つける
- 特徴量間の相関関係を調べる(どの特徴量が互いに関連しているか)
- 外れ値の有無を確認する
- 種間で統計的な差異がある特徴量を特定する
- 2つの特徴量の組み合わせで種を分類できるか確認する
1.3 プログラム
実験を実施するためのツールである。このプログラムはscikit-learnのIrisデータセット、pandas、matplotlib、seabornを使用している。
- プログラムの機能を理解して活用することが基本である
- 基本となるプログラムを出発点として、将来、様々な機能を自分で追加することができる
1.4 プログラムの機能
このプログラムは複数の可視化と統計分析を自動実行する。
入力データ:
- 4つの数値特徴量(がく片の長さ・幅、花弁の長さ・幅)
- 1つのカテゴリ変数(種名:Setosa、Versicolor、Virginica)
出力情報:
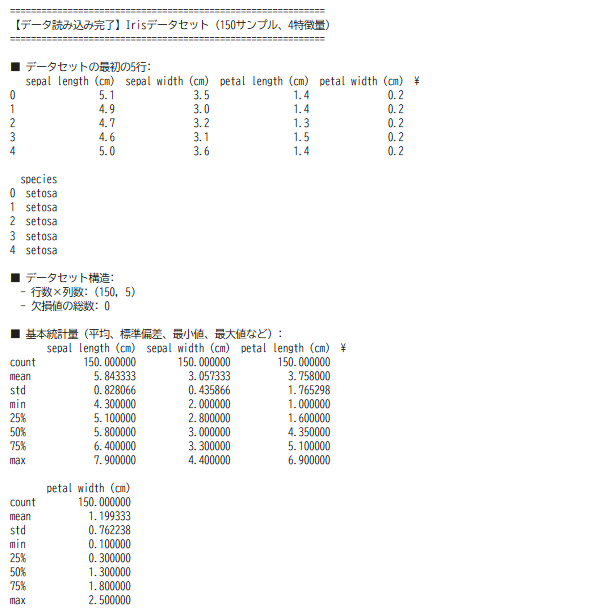
- 基本統計量:平均、標準偏差、最小値、最大値、四分位数
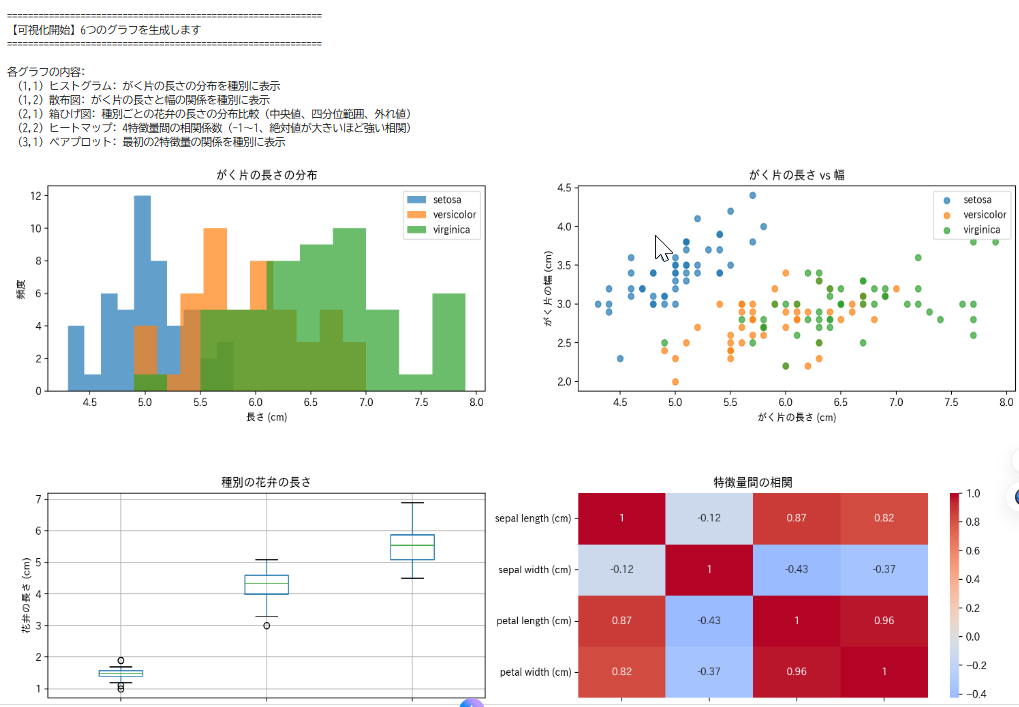
- ヒストグラム:がく片の長さの分布を種別に表示
- 散布図:がく片の長さと幅の関係を種別に表示
- 箱ひげ図:種別ごとの花弁の長さの分布比較(中央値、四分位範囲、外れ値)
- 相関ヒートマップ:4特徴量間の相関係数(-1から1、絶対値が大きいほど強い相関)
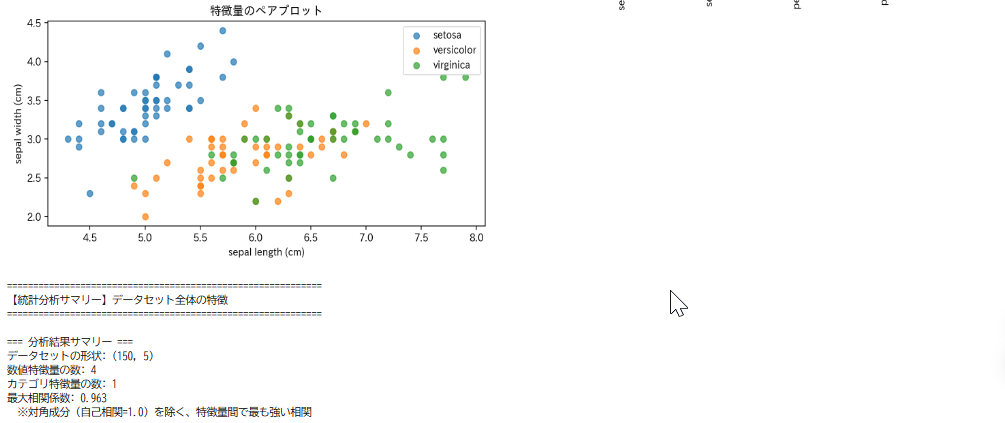
- ペアプロット:最初の2特徴量の関係を種別に表示
データの自動処理:
- データの読み込みと構造確認が自動で行われる
- 欠損値の有無が自動で確認される
- すべてのグラフが一度に生成される
1.5 検証(結果の確認と考察)
プログラムの実行結果を観察し、データの特性を考察する。
基本認識:
- データを複数の視点から見ることで、隠れたパターンや特性が見えてくる
- 研究目的によって興味深い結果は異なる
- 同じデータでも可視化方法を変えると異なる発見がある
観察のポイント:
- 各特徴量の分布は左右対称か、偏っているか
- 3つの種を明確に区別できる特徴量はどれか
- 散布図で種が重なっている領域はあるか
- 箱ひげ図で外れ値は見られるか
- 相関係数が高い特徴量の組み合わせはあるか
- 統計量(平均、標準偏差)は種間でどの程度異なるか
2. 間違いの原因と対処方法
2.1 期待と異なる結果が出る場合
相関係数が1.0
- 原因:対角成分(自己相関)を見ている可能性がある
- 対処方法:対角成分は常に1.0である。それ以外の値に注目する。相関が強いのは0.8以上の値である
散布図で種が完全に分離されていない
- 原因:これは正常な結果である。特にVersicolorとVirginicaは重なる領域がある
- 対処方法:どの特徴量の組み合わせなら分離しやすいか、複数の散布図を比較する。これがデータ分析における重要な気づきである
基本統計量の平均と中央値が大きく異なる
- 原因:データに偏りがある、または外れ値の影響を受けている
- 対処方法:箱ひげ図やヒストグラムで分布の形状を確認する。これはデータの非対称性を示す重要な発見である
3. 実験レポートのサンプル
種を区別する最適な特徴量の探索
実験目的:
Irisデータセットの3種(Setosa、Versicolor、Virginica)を最も明確に区別できる特徴量または特徴量の組み合わせを見つける。
実験計画:
各特徴量について、種間の分離度を評価する。箱ひげ図で種間の重なりを確認し、散布図で2つの特徴量の組み合わせによる分離性を評価する。
実験方法:
プログラムを実行し、生成された6つのグラフを観察しながら以下の基準で評価する:
- 完全分離:3つの種が全く重ならない
- 部分分離:一部の種は区別できるが、他は重なる
- 重複大:種間の重なりが大きく、区別が困難
実験結果:
| 特徴量 | Setosaの分離 | Versicolor/Virginicaの分離 | 総合評価 |
|---|---|---|---|
| がく片の長さ | xxx | xxx | xxx |
| がく片の幅 | xxx | xxx | xxx |
| 花弁の長さ | xxx | xxx | xxx |
| 花弁の幅 | xxx | xxx | xxx |
| 特徴量の組み合わせ | 分離の明確さ | 観察された特徴 |
|---|---|---|
| がく片の長さ × がく片の幅 | xxx | (例文)Setosaは部分的に分離、他2種は重複 |
| 花弁の長さ × 花弁の幅 | xxx | (例文)Setosaは完全分離、他2種も比較的明確 |
考察:
- (例文)花弁の長さと花弁の幅は、単独でも3種を区別する能力が高い。特にSetosaは他の2種と完全に分離している
- (例文)箱ひげ図から、Setosaの花弁の長さはx.x~x.xcm程度で、他の2種(x.xcm以上)と明確に異なることが確認できた
- (例文)相関ヒートマップから、花弁の長さと幅の相関係数がx.xxと高いことが分かった。これは両者が同様の情報を持つことを示している
- (例文)がく片の特徴量だけでは種の判別が困難である。散布図でVersicolorとVirginicaが大きく重なっていた
- (例文)散布図「花弁の長さ × 花弁の幅」では、Setosaが左下に密集し、VersicolorとVirginicaも比較的分離していることが視覚的に確認できた
結論:
(例文)本実験により、Irisデータセットの3種を区別するには花弁の特徴量(長さ・幅)が最も有効であることが確認できた。特にSetosaは花弁が小さいという明確な特徴を持つため、他の2種と容易に区別できる。VersicolorとVirginicaの区別には複数の特徴量を組み合わせる必要があるが、花弁の長さがx.xcm未満ならSetosa、x.x~x.xcm程度ならVersicolor、x.xcm以上ならVirginicaという大まかな分類基準を設定できる。この知見は機械学習による分類モデルの特徴量選択にも活用できる。
![[kaneko lab.]](https://www.kkaneko.jp/info/logo_png.png)