表形式データの処理と分析:DataFrame操作、欠損値処理、統計量算出、可視化
【概要】本記事では、pandas DataFrameを用いた表形式データの基本的な処理と分析手法を解説する。CSVファイルからのデータ読み込み、データ構造の確認、欠損値の検出と処理、カテゴリ変数の数値化、基本統計量の算出、ヒストグラムによる可視化、グループ別集計までの一連の処理を、学生データを題材として実践的に学習する。データ分析の初学者がpandasとmatplotlibの基本操作を習得するための教材である。
Colab のページ(ソースコードと説明): https://colab.research.google.com/drive/1gafrOx5HrepqtUbspUIFKeD_obE6of1u?usp=sharing


【目次】
用語リスト
-
DataFrameの理解
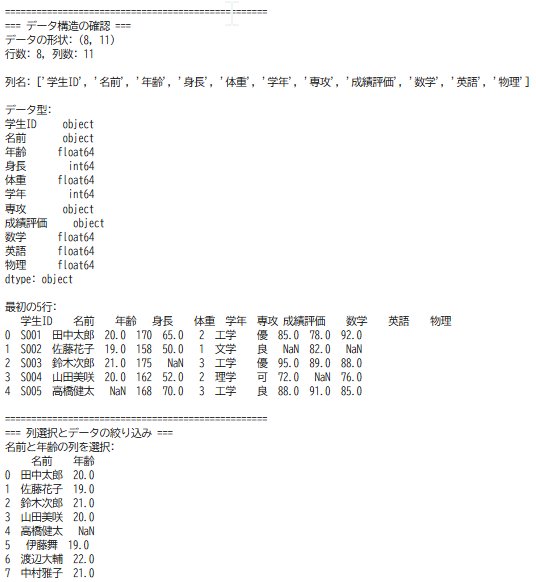
表形式のデータ構造で、行(レコード)と列(カラム)で構成される。大量データの場合、構造を把握する必要がある。
-
データの選択と絞り込み
特定の列や条件に合うデータのみを扱うことで、必要な情報だけを効率的に取り出すことができる。
-
欠損値の存在
現実のデータには欠損値が存在する。欠損値を無視して分析を行うと、誤った結論に至る危険性がある。
-
欠損値の処理戦略
削除は最も基本的で理解しやすい処理方法である。削除による影響(失われるデータの量と性質)を確認する必要がある。
-
カテゴリ変数の数値化
コンピュータは数値データの方が文字列データよりも効率的に処理できる。統計分析や機械学習では、文字列で表現されたカテゴリを数値に変換する必要がある。
-
基本統計量の算出
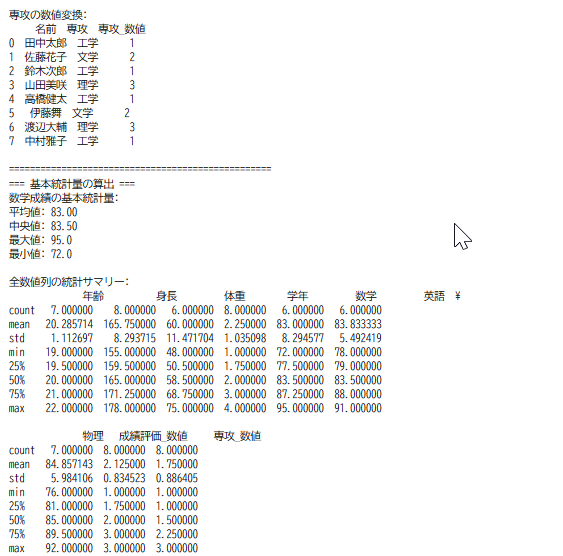
平均値、中央値、最大値、最小値などの基本統計量を算出する。describe()関数で全数値列の統計サマリーを一度に取得できる。
-
PythonとExcelの使い分け
Pythonは大量データの高速処理、自動化、再現性に優れている。Excelは少量データの視覚的操作、直感的理解に適している。
-
データ可視化の役割
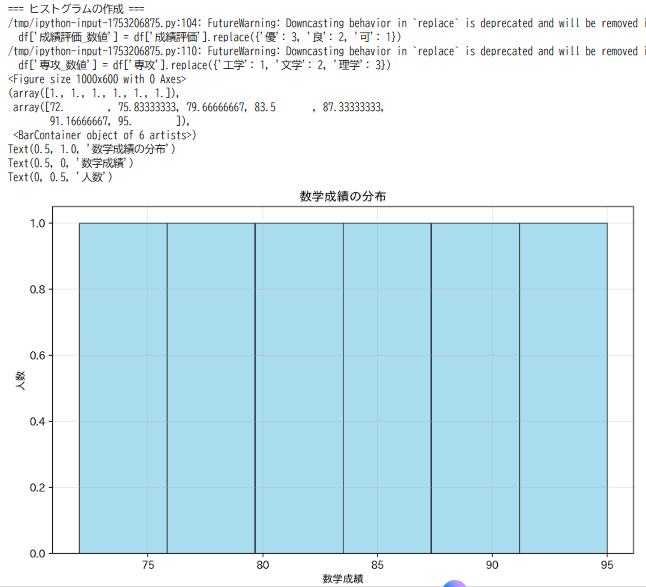
数値だけでは見づらいデータの特徴をグラフによって視覚的に理解できる。ヒストグラムは数値データの分布(散らばり具合)を把握する基本的な手法である。
-
グループ別の集計
groupby()を用いてカテゴリ別の統計量を算出する。専攻別の平均成績など、グループごとの傾向を把握できる。
プログラム利用ガイド
1. このプログラムの利用シーン
表形式データの基本的な処理と分析を学習する教育場面で利用する。サンプルデータを題材に、データの読み込み、構造確認、欠損値処理、統計量算出、可視化までの一連の流れを習得できる。データ分析の初学者がpandasとmatplotlibの基本操作を理解するためのプログラムである。
2. 主な機能
本プログラムは、データ構造の確認として、行数、列数、列名、データ型、最初の数行を表示し、データ全体の構造を把握する機能を提供する。列選択とデータ絞り込みでは、特定の列を選択し、条件に合致する行のみを抽出する。欠損値の検出と処理では、欠損値の個数と位置を確認し、欠損値を含む行を削除する。カテゴリ変数の数値化では、文字列で表現された成績評価や専攻を数値に変換する。基本統計量の算出では、平均値、中央値、最大値、最小値などの統計量を計算する。ヒストグラムの作成では、数値データの分布をヒストグラムで可視化する。グループ別集計では、専攻別など、カテゴリごとの統計量を算出する。
3. 基本的な使い方
まず、Colabのページを開く。Colabのページ(ソースコードと説明): https://colab.research.google.com/drive/1gafrOx5HrepqtUbspUIFKeD_obE6of1u?usp=sharing。次に、セルを実行する。データの確認では、出力結果を確認しながら、処理内容を理解する。パラメータの変更では、ヒストグラムのビン数や色などのパラメータを変更し、結果の違いを観察する。
プログラムの説明
概要
このプログラムは、学生データを用いてpandas DataFrameの基本操作、欠損値処理、統計量算出、データ可視化を実践する教育用プログラムである。CSVファイルから表形式データを読み込み、データ構造の確認、列の選択と絞り込み、欠損値の検出と削除、カテゴリ変数の数値化、基本統計量の算出、ヒストグラムによる可視化、グループ別集計までの一連の処理を実行する[1]。
主要技術
pandas DataFrame
pandasライブラリが提供する2次元の表形式データ構造である[1]。行(レコード)と列(カラム)で構成される。各列は異なるデータ型を持つことができる。大量データの読み込み、選択、フィルタリング、集計などの操作を行う[1][2]。
matplotlib
Pythonのプロット作成ライブラリである[3]。pyplot.hist()関数を用いてヒストグラムを作成する。データの分布を視覚的に表現し、ビン数、色、透明度などのパラメータを調整できる[3]。
技術的特徴
欠損値の検出と処理
isnull()メソッドで欠損値(NaN)を検出する。欠損値の個数と位置を確認できる[1]。dropna()メソッドで欠損値を含む行を削除する。subsetパラメータを指定すれば、特定列の欠損値のみを対象とした処理も可能である[1]。
カテゴリ変数の数値変換
replace()メソッドを用いて、文字列で表現されたカテゴリ(「優」「良」「可」など)を数値に変換する[1]。文字列データを数値データに変換することで、統計計算や機械学習アルゴリズムへの入力として利用できる。
基本統計量の算出
mean()、median()、max()、min()などのメソッドで各列の統計量を算出する[1]。describe()メソッドは、全数値列の平均値、標準偏差、最小値、四分位数、最大値を一度に取得する[1]。
グループ別集計
groupby()メソッドを用いてカテゴリ別にデータを分割する。各グループの統計量を算出できる[1]。split-apply-combineの処理パターンにより、専攻別の平均成績などグループごとの傾向を把握する[1]。
実装の特色
段階的な学習構成により、データ構造の確認から可視化まで順を追って理解できる構造である。複数の可視化例(数学成績のヒストグラム、身長のヒストグラム)により、同じ手法の異なるデータへの適用を示している。
参考文献
[1] pandas development team. (n.d.). pandas documentation. https://pandas.pydata.org/docs/
[2] McKinney, W. (2010). Data Structures for Statistical Computing in Python. Proceedings of the 9th Python in Science Conference, 56-61.
[3] Hunter, J. D. (2007). Matplotlib: A 2D graphics environment. Computing in Science & Engineering, 9(3), 90-95. https://matplotlib.org/
実験・研究スキルの基礎:Google Colabで学ぶデータ分析実験
1. 実験・研究のスキル構成要素
実験や研究を行うには、以下の5つの構成要素を理解する必要がある。
1.1 実験用データ
このプログラムではCSVファイル(student_data.csv)が実験用データである。8名の学生情報を含み、年齢、身長、体重、成績などのデータが記録されている。データには意図的に欠損値が含まれており、現実のデータの特性を反映している。
1.2 実験計画
何を明らかにするために実験を行うのかを定める。計画例として、ヒストグラムのビン数が分布の見え方に与える影響を確認する、欠損値の削除方法(全体削除、特定列のみ削除)が統計量に与える影響を比較する、専攻別の成績傾向を明らかにする、欠損値を含むデータと削除後のデータで平均値がどう変化するかを調べる、身長と体重の分布パターンの違いを可視化によって確認する、などが挙げられる。
1.3 プログラム
実験を実施するためのツールである。このプログラムはpandasとmatplotlibライブラリを使用している。プログラムの機能を理解して活用することが基本である。基本となるプログラムを出発点として、将来、様々な分析機能を自分で追加することができる。
1.4 プログラムの機能
このプログラムは表形式データの基本的な処理と分析を行う。
入力パラメータ(変更可能な要素)として、ヒストグラムのビン数(bins)はデータを何個の区間に分割するか(例:6、8、10)を指定する。欠損値処理の対象列(subset)はどの列の欠損値を削除対象とするかを指定する。グループ化の基準列はどの列でデータをグループ分けするか(例:専攻、学年)を指定する。
出力情報として、データの形状(行数、列数)、欠損値の個数と位置、基本統計量(平均値、中央値、最大値、最小値)、ヒストグラム(データ分布の視覚化)、グループ別の統計量(専攻別の平均成績など)が得られる。
処理の流れは、データ読み込み、構造確認、欠損値確認、統計量算出、可視化、グループ別集計の順で進行する。
1.5 検証(結果の確認と考察)
プログラムの実行結果を観察し、パラメータの影響やデータの特性を考察する。
基本認識として、パラメータを変えると結果が変わる。その変化を観察することが実験である。欠損値の処理方法によって統計量は変化する。どの方法が適切かはデータと目的による。データの可視化により、数値だけでは見えない特徴やパターンを発見できる。
観察のポイントとして、欠損値はどの列にどれだけ存在するか、欠損値を削除すると何行のデータが失われるか、欠損値削除前後で平均値や中央値はどう変化するか、ヒストグラムのビン数を変えると分布の見え方はどう変わるか、グループ間で統計量に明確な差が見られるか、などを確認する。
2. 間違いの原因と対処方法
2.1 プログラムのミス(人為的エラー)
統計量が表示されない(NaNと表示される)場合、原因は対象列に欠損値が含まれていることである。対処方法として、これは正常な動作である。欠損値を含む列の統計量は計算できないため、欠損値処理が必要であることを理解する。
2.2 期待と異なる結果が出る場合
平均値と中央値が大きく異なる場合、原因はデータに極端な値(外れ値)が含まれている、またはデータが偏った分布をしていることである。対処方法として、これは正常な現象である。平均値は外れ値の影響を受けやすいが、中央値は影響を受けにくい。ヒストグラムで分布を確認し、どちらの統計量が適切かを判断する。
欠損値を削除すると大部分のデータが失われる場合、原因は多くの行に欠損値が含まれていることである。対処方法として、dropna(subset=['列名'])を使用し、分析に必要な特定の列のみを対象として欠損値を削除する。全列を対象とすると過度にデータが失われる可能性がある。
ヒストグラムの形が滑らかでない場合、原因はビン数が少なすぎる、またはデータ数が少ないことである。対処方法として、bins=10やbins=15のように値を変更して、分布の特徴が適切に表現される設定を探す。データ数が少ない場合は、ビン数を減らす方が適切である。
グループ別の統計量に差が見られない場合、原因はグループ間の差が実際に小さい、またはデータ数が少なすぎることである。対処方法として、これは重要な発見である。「差がない」という結果も実験結果として記録する。別の列でグループ化を試みることも有効である。
3. 実験レポートのサンプル
ヒストグラムのビン数が分布解釈に与える影響
実験目的は、数学成績のヒストグラムにおいて、ビン数が分布の見え方と解釈にどのような影響を与えるかを明らかにすることである。
実験計画として、同じ数学成績データに対して、ビン数を3、6、12と変化させてヒストグラムを作成し、それぞれの分布の見え方を比較する。
実験方法として、プログラムのヒストグラム作成部分で、binsパラメータを変更しながら実行し、分布の形状(データの散らばり具合が把握できるか)、特徴の識別(ピークや偏りが明確に見えるか)、解釈のしやすさ(結果から傾向を読み取りやすいか)の基準で評価する。
実験結果(記載例)として、以下の表にまとめる。
| ビン数 | 観察された特徴 | 長所 | 短所 | 総合評価 |
|---|---|---|---|---|
| 3 | (記載例)大まかな分布のみ | (記載例)全体像を素早く把握 | (記載例)詳細な分布が不明 | (記載例)△ |
| 6 | (記載例)適度な粒度で分布が見える | (記載例)バランスが良い | (記載例)特になし | (記載例)◎ |
| 12 | (記載例)細かすぎて不規則 | (記載例)詳細な分析が可能 | (記載例)データ数が少ないと不安定 | (記載例)△ |
考察:
(例文)ビン数3では、xxx点台とxxx点台の違いが区別できず、「成績が良い学生が多い」という大雑把な情報しか得られなかった。
(例文)ビン数6では、成績分布の偏りやピークの位置が適切に可視化され、「xxx点前後に集中している」という具体的な傾向が読み取れた。
(例文)ビン数12では、データ数がxxx件と少ないため、各ビンの度数が0または1となり、分布が不規則に見えた。データ数に対してビン数が多すぎると解釈が困難になることが確認できた。
(例文)ビン数は「多ければ良い」わけではなく、データ数に応じた適切な設定が必要であることが明らかになった。
結論:
(例文)本実験では、ビン数6が最も適切であった。データ数が少ない場合、ビン数を増やしすぎると分布が不安定になり、解釈が困難になる。一般的な目安として、データ数がxxx件程度の場合はビン数xxxからxxx程度、データ数がxxx件を超える場合はビン数xxxからxxx程度が適切である。ヒストグラムの作成では、必ず複数のビン数を試し、最も分布の特徴を適切に表現する設定を選択する必要がある。
欠損値処理方法が統計量に与える影響
実験目的は、欠損値を含むデータにおいて、処理方法(全削除、特定列のみ削除、削除なし)が統計量にどのような影響を与えるかを定量的に比較することである。
実験計画として、数学成績データに対して3つの処理方法を適用し、それぞれの平均値、中央値、データ数を比較する。
実験方法として、条件A(欠損値削除なし、元データをそのまま使用)、条件B(全列の欠損値削除、dropna())、条件C(数学列のみの欠損値削除、dropna(subset=['数学']))の3つの条件でデータを処理し、統計量を記録する。
実験結果(記載例)として、以下の表にまとめる。
| 処理方法 | データ数 | 平均値 | 中央値 | 失われたデータ数 |
|---|---|---|---|---|
| 条件A(削除なし) | (記載例)8件 | (記載例)83.7点 | (記載例)85.0点 | (記載例)0件 |
| 条件B(全削除) | (記載例)3件 | (記載例)85.0点 | (記載例)85.0点 | (記載例)5件 |
| 条件C(数学のみ) | (記載例)6件 | (記載例)83.7点 | (記載例)85.0点 | (記載例)2件 |
考察:
(例文)条件Aでは全データを保持できるが、欠損値を含む行が計算に影響しないため、実質的には条件Cと同じ結果となった。pandasのmean()は欠損値を自動的に除外して計算する。
(例文)条件Bでは、他の列(年齢、身長など)に欠損値がある行もすべて削除されるため、xxx件中xxx件が失われ、わずかxxx件のデータしか残らなかった。これでは統計的な信頼性が著しく低下する。
(例文)条件Cでは、数学成績に欠損値があるxxx件のみが削除され、xxx件のデータで分析できた。分析対象の列のみに焦点を当てることで、適切なデータ数を確保できた。
(例文)平均値と中央値がほぼ同じ値を示しており、データに極端な外れ値がないことが確認できた。
結論:
(例文)欠損値処理では、分析に必要な列のみを対象として削除する方法(条件C)が最も適切であった。全列を対象とすると過度にデータが失われ、統計的な信頼性が損なわれる。現実のデータ分析では、「どのデータを残し、どのデータを削除するか」という判断が分析結果に大きく影響する。欠損値処理は機械的に行うのではなく、分析目的とデータの特性を考慮して慎重に決定する必要がある。
![[kaneko lab.]](https://www.kkaneko.jp/info/logo_png.png)