Octaveによる数値計算とデータ処理の基礎

【要点】

変数 M に2行2列の行列を格納する場合、次のような記法を使用する。

M = [1 3; 2 4]

この行列は次のように配置される。

1 3
2 4

• 行列のコンストラクタ

  各行を「;」（セミコロン）で区切って記述する。

  A = [1 2 3; 4 5 6]
  

• 全要素が 0 の行列: zeros関数

  「zeros(n, m)」と記述する。nは行数、mは列数を表す。

  A = zeros(3, 4)
  

• 全要素が 1 の行列: ones関数

  「ones(n, m)」と記述する。nは行数、mは列数を表す。

  A = ones(3, 4)
  

• 全要素が同じ値の行列

  「zeros(n, m) + x」と記述する。nは行数、mは列数、xは設定したい値を表す。

  A = zeros(3, 4) + 5
  

• 単位行列: eye関数

  「eye(n)」と記述する。nは行数（および列数）を表す。単位行列は正方行列（行数と列数が等しい行列）である。

  A = eye(3)
  

• 対角行列: diag関数

  引数として指定したベクトルの要素が対角要素となる行列を生成する。

  A = diag([1 2 3 4])
  

• 0 から 1 の一様乱数を要素に持つ行列: rand関数

  「rand(n, m)」と記述する。nは行数、mは列数を表す。

  x = rand(3, 4)
  

• 平均 0、分散 1 の正規分布の乱数を要素に持つ行列: randn関数

  「randn(n, m)」と記述する。nは行数、mは列数を表す。

  x = randn(3, 4)
  

• ベクトルを行列に変換: reshape関数

  「reshape(v, n, m)」と記述する。vはベクトル、nは行数、mは列数を表す。

  
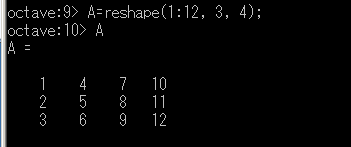
• メッシュグリッド: meshgrid関数

  座標値のベクトルからメッシュグリッドを生成する。

  [XX, YY] = meshgrid([0 1 2 3], [1 2 3])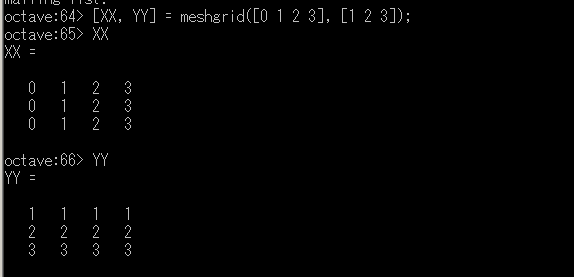
  

  

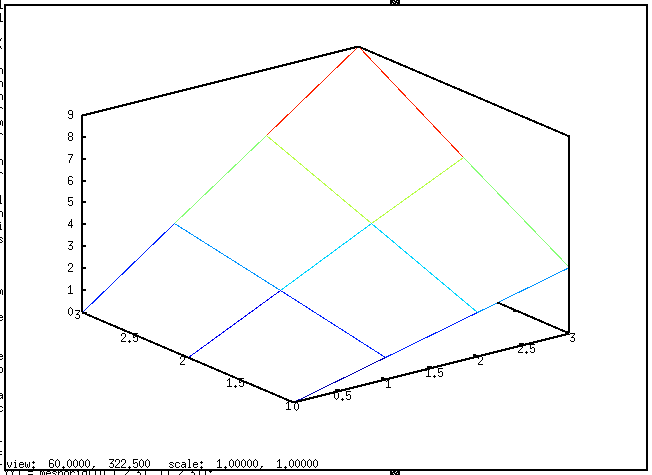
  使用例として、mesh関数による3次元表示を示す。

  x = [0 1 2 3];
  y = [1 2 3];
  [XX, YY] = meshgrid(x, y);
  ZZ = XX.*YY;
  mesh(XX, YY, ZZ);
  close;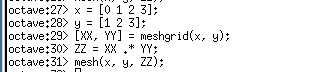
  

  

  

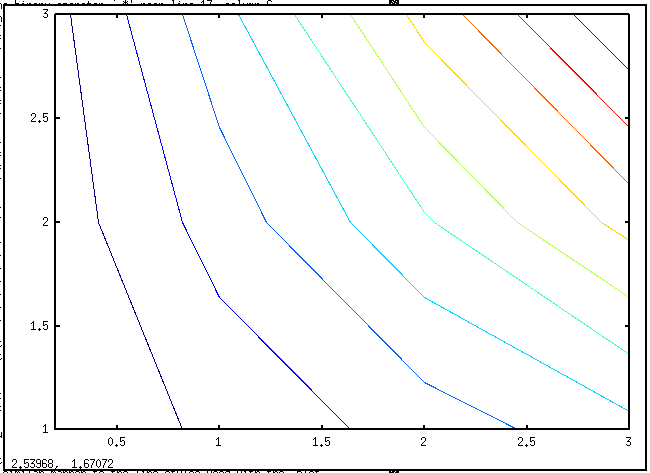
  使用例として、contour関数による等高線表示を示す。

  x = [0 1 2 3];
  y = [1 2 3];
  [XX, YY] = meshgrid(x, y);
  ZZ = XX.*YY;
  contour(XX, YY, ZZ);
  close;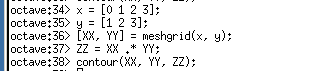
  

  

  

• 空行列／空ベクトル []

行列の要素の操作

• 参照（行列→行列、行ベクトル、列ベクトル、スカラー）
  • 参照時は、行番号と列番号をカンマで区切って指定する。

    A = [1 2 3 4; 5 6 7 8; 9 10 11 12]
    A(1, 1)
    A(3, 2)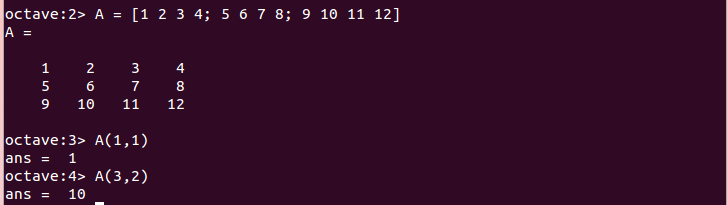
    

    
  • 範囲指定には「:」（コロン）を使用する。「2:4」は行ベクトル[2 3 4]を表す。「:」単独では、全ての行または全ての列を意味する。

    A = [1 2 3 4; 5 6 7 8; 9 10 11 12]
    A(1:2, 2:4)
    A(1:2, 2)
    A(1:2, :)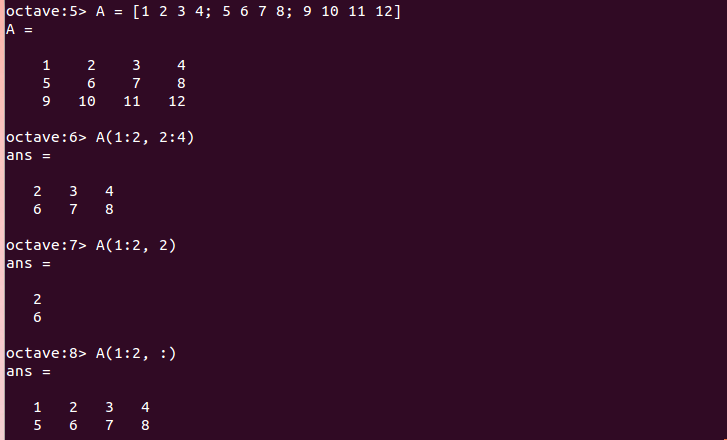
    

    
  • 行番号や列番号はベクトルでの指定も可能である。

    A(1:2, [2 4])
    

• 条件に合致する行の選択

  X = [1 102; 1 102; 2 101; 3 101; 3 103]
  X(:, 1) == 3
  X( X(:, 1) == 3, : )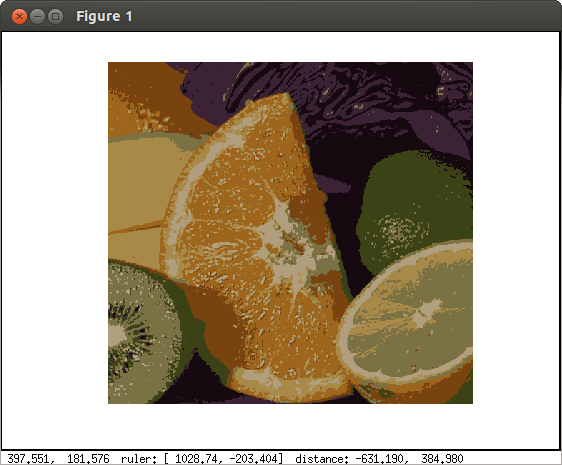
  

  
• 要素の代入

  A = [1 2 3 4; 5 6 7 8; 9 10 11 12]
  A(2, 3) = 60
  A
  

• 行の追加

  同じ列数の行ベクトルまたは行列を連結する。以下の例では、A の後に「;」（セミコロン）を配置する。

  A = [1 2 3 4; 5 6 7 8; 9 10 11 12]
  B = [A; [13 14 15 16]]
  C = [A; [13 14 15 16; 17 18 19 20]]
  

• 列の追加

  同じ行数の列ベクトルまたは行列を連結する。半角スペースで区切って連結したい行列や列ベクトルを並べる。

  A = [1 2 3 4; 5 6 7 8; 9 10 11 12]
  B = [A [100; 101; 102]]
  C = [A [100 200; 101 201; 102 202]]
  

• 行列の連結

  行方向の連結には「;」（セミコロン）を使用する。

  A = [1 2 3 4; 5 6 7 8; 9 10 11 12]
  D = [13 14 15 16; 17 18 19 20]
  [A; D]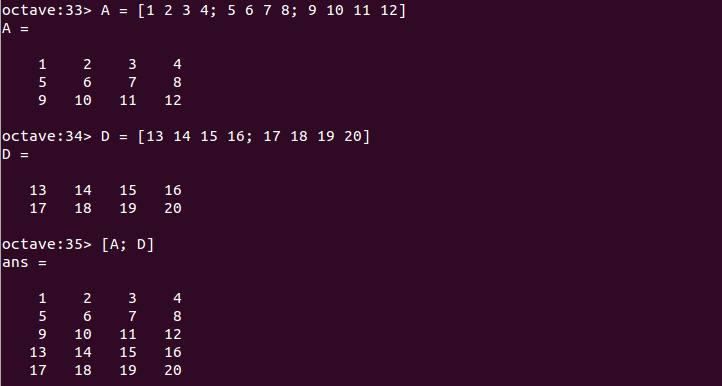
  

  

  列方向の連結には半角スペースを使用する。

  A = [1 2 3 4; 5 6 7 8; 9 10 11 12]
  E = [20 21; 22 23; 24 25]
  [A E]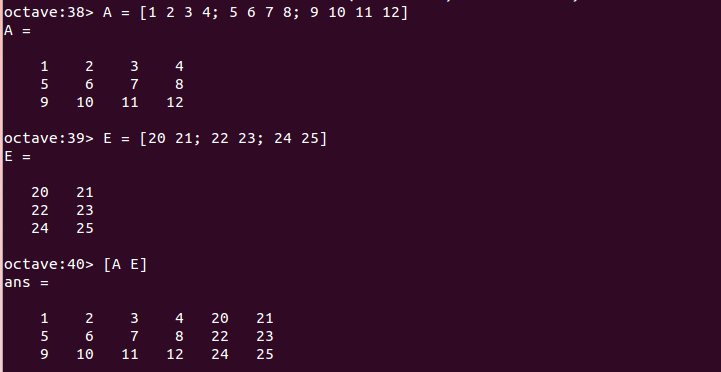
  

  
• 行の削除

  空行列 [] を使用して削除を行う。

  A = [1 2 3 4; 5 6 7 8; 9 10 11 12]
  A([1 3], :) = []
  A
  

• 列の削除

  空行列 [] を使用して削除を行う。

  A = [1 2 3 4; 5 6 7 8; 9 10 11 12]
  A(:, [1 3]) = []
  A
  

行列の演算

• 行列の要素のデータ型： class関数
  
• 次元の取得： ndims関数

  ベクトルの場合は1、行列の場合は2を返す。

• サイズ： size関数

  行列の行数と列数はそれぞれ次のコマンドで取得できる。

  size(mat, 1)
  size(mat, 2)
  

• 転置（行列 → 行列）

  「.'」演算子による転置、「'」演算子による複素共役転置がある。

  A = [1 2 3; 4 5 6]
  A.'
  A'
  

• 行列に同じ数を足す： +演算子
  
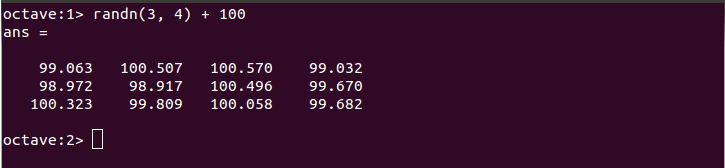
  行列に同じ数を足す
• 行列の定数倍： *演算子
• 行列と特定の値との比較： ==演算子

  X = [1 2 3; 2 3 2; 2 2 3]
  X == 2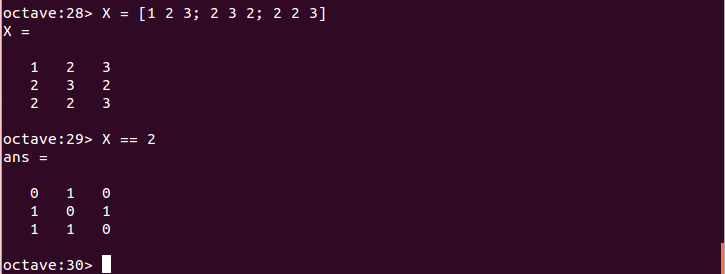
  

  
• 行列とベクトルの積、行列と行列の積: *演算子
  
  行列とベクトルの積
  
  行列と行列の積
• 除算（左除算）： \演算子

  A\y は、連立方程式 Ax = y の解 x を求める演算である。A\Y は、行列方程式 A*X = Y の解行列 X を求める。

• 除算（右除算）： /演算子

  A/Y = (Y'\A')' と定義される。A/Y は、行列方程式 X*A = Y の解行列 X を求める。

• 逆行列： inv関数
  
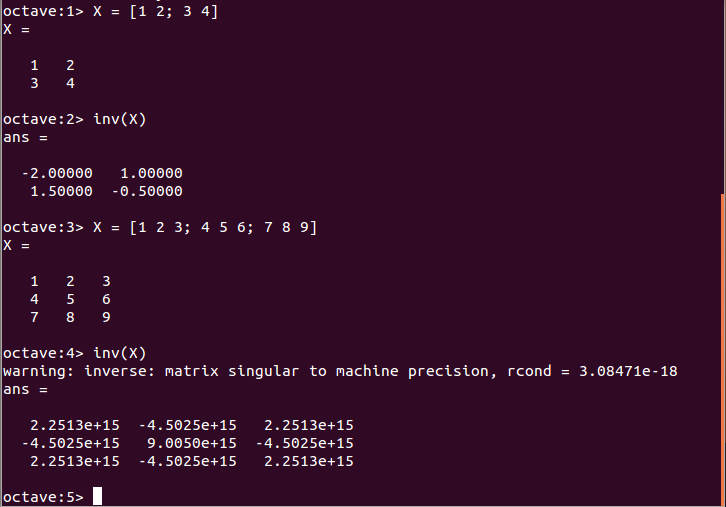
  逆行列の例
• 固有値と固有ベクトル： eig関数
  • 固有値のみを計算する場合: LAMBDA = eig(A)
    
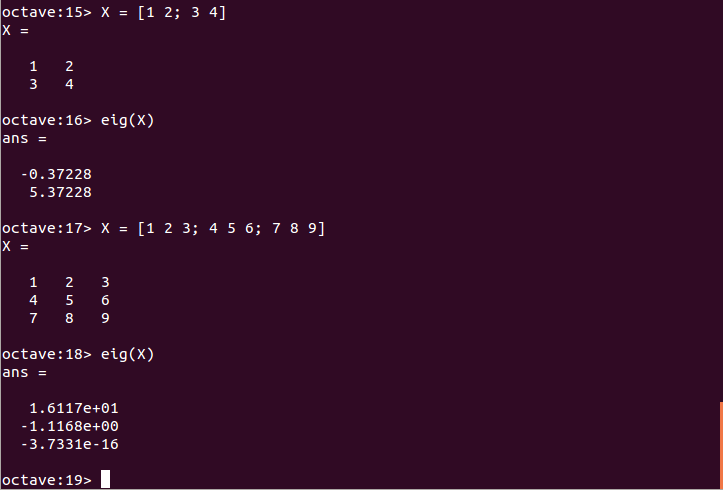
    固有値の例
  • 固有値と固有ベクトルを同時に計算する場合: [V, LAMBDA] = eig(A)

    固有ベクトルは行列Vの列ベクトルとして、固有値は行列LAMBDAの対角要素として得られる。これらは A * V = V * LAMBDA の関係を満たす。

    
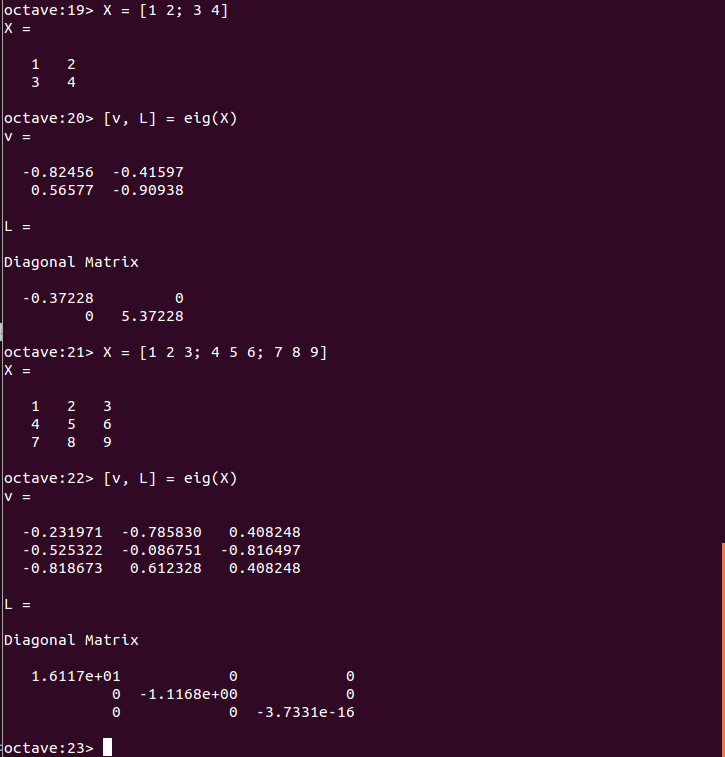
    固有値と固有ベクトルの例
• 行列式： det関数
  
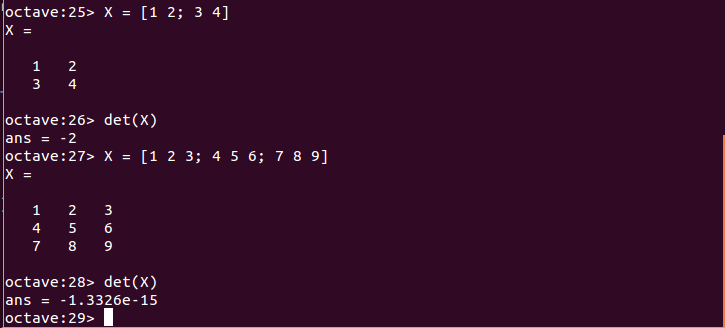
  行列式の例
• 行列のトレース： trace関数

  対角要素の和を計算する。

  X = [1 2 3; 4 5 6; 7 8 9]
  trace(X)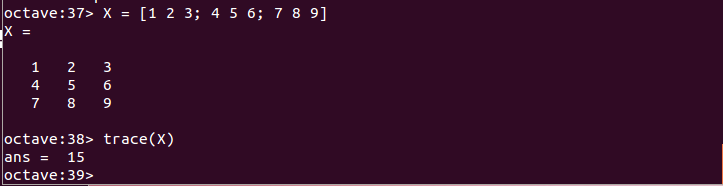
  

  
• 特異値分解（Singular Value Decomposition、SVD）: svd関数

  X = [1 2 3; 4 5 6; 7 8 9]
  [U, S, V] = svd(X)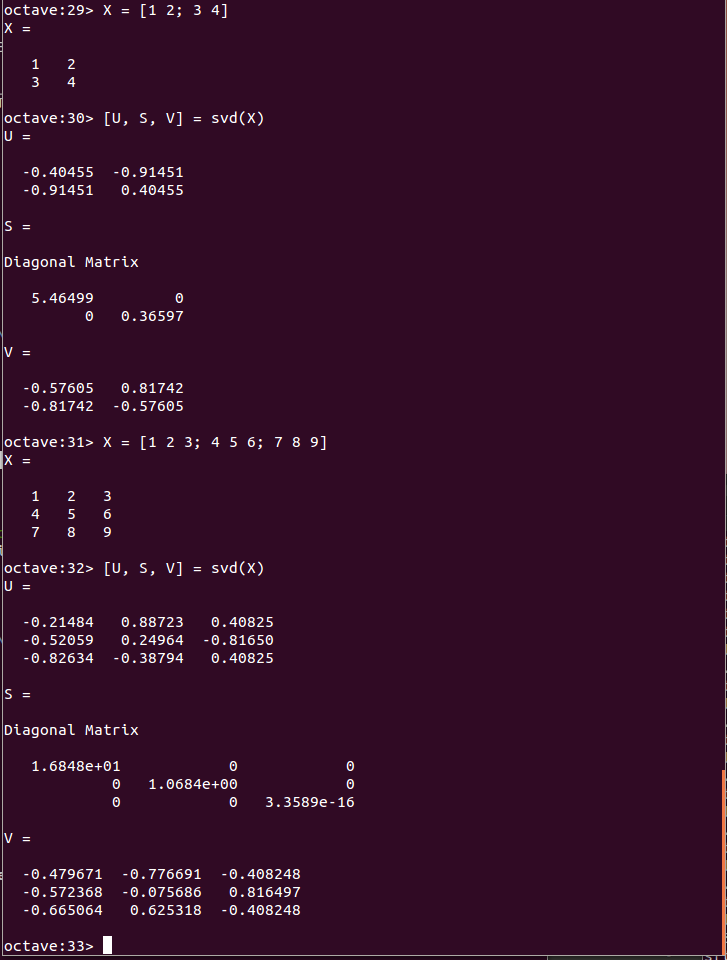
  

  
• LU分解： lu関数

  x = rand(2000, 2000);
  [L, U, P] = lu(x);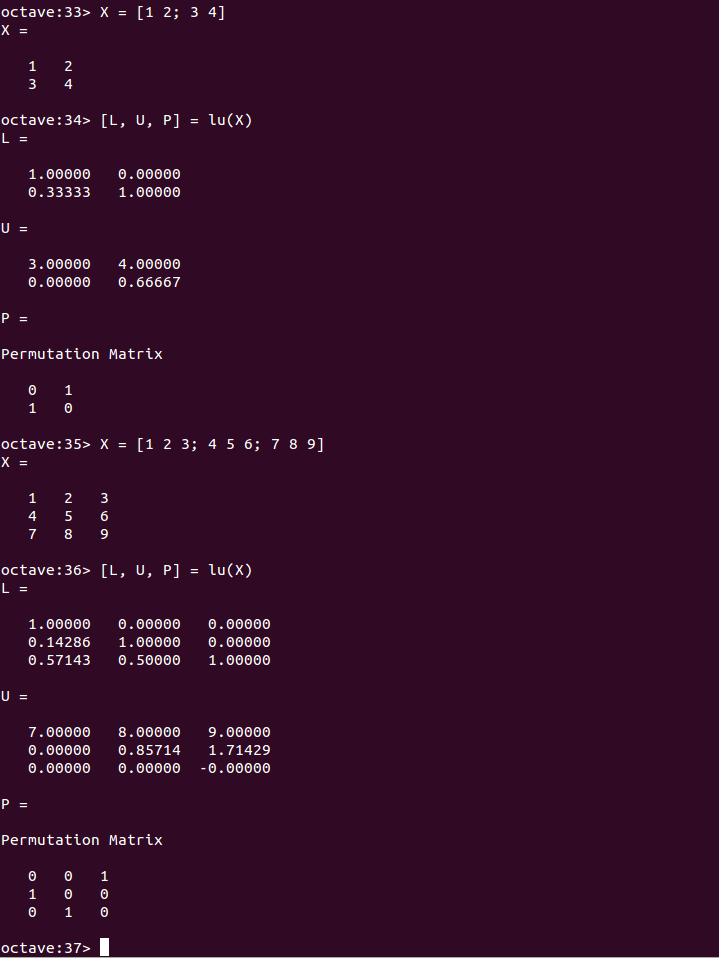
  

  
  LU分解の例
• 行列のランク： rank関数

  非ゼロの特異値の個数を計算する。

  X = [1 2 3; 4 5 6; 7 8 9]
  rank(X)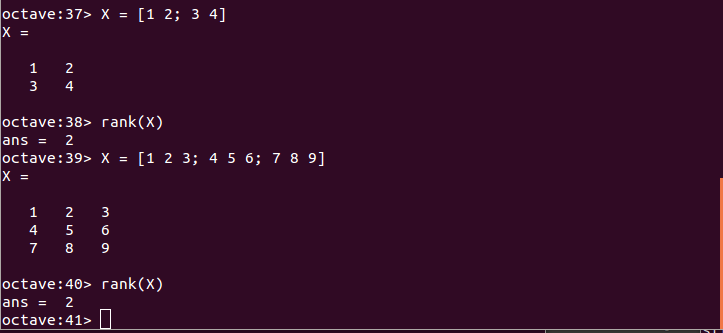
  

  
• QR分解（QR factorization）: qr関数

  X = [1 2 3; 4 5 6; 7 8 9]
  [Q, R, P] = qr(X)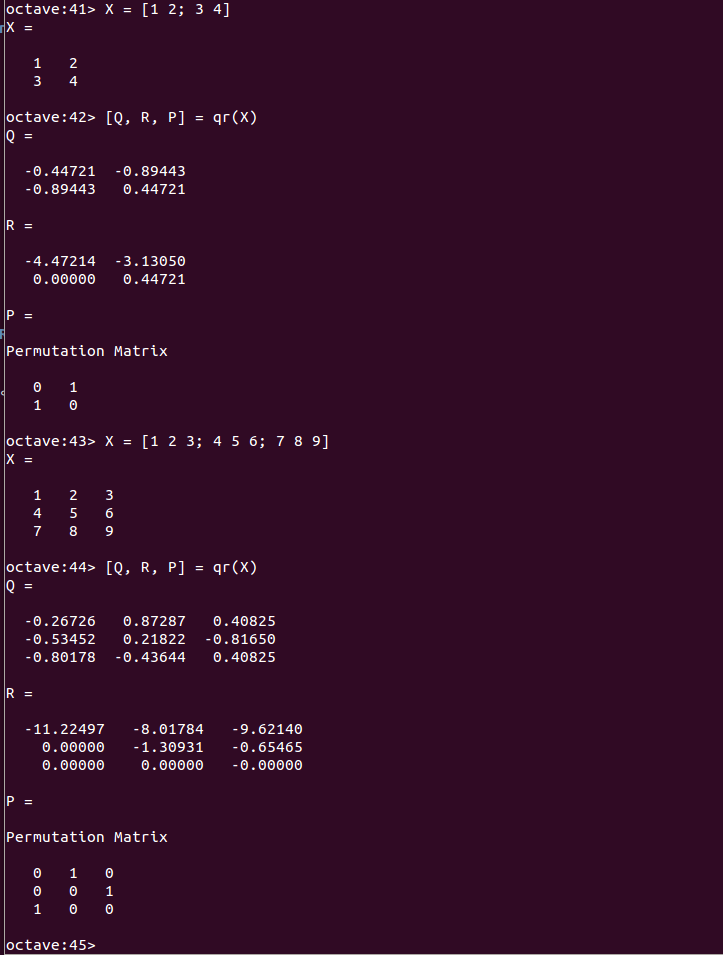
  

  
• 分散共分散行列: cov関数

  X = [11 12 13; 14 15 16; 19 18 17]
  cov(X)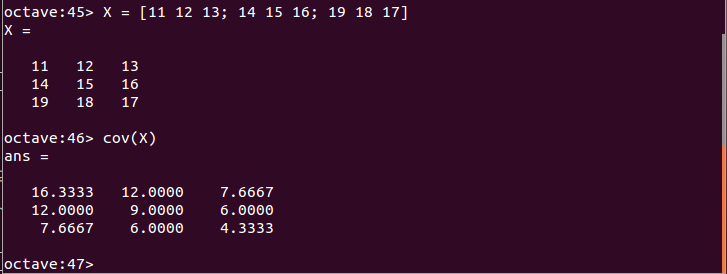
  

  
• 2次元のコンボリューション: conv2関数

  X = [1 2 3; 4 5 6; 7 8 9]
  B = [1 2; 3 4]
  Z = conv2(X, B, 'full')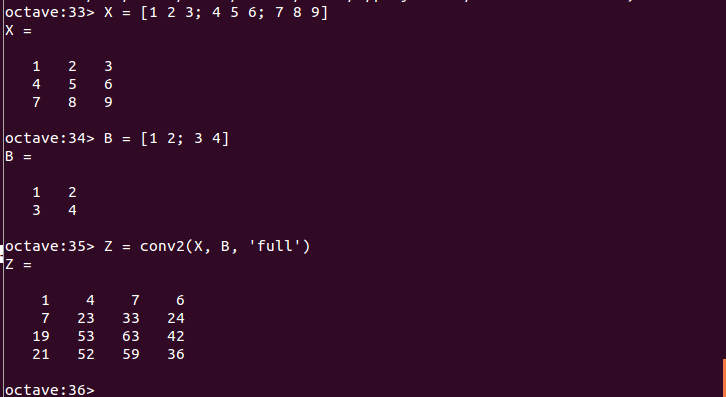
  

  

スカラーに対する演算

Octaveでは，スカラーに対する演算を行列やベクトル（行ベクトルと列ベクトル）に適用できる． この場合，行列やベクトルの各要素に対して個別に演算が実行される． また，同じサイズの行列やベクトル同士であれば2項演算を適用できる．

四則演算

• 和： +
• 差： -
• 積： .*

  行列やベクトルの各要素同士の積を計算する場合は.*演算子を使用する．

• 商： ./

  行列やベクトルの各要素同士の商を計算する場合は./演算子を使用する．

  t = [0.01:0.01:40.96]; plot( sin(t) ./ t );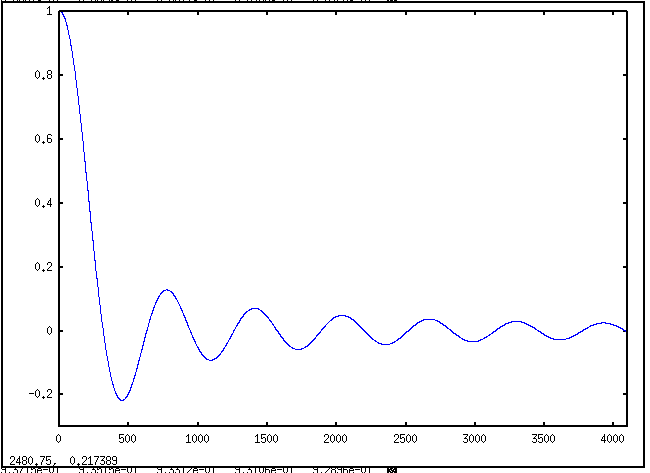
  
• 剰余： mod

数学関数

• べき乗： ^
• 平方根： sqrt
• 絶対値： abs
• 偏角： angle
• 複素数の実部： real
• 複素数の虚部： imag
• 複素共役： conj
• 符号： sign
• 四捨五入： round
• 小数点以下切り捨て： fix
• 床関数： floor
• 天井関数： ceil
• 指数関数（eのべき乗）： exp
• 自然対数： log
• 2を底とする対数： log2
• 10を底とする対数： log10
• サイン関数： sin
• コサイン関数： cos
• タンジェント関数： tan
• 逆サイン関数： asin
• 逆コサイン関数： acos
• 逆タンジェント関数： atan
• 2引数逆タンジェント関数： atan2

  atan2(Y, X)は，(Y/X)の逆タンジェントを計算する．座標平面上の点(X, Y)の偏角を求める際に使用する．

• ベッセル関数： bessel
• ガンマ関数： gamma

論理演算

論理演算では，0を偽（FALSE），0以外の値を真（TRUE）として扱う． 比較演算の結果は，真の場合は1，偽の場合は0となる．

• 論理積（AND）： &
• 論理和（OR）： |
• 否定（NOT）： ~

比較演算

行列やベクトルに対する比較演算は，各要素に対して個別に実行される． 比較結果は，真の場合は1，偽の場合は0となる．

• より小さい： <
• 以下： <=
• より大きい： >
• 以上： >=
• 等しい： ==
• 等しくない： ~=

集約演算

• 最大値： max

  行ベクトルからスカラー値を返す，または行列から各列の最大値を要素とする行ベクトルを返す．

• 最小値： min

  行ベクトルからスカラー値を返す，または行列から各列の最小値を要素とする行ベクトルを返す．

• 平均値： mean

  行ベクトルからスカラー値を返す，または行列から各列の平均値を要素とする行ベクトルを返す．

• 総和： sum

  行ベクトルからスカラー値を返す，または行列から各列の総和を要素とする行ベクトルを返す．

• 要素数： length

  ベクトルの要素数を返す，または行列の最大次元のサイズを返す．

集約演算の使用例を以下に示す．

x = [1 2 3 4 5 6];
max(x)
min(x)
mean(x)
sum(x)
length(x)

グラフ描画関数

• plot：2次元プロットの描画
• plot3：3次元プロットの描画
• view：3次元プロットの視点設定
• title：グラフタイトルの設定
• xlabel：x軸ラベルの設定
• ylabel：y軸ラベルの設定
• zlabel：z軸ラベルの設定
• axis：グラフ範囲の指定
• grid：グリッド線の表示制御
• legend：凡例の表示
• hist：ヒストグラムの描画

  度数分布のヒストグラムデータのみを取得する場合はhistc関数を使用する．

  ヒストグラム描画例を以下に示す．区間の中央値を[-4 -3 -2 -1 0 1 2 3]とする．

  v = randn(1, 2000);
  hist( v, [-4 -3 -2 -1 0 1 2 3] );
  close;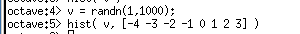
  

  

  

• hist2d：2次元ヒストグラムの描画
• ginput：マウスによる座標入力

その他の関数

最適化関数

• fmin：1変数関数の最小値探索

  使用前にpkg load optimを実行する必要がある．

• fzero：1変数関数の零点探索

  使用前にpkg load optimを実行する必要がある．

信号処理関数

• conv：畳み込み演算（コンボリューション）

  2つのベクトル間の畳み込み演算を実行する．

• deconv：逆畳み込み演算
• conv2：2次元畳み込み演算

  2つの行列間の畳み込み演算を実行する．

• fft：高速フーリエ変換
• ifft：逆高速フーリエ変換
• fft2：2次元高速フーリエ変換
• ifft2：2次元逆高速フーリエ変換
• fftshift：フーリエ変換結果の並べ替え

  配列やベクトルの中央に周波数0の成分が来るように並び替えを行う．

フィルタリング関数

• filter：フィルタ処理の実行

  インパルス応答の計算例を以下に示す．

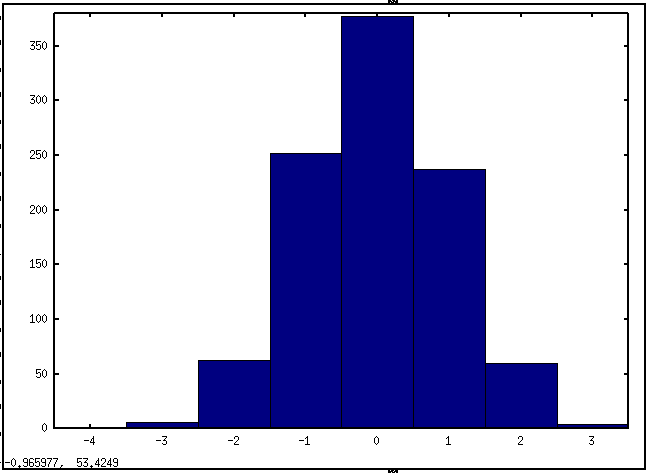
  plot( filter(1, [1 0.9], [1 zeros(1, 99)]') );
  

  
• fir1：単一帯域FIRフィルタの設計（窓関数法）

  ローパス，ハイパス，バンドパス，バンドストップフィルタの設計が可能である．

• fir2：複数帯域FIRフィルタの設計（窓関数法）
• firls：複数帯域FIRフィルタの設計（最小二乗法）
• remez：複数帯域FIRフィルタの設計（ミニマックス法）
• butter：バターワースフィルタの設計
• filtfilt：ゼロ位相フィルタ処理
• hamming：ハミング窓関数
• hanning：ハニング窓関数
• bartlett：バートレット窓関数
• blackman：ブラックマン窓関数
• kaiser：カイザー窓関数

補間関数

• interp1：1次元補間
• interp2：2次元補間

制御構造

• forループ
  
• whileループ
  
• if条件分岐
  

外部ライブラリとの連携

Forgeパッケージの利用

Octave Forgeは，Octaveの機能を拡張する公式パッケージリポジトリである．pkg関数を使用してパッケージを管理する．

pkg list                      % インストール済みパッケージの一覧表示
pkg install -forge control    % 制御系設計用パッケージのインストール
pkg load control             % パッケージのロード
pkg unload control           % パッケージのアンロード
pkg uninstall control        % パッケージのアンインストール

主要な公式パッケージのインストール例を以下に示す．

pkg install -forge signal     % 信号処理パッケージ
pkg install -forge image      % 画像処理パッケージ
pkg install -forge statistics % 統計解析パッケージ
pkg install -forge io        % 入出力機能拡張パッケージ
pkg install -forge optim     % 最適化パッケージ

Pythonとの連携

Python連携の初期設定を以下に示す．

% Pythonのパスを指定（環境に応じて変更）
setenv("PYTHON", "C:/Program Files/Python312/python.exe");
py_init;                      % Python環境の初期化

py_eval関数を使用してPythonコードを実行できる．

py_eval("import numpy as np");
py_eval("x = np.array([1, 2, 3])");
result = py_eval("x * 2");    % Python配列の演算

OctaveとPython間でデータを受け渡す例を以下に示す．

% OctaveからPythonへ
x = [1 2 3; 4 5 6];
py_eval("y = np.array(" + mat2str(x) + ")");

% PythonからOctaveへ
result = py_eval("y.tolist()");

C/C++との連携

Windows環境では，MinGW-w64コンパイラを使用してMEXファイルをビルドする．

% MEXファイルのコンパイル
mkoctfile --mex example.cpp

% MEXファイルの使用
result = example(input_data);

動的ライブラリ（DLL）を使用する例を以下に示す．

loadlibrary('example.dll', 'example.h');
result = calllib('example', 'function_name', args);
unloadlibrary('example');

Windowsシステムコマンドとの連携

system関数を使用してWindowsコマンドを実行できる．

[status, output] = system('dir');      % Windowsコマンドの実行
status = system('explorer .');         % エクスプローラーを開く

環境変数の操作例を以下に示す．

getenv('PATH');                        % 環境変数の取得
setenv('CUSTOM_VAR', 'value');         % 環境変数の設定

連携時の注意点

外部ライブラリとの連携時は，以下の点に注意する必要がある．

メモリ管理： 大規模なデータを扱う場合は，メモリリークを防ぐために適切なクリーンアップ処理を実装する．

エラー処理： 外部連携時のエラーは，try-catch構文で適切に処理する必要がある．特にPython連携時は，Pythonの例外をOctave側で捕捉する．

パス設定の確認： 外部ライブラリやPythonとの連携時は，システムのPATH設定が正しく行われていることを確認する．不適切なPATH設定は，予期しないエラーの原因となる．

ファイルの入出力

CSVファイルの操作

csvread関数を使用してCSVファイルを読み込む．

data = csvread('input.csv');           % 基本的な読み込み
data = csvread('input.csv', 1, 0);     % 2行目から読み込み（ヘッダーをスキップ）
data = csvread('input.csv', 0, 0, [0 0 2 3]); % 特定範囲の読み込み

csvwrite関数を使用してCSVファイルを書き込む．

A = [1 2 3; 4 5 6; 7 8 9];
csvwrite('output.csv', A);             % 基本的な書き込み
csvwrite('output.csv', A, 1, 0);       % 2行目から書き込み

dlmread関数とdlmwrite関数を使用すると，区切り文字を指定できる．

data = dlmread('input.txt', '\t');     % タブ区切りファイルの読み込み
dlmwrite('output.txt', A, '\t');       % タブ区切りファイルの書き込み

テキストファイルの操作

textread関数を使用してテキストファイルを読み込む．

[names, ages] = textread('data.txt', '%s %d');     % 文字列と数値の読み込み

低レベルのファイル操作を行う例を以下に示す．

fid = fopen('input.txt', 'r');                     % ファイルを開く
line = fgetl(fid);                                 % 1行読み込み
fclose(fid);                                       % ファイルを閉じる

fprintf関数を使用してテキストファイルを書き込む．

fid = fopen('output.txt', 'w');                    % 書き込みモードでファイルを開く
fprintf(fid, 'x = %f, y = %f\n', x, y);           % フォーマット指定して書き込み
fclose(fid);                                       % ファイルを閉じる

Excelファイルの操作

pkg install -forge io
pkg load io

[num, txt, raw] = xlsread('data.xlsx');           % 数値，テキスト，全データの読み込み
data = xlsread('data.xlsx', 'Sheet1');            % 特定シートの読み込み
data = xlsread('data.xlsx', 'A1:D10');            % 特定範囲の読み込み

xlswrite('output.xlsx', A);                       % 基本的な書き込み
xlswrite('output.xlsx', A, 'Sheet1');             % 特定シートへの書き込み
xlswrite('output.xlsx', A, 'Sheet1', 'B2');       % 特定位置への書き込み

fid = fopen('data.bin', 'rb');                    % バイナリ読み込みモード
data = fread(fid, [100 1], 'double');             % 倍精度実数として読み込み
fclose(fid);

fid = fopen('output.bin', 'wb');                  % バイナリ書き込みモード
fwrite(fid, A, 'double');                         % 倍精度実数として書き込み
fclose(fid);

save('workspace.mat');                            % 全変数を保存
save('data.mat', 'x', 'y');                      % 特定変数のみ保存
load('workspace.mat');                            % データの読み込み

dir('*.csv');                                     % ファイル一覧の取得
exist('file.txt', 'file');                        % ファイルの存在確認
mkdir('newdir');                                  % ディレクトリの作成
cd('path/to/directory');                          % ディレクトリの移動

[pathstr, name, ext] = fileparts('path/to/file.txt');  % パスの分解
fullfile('path', 'to', 'file.txt');                    % パスの結合

try
    x = 1/0;
catch err
    disp(['エラーメッセージ: ' err.message]);
    disp(['エラー識別子: ' err.identifier]);
end

function result = divide(a, b)
    if b == 0
        error('DIVIDE:ZeroDivisor', '0による除算は許可されていない．');
    end
    result = a/b;
end

warning('off', 'all');           % 全ての警告を無効化
warning('on', 'all');            % 全ての警告を有効化
warning('query', 'all');         % 警告の状態を確認

dbstop in function_name        % 関数内にブレークポイントを設定
dbstop if error               % エラー発生時に停止
dbstep                        % 1行実行
dbcont                        % 実行継続
dbquit                        % デバッグモード終了

whos                          % メモリ内の全変数の情報を表示
who                           % メモリ内の変数名一覧を表示
isnumeric(x)                  % 数値型かどうかを確認
ischar(x)                     % 文字型かどうかを確認
isempty(x)                    % 空かどうかを確認

tic;                          % 時間計測開始
A = rand(1000);              % 計測対象の処理
B = A * A;
elapsed_time = toc;          % 計測終了，経過時間を取得

profile on                    % プロファイリング開始
% 計測対象の処理を実行
profile off                   % プロファイリング終了
profile report               % 結果レポートを表示

verbosity(0);                 % 最小限の出力
verbosity(1);                 % 通常の出力
verbosity(2);                 % 詳細な出力

disp('デバッグメッセージ');
printf('変数xの値: %f\n', x);

pause;                        % キー入力まで待機
pause(2);                     % 2秒間待機