社会ネットワーク分析（SNA: Social Network Analysis）

社会ネットワーク分析（SNA）は、グラフ理論を基盤として個体間の関係を定量的に分析する手法である。従来の統計手法が個体の属性に着目するのに対し、SNAは「誰と誰が、どのようにつながっているか」を分析対象とする。

SNAではネットワークをノード（アクター）とエッジ（関係）で表現する。有向グラフを用いることで、引用関係や影響関係のような方向性のある関係を扱える。エッジに重みを付与すれば、関係の強さや頻度も考慮できる。

主要な分析指標として、ネットワーク全体の結合度を示す密度、ノードの重要性を評価する中心性指標（入次数・出次数中心性、媒介中心性、近接中心性、PageRank）がある。これらの指標を組み合わせることで、ネットワーク内の各アクターの役割や位置づけを多角的に評価できる。

本記事では、論文の引用ネットワークを例として、PythonのNetworkXライブラリを用いた実装と各指標の計算結果の解釈を示した。

スライド資料: [PDF], [パワーポイント]

YouTube動画：https://youtu.be/M9GsYdYJ1pU

1. 概要

社会ネットワーク分析（SNA: Social Network Analysis）は、グラフ理論を用いて社会構造を分析する手法である。SNAではネットワークをノード（node）とエッジ（edge）で表現する。ノードは人物、組織などを表し、エッジはノード間の関係を表す。エッジには重み（weight）を付与できる。

2. 他の分析手法との比較

SNAは個体間の関係を分析対象とする。従来の統計手法は個体の属性（年齢、性別、収入など）に着目し、サンプルの独立性を仮定する（補足：相関分析など関係性を扱う統計手法も存在する）。SNAは誰と誰がつながっているか、どのようにつながっているかを定量化する。

3. 原理

3.1 基本構造：グラフ表現

ネットワークはグラフ G = (V, E) で表現する。Vはノードの集合、Eはエッジの集合である。

グラフには無向グラフと有向グラフがある。無向グラフはエッジに方向性がなく、友人関係のような双方向の関係を表す。有向グラフはエッジに方向性があり、引用関係や影響関係を表す。本記事では有向グラフを扱う。

エッジには重みを付与できる。重みは関係の強さや頻度を表す。例えば、引用回数や影響の強さを重みとして設定する。

3.2 主要な分析指標

以下の指標でネットワーク構造を評価する。指標によって重みの扱いが異なる。媒介中心性、近接中心性、PageRankは重みを考慮し、密度と次数中心性は考慮しない。

ネットワーク全体の指標

「密度（Density）」は、実際のエッジ数を最大エッジ数で割った値である。有向グラフでは、A→BとB→Aは別のエッジとして数える。最大エッジ数はN × (N-1)、密度は D = E / (N × (N-1)) である（Nはノード数、Eはエッジ数）。密度は重みを考慮しない。

ノードレベルの指標（中心性指標）

「次数中心性（Degree Centrality）」は、ノードに接続するエッジの数である。有向グラフでは入次数と出次数を区別する。次数中心性は重みを考慮しない。

「入次数中心性（In-degree Centrality）」は、そのノードに入るエッジの数である。被参照数やフォロワー数に相当し、受信者としての重要性を示す。

「出次数中心性（Out-degree Centrality）」は、そのノードから出るエッジの数である。参照数やフォロー数に相当し、発信者としての活発さを示す。

「媒介中心性（Betweenness Centrality）」は、他のノード間の最短経路上にそのノードが含まれる頻度である。仲介者としての重要性を示す。重み付きエッジの場合、重みの逆数を距離として計算する。重みが大きいほど距離が近いと解釈する。

「近接中心性（Closeness Centrality）」は、他の全ノードからそのノードへの平均経路長の逆数である。他のノードからの到達しやすさを示す。入ってくるエッジがないノードは値が0になる。重み付きエッジの場合、重みの逆数を距離として計算する。重みが大きいほど距離が近いと解釈する。近接中心性には出方向と入方向の2種類がある。出方向は引用先への到達しやすさ（参照の効率性）を示し、入方向は引用元からの到達しやすさ（被引用の容易さ）を示す。本記事では入方向の近接中心性を扱う。

「PageRank」は、重要なノードからリンクされているノードほど値が高い。入次数だけでなくリンク元の重要性も考慮する。重み付きエッジの場合、重みに応じてスコア配分が変わる。

3.3 重みがない場合

エッジに重みを設定しない場合、すべてのエッジの重みを1として扱う。この場合、媒介中心性と近接中心性はホップ数で経路長を計算する。PageRankはすべてのエッジを同等に扱う。

重みがない場合は関係の有無のみを分析する。関係の強さを考慮しない場合や、重みのデータがない場合に用いる。

4. サンプルによる説明

4.1 サンプルネットワーク

論文の引用ネットワークを例とする。論文Aが論文Bを引用する場合、A→Bのエッジを作成する。重みは引用の重要度を表す。値が大きいほど重要な引用である。

サンプルネットワーク（引用関係）:
    A → B → D
    ↓ ↘ ↓
    C → E ← F

エッジと重み:
A → B (重み: 3)
A → C (重み: 1)
A → E (重み: 2)
B → D (重み: 2)
B → E (重み: 1)
C → E (重み: 3)
F → E (重み: 2)

4.2 Pythonによる実装

以下にNetworkXライブラリを用いた実装を示す。

import networkx as nx
import matplotlib.pyplot as plt

# 有向グラフの構築（重み付き）
G = nx.DiGraph()
edges = [
    ('A', 'B', 3), ('A', 'C', 1), ('A', 'E', 2),
    ('B', 'D', 2), ('B', 'E', 1),
    ('C', 'E', 3),
    ('F', 'E', 2)
]
G.add_weighted_edges_from(edges)

# 重みの逆数を距離として設定
for u, v, data in G.edges(data=True):
    data['distance'] = 1 / data['weight']

# 入次数中心性と出次数中心性（重みは考慮されない）
in_degree_cent = nx.in_degree_centrality(G)
out_degree_cent = nx.out_degree_centrality(G)

# 媒介中心性（重みの逆数を距離として使用）
betweenness_cent = nx.betweenness_centrality(G, weight='distance')

# 近接中心性（重みの逆数を距離として使用）
closeness_cent = nx.closeness_centrality(G, distance='distance')

# PageRank（重みを考慮）
pagerank = nx.pagerank(G, weight='weight')

# 結果の表示
print("=== 入次数中心性 ===")
for node, cent in sorted(in_degree_cent.items()):
    print(f"  {node}: {cent:.3f}")

print("\n=== 出次数中心性 ===")
for node, cent in sorted(out_degree_cent.items()):
    print(f"  {node}: {cent:.3f}")

print("\n=== 媒介中心性（重み付き） ===")
for node, cent in sorted(betweenness_cent.items()):
    print(f"  {node}: {cent:.3f}")

print("\n=== 近接中心性（重み付き） ===")
for node, cent in sorted(closeness_cent.items()):
    print(f"  {node}: {cent:.3f}")

print("\n=== PageRank（重み付き） ===")
for node, cent in sorted(pagerank.items()):
    print(f"  {node}: {cent:.3f}")

# ネットワーク全体の指標
print(f"\n=== ネットワーク全体の指標 ===")
print(f"  ノード数: {G.number_of_nodes()}")
print(f"  エッジ数: {G.number_of_edges()}")
print(f"  密度: {nx.density(G):.3f}")

# ネットワークの可視化
pos = nx.spring_layout(G, seed=42)
edge_labels = nx.get_edge_attributes(G, 'weight')
nx.draw(G, pos, with_labels=True, node_color='lightgreen', node_size=700, font_size=14, arrows=True)
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
plt.show()

4.3 実行結果

=== 入次数中心性 ===
  A: 0.000
  B: 0.200
  C: 0.200
  D: 0.200
  E: 0.800
  F: 0.000

=== 出次数中心性 ===
  A: 0.600
  B: 0.400
  C: 0.200
  D: 0.000
  E: 0.000
  F: 0.200

=== 媒介中心性（重み付き） ===
  A: 0.000
  B: 0.050
  C: 0.000
  D: 0.000
  E: 0.000
  F: 0.000

=== 近接中心性（重み付き） ===
  A: 0.000
  B: 0.600
  C: 0.200
  D: 0.600
  E: 1.371
  F: 0.000

=== PageRank（重み付き） ===
  A: 0.101
  B: 0.144
  C: 0.116
  D: 0.183
  E: 0.355
  F: 0.101

=== ネットワーク全体の指標 ===
  ノード数: 6
  エッジ数: 7
  密度: 0.233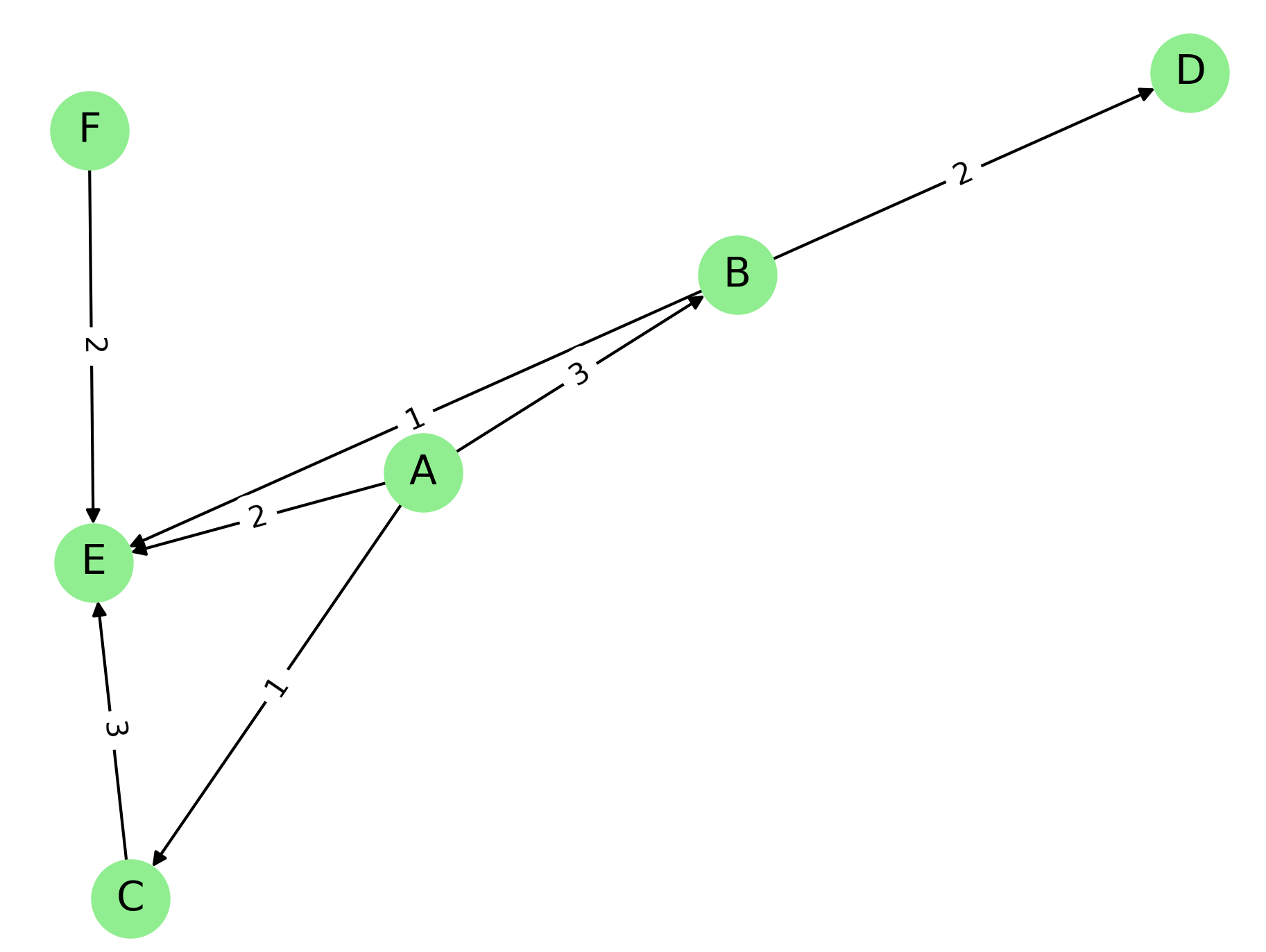

4.4 結果の解釈

入次数中心性と出次数中心性: Eの入次数中心性が0.800と最も高い。4つの論文から引用されている。AとFは0.000で、引用されていない。出次数中心性はAが0.600と最も高い。3つの論文を引用している。DとEは0.000で、引用していない。

媒介中心性: Bのみが0.050を示す（A→D経路の仲介）。他のノードは0.000である。

近接中心性: Eが1.371と最も高い。4つのノードから引用され、到達されやすい。BとDが0.600である。それぞれ引用元から短い距離にある。AとFは0.000である。引用されておらず、他から到達できない。

PageRank: Eが0.355と最も高い。4つのノードからリンクされている。Dが0.183である。Bからのみリンクされるが、Bの重要度が反映されている。

密度: 密度0.233は、最大30本（6×5）のうち7本のエッジが存在することを示す。

5. まとめ

SNAは個体間の関係を分析する手法である。中心性指標などを用いて、ネットワーク内のアクターの位置づけや全体構造を評価する。方向性のある関係には有向グラフを用い、入次数・出次数中心性やPageRankで分析する。エッジに重みを設定すると、関係の強さを考慮した分析ができる。