シミュレーションと3次元コンピュータグラフィックス
【概要】Panda3Dを用いた3種類の物理シミュレーションプログラムを解説する。重力N体シミュレーションによる銀河衝突、Boidsアルゴリズムによる群れ行動、格子法による流体シミュレーション(煙の拡散と上昇気流)を実装し、物理法則に基づく自然現象の可視化手法を学ぶ。
【目次】
【サイト内の関連ページ】
- Panda3D 3次元ゲームエンジン入門: 別ページ »で説明
- Panda3Dゲームエンジン中級編:システム構築の基礎 別ページ »で説明
- WindowsでのPanda3Dのインストール: 別ページ »で説明
- UbuntuでのPanda3Dのインストール: 別ページ »で説明
- Panda3Dの機能概要(説明資料)[PDF]、[パワーポイント]
重力N体シミュレーション(銀河衝突)
予備知識
万有引力の法則
ニュートンの万有引力の法則は、質量を持つ2つの物体が互いに引き合う力を記述する。力の大きさは両者の質量の積に比例し、距離の2乗に反比例する。F = G × m1 × m2 / r²で表される。Gは万有引力定数、m1とm2は質量、rは距離である。この法則から、惑星の軌道や銀河の運動といった天体現象を説明できる。
N体問題と数値計算
多数の天体が相互に重力を及ぼし合う系をN体問題と呼ぶ。各天体について全ての他天体との間に働く重力を計算し、ニュートンの運動方程式F = maに基づいて位置と速度を時間発展させる。N個の天体では、全ペアの組み合わせN × (N - 1) / 2通りの重力計算が必要であり、計算量はO(N²)となる。時間発展には数値積分法を用いる。本プログラムではオイラー法を採用する。
実装例
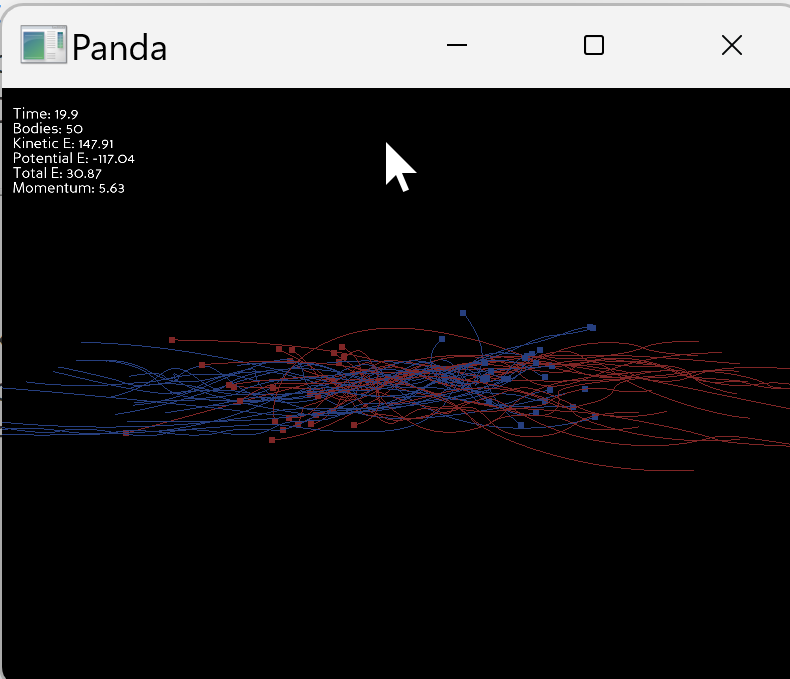
Panda3Dで2つの銀河の衝突をシミュレーションするプログラムである。各銀河は25個の天体で構成され、合計50個の天体が相互作用する。天体は点で表示され、過去の軌跡は線で描画される。物理量(エネルギー、運動量)を画面に表示し、シミュレーションの正確性を確認できる。
Bodyクラス(天体の表現)
各天体をBodyクラスで表現する。天体は位置(x, y, z)、速度(vx, vy, vz)、質量、表示色の情報を持つ。軌跡は過去500ステップ分の位置を記録し、古い点から順に削除される。
位置の記録にはリストのスライス記法(pos[:])でコピーを作成する。self.trail.append(self.pos)と書くと、リストにposの参照が追加される。posは常に同じオブジェクトを指すため、全ての軌跡点が現在位置を指してしまう。pos[:]はposの内容をコピーした新しいリストを作成するため、その時点の位置が正しく記録される。
物理パラメータ
シミュレーションを制御するパラメータを以下に示す。
- 万有引力定数(G):1.0。実際の物理定数(6.67 × 10⁻¹¹)とは異なるスケール調整済みの値であり、見やすい運動速度を実現する
- ソフトニングパラメータ(softening):0.5。天体が接近したときの重力の発散を防ぐ
- 時間刻み幅(dt):0.01。位置と速度の更新間隔
ソフトニングパラメータの役割
2つの天体が近づくと、距離rが0に近づき重力F = G × m1 × m2 / r²が無限大に発散する。これは数値計算の破綻を引き起こす。ソフトニングパラメータεを導入し、r² + ε²を距離の2乗として用いることで発散を防ぐ。
r_squared = dx² + dy² + dz² + ε²、r = √r_squaredと計算する。r >> εのとき、ε²の影響は無視できrとほぼ等しい。r ≈ εのとき、距離が実際より大きく見積もられ、重力が弱められる。物理的には不正確だが、数値安定性を確保するための実用的手法である。
銀河の生成
2つの銀河を生成する。銀河1は左側(x = -30)に配置され、右向き(vx = 2.0)に移動する。銀河2は右側(x = 30)に配置され、左向き(vx = -2.0)に移動する。各銀河内の天体は円盤状に配置される。
天体の位置は極座標(r, θ)でランダムに決定し、直交座標(x, y)に変換する。中心からの距離rは2~15の範囲、角度θは0~2πの範囲からランダムに選ぶ。高さ方向(z座標)は-2~2の範囲からランダムに選び、銀河に厚みを持たせる。極座標から直交座標への変換式は、x = 銀河中心x + r × cos(θ)、y = 銀河中心y + r × sin(θ)である。
各天体には銀河中心周りの回転速度を与える。中心に質量が集中していると仮定すると、万有引力と遠心力の釣り合いから円軌道の速度はv ∝ √(1/r)となる。orbital_speed = 1.5 × √(1.0 / max(r, 1.0))で計算する。係数1.5は見やすい回転速度を実現するための調整値である。max(r, 1.0)はr < 1のときの発散を防ぐ。
速度ベクトルは銀河全体の移動速度と回転速度を合成する。x方向速度vx = 銀河移動速度x - orbital_speed × sin(θ)、y方向速度vy = 銀河移動速度y + orbital_speed × cos(θ)となる。sin(θ)とcos(θ)の符号により、天体が中心周りに反時計回りに回転する。円運動の接線方向の速度成分は、(-sin(θ), cos(θ))で表される。z方向速度vzは-0.2~0.2の範囲からランダムに選び、3次元的な動きを与える。
重力の計算
全天体間の重力を計算する関数calculate_forces()を実装する。天体数N = 50のとき、全ペアの組み合わせは50 × 49 / 2 = 1225通りである。
二重ループfor i in range(N)、for j in range(i + 1, N)により、各ペアを1回だけ計算する。j = i + 1から開始することで、(i, j)のペアと(j, i)のペアの重複を避ける。
天体iと天体jの相対位置ベクトル(dx, dy, dz)を計算する。dx = 天体jのx座標 - 天体iのx座標、dy、dzも同様である。距離の2乗r² = dx² + dy² + dz² + ε²を計算する。ε²はソフトニングパラメータの2乗である。距離r = √r²を求める。
万有引力の大きさF = G × mi × mj / r²を計算する。力のベクトル成分は、力の大きさ × 単位ベクトルで求める。単位ベクトルは相対位置ベクトルを距離で割ったものである。x方向の力fx = F × dx / r、y方向の力fy = F × dy / r、z方向の力fz = F × dz / rとなる。
作用反作用の法則により、天体iには天体jに向かう力(fx, fy, fz)が働き、天体jには天体iに向かう逆向きの力(-fx, -fy, -fz)が働く。forces[i]に(fx, fy, fz)を加算し、forces[j]から(fx, fy, fz)を減算する。この方法により、天体iと天体jの間の重力は1回だけ計算すれば十分であり、計算量を半減できる。
時間積分
ニュートンの運動方程式F = maから加速度a = F / mを計算する。各天体について、ax = Fx / m、ay = Fy / m、az = Fz / mを求める。
速度をv = v + a × dtで更新し、位置をx = x + v × dtで更新する。これをオイラー法と呼ぶ。本プログラムは教育目的であり、オイラー法の単純さと理解しやすさを優先する。dt = 0.01により短時間シミュレーションでは実用的な精度が得られる。
軌跡は5フレームごとに記録する。毎フレーム記録すると軌跡点が多すぎて描画負荷が高くなる。5フレームに1回の記録で軌跡の滑らかさと計算効率のバランスをとる。add_trail_point()メソッドで現在位置を軌跡リストに追加し、リスト長が500を超えたら最古の点を削除する。
エネルギーと運動量の計算
物理シミュレーションの正確性を検証するため、全エネルギーと全運動量を計算する。
運動エネルギーK = (1/2) × m × v²を全天体について合計する。v²は速度ベクトルの大きさの2乗vx² + vy² + vz²である。
位置エネルギーU = -G × m1 × m2 / rを全ペアについて合計する。符号が負になるのは、重力が引力であり無限遠を基準とするためである。天体が近づくと位置エネルギーは減少(より負に)し、運動エネルギーが増加する。
全エネルギーE = K + Uは保存量であり、理想的には一定値を保つ。数値誤差により微小変動するが、大きく変化する場合は時間刻み幅が不適切である。本プログラムではdt = 0.01と設定し、エネルギー保存を確認できる。
運動量p = m × vを全天体について合計する。外力が働かない孤立系では運動量ベクトルは保存される。本シミュレーションでは外力がなく、初期設定で銀河1が右向き、銀河2が左向きに移動するため、全運動量の大きさは0に近い値となる。この値がシミュレーション中も変化しないことで、運動量保存を確認できる。
天体メッシュの更新
各天体の位置を点で描画する。GeomVertexDataに各天体の座標を書き込む。GeomVertexWriterを用いて、setData3(x, y, z)で座標を更新する。天体の色は生成時に設定した色(青または赤)を保持する。
点のサイズはsetRenderMode(RenderModeAttrib.MPoint, 6.0)で6ピクセルに設定する。背景色は黒のため、青と赤の点が明瞭に見える。
軌跡の描画
各天体の過去の軌跡を線分の集合で描画する。軌跡がN点あるとき、線分は(N - 1)本である。例えば、軌跡が500点なら線分は499本となる。各線分は始点と終点の2頂点が必要なため、総頂点数は(N - 1) × 2 = 998頂点となる。
軌跡の長さは天体ごとに異なる。シミュレーション開始直後は軌跡が0点、時間経過とともに増加し、最大500点に達する。必要な頂点数を毎フレーム計算し、GeomVertexDataのサイズを動的に設定する。
total_vertices = 0で初期化し、各天体の軌跡について(len(trail) - 1) × 2を累積する。setNumRows(total_vertices)により、頂点データの行数を変更する。
各線分について、始点と終点の座標と色を設定する。GeomVertexWriterでvertex.setData3(x, y, z)により座標を、color.setData4(r, g, b, a)により色を書き込む。色の不透明度(アルファ値a)は軌跡の古さに応じて変化させる。
alpha = (i + 1) / len(trail) × 0.7により計算する。iは軌跡リスト内のインデックスであり、i = 0が最古、i = len(trail) - 1が最新である。最古の点では(0 + 1) / 500 × 0.7 ≈ 0.001、最新の点では(499 + 1) / 500 × 0.7 = 0.7となる。古い軌跡ほど薄く表示され、フェードアウト効果が得られる。
GeomLinesプリミティブに頂点インデックスのペアを追加する。lines.addVertices(vertex_index, vertex_index + 1)により、連続する2頂点を線分として登録する。vertex_indexは0から始まり、2ずつ増加する。
clearPrimitives()で前フレームの線分を削除し、新しい線分を追加する。これにより軌跡が動的に更新される。
物理量の表示
画面左上にOnscreenTextで物理量を表示する。表示内容は時間、天体数、運動エネルギー、位置エネルギー、全エネルギー、運動量である。
calculate_energy()で運動エネルギーkinetic、位置エネルギーpotential、全エネルギーtotal = kinetic + potentialを計算する。calculate_momentum()で運動量の3成分(px, py, pz)を計算し、大きさp_magnitude = √(px² + py² + pz²)を求める。
これらの値をフォーマットした文字列をsetText()で表示する。全エネルギーと運動量がほぼ一定であることを確認することで、シミュレーションの正確性を検証できる。
メインループ
updateタスクが毎フレーム呼び出される。1フレームあたり物理計算を5回実行する。描画フレームレートは約60FPS(1フレーム ≈ 0.016秒)だが、物理時間刻み幅はdt = 0.01秒である。5回実行することで5 × 0.01 = 0.05秒の物理時間を進め、描画と物理時間の進行を同期させる。
5回の物理計算の後、update_mesh()で天体の位置を更新し、update_trails()で軌跡を更新し、update_info_text()で物理量表示を更新する。
カメラ設定
カメラを位置(0, -100, 40)に配置し、原点(0, 0, 0)を注視する。銀河の衝突を斜め上から見下ろす視点となる。背景色は黒(0, 0, 0)に設定し、天体と軌跡を見やすくする。Panda3Dのデフォルトマウス操作(左クリックドラッグで回転、右クリックドラッグでズーム、中クリックドラッグで平行移動)が使用可能である。
実行結果
プログラムを実行すると、2つの銀河が左右から接近し衝突する。衝突前は各銀河内で天体が規則的に回転する。青色の銀河(左側)は右向きに移動し、赤色の銀河(右側)は左向きに移動する。各天体は銀河中心周りを回転しながら全体として移動する。
衝突時には銀河形状が大きく変形し、天体の軌道が複雑に変化する。2つの銀河が重なり合うと、相互の重力により天体が加速または減速される。一部の天体は高速で散乱され、銀河から放出される。これは重力による散乱現象であり、3体以上の相互作用により発生する。
衝突後は2つの銀河が融合し、不規則な形状を形成する。初期の規則的な円盤構造は失われ、天体が広範囲に分布する。一部の天体は互いに束縛され楕円軌道を描き、一部は十分な速度を得て系から脱出する。
軌跡表示により、各天体の運動経路が可視化される。衝突前は滑らかな円軌道、衝突時は複雑に曲がった軌道、衝突後は直線的または楕円的な軌道が観察できる。軌跡の色(青または赤)により、どちらの銀河に属していたかを識別できる。
画面左上に表示される物理量から、シミュレーションの正確性を確認できる。全エネルギー(Total E)は初期値からわずかに変動するが、大きくは変化しない。運動量(Momentum)は初期値0付近を保つ。これらの保存則がほぼ成立することで、数値計算が妥当であることを検証できる。エネルギーの微小変動はオイラー法の数値誤差によるものであり、長時間シミュレーションでは誤差が蓄積する。
演習
手順
- プログラムを実行し、2つの銀河(青25個、赤25個)が衝突する様子を観察する
- 画面左上に表示される物理量(運動エネルギー、位置エネルギー、全エネルギー、運動量)の変化を記録する
- 全エネルギーと運動量がほぼ一定に保たれることを確認する
from direct.showbase.ShowBase import ShowBase
from direct.task import Task
from panda3d.core import GeomVertexFormat, GeomVertexData, GeomVertexWriter
from panda3d.core import Mat4, PointLight, AmbientLight, VBase4
from panda3d.core import Geom, GeomNode, GeomPoints, GeomLines
from panda3d.core import RenderModeAttrib
from panda3d.core import TextNode
from direct.gui.OnscreenText import OnscreenText
import numpy as np
import random
import math
class Body:
"""天体を表すクラス"""
def __init__(self, x, y, z, vx, vy, vz, mass, color):
self.pos = np.array([x, y, z], dtype=np.float64)
self.vel = np.array([vx, vy, vz], dtype=np.float64)
self.mass = mass
self.color = color
self.trail = [] # 軌跡を記録
self.max_trail_length = 500 # 軌跡の最大長
def add_trail_point(self):
"""現在位置を軌跡に追加"""
self.trail.append(self.pos.copy())
if len(self.trail) > self.max_trail_length:
self.trail.pop(0)
class GalaxyCollision(ShowBase):
def __init__(self):
ShowBase.__init__(self)
# 背景色を黒に設定
self.setBackgroundColor(0, 0, 0)
# 物理定数
self.G = 1.0 # 万有引力定数(スケール調整済み)
self.softening = 0.5 # ソフトニングパラメータ(衝突時の発散防止)
self.dt = 0.01 # 時間刻み幅
# 天体リスト
self.bodies = []
# 銀河を生成
self.create_galaxies()
# パーティクルメッシュの作成
self.particle_mesh = self.create_particle_mesh()
self.particle_node = self.render.attachNewNode(self.particle_mesh)
self.particle_node.setTextureOff(1)
self.particle_node.setRenderMode(RenderModeAttrib.MPoint, 6.0) # ポイントサイズ6
# 軌跡メッシュの作成
self.trail_mesh = self.create_trail_mesh()
self.trail_node = self.render.attachNewNode(self.trail_mesh)
self.trail_node.setTextureOff(1)
# ライティング設定
alight = AmbientLight('alight')
alight.setColor(VBase4(0.5, 0.5, 0.5, 1))
alnp = self.render.attachNewNode(alight)
self.render.setLight(alnp)
# カメラ設定
self.disableMouse()
self.camera.setPos(0, -100, 40)
self.camera.lookAt(0, 0, 0)
mat = Mat4(self.camera.getMat())
mat.invertInPlace()
self.mouseInterfaceNode.setMat(mat)
self.enableMouse()
# 物理量表示用テキスト
self.info_text = OnscreenText(
text='',
pos=(-1.3, 0.9),
scale=0.05,
fg=(1, 1, 1, 1),
align=TextNode.ALeft
)
# シミュレーション時間
self.sim_time = 0.0
self.frame_count = 0
self.taskMgr.add(self.update, "updateTask")
self.prev_time = globalClock.getFrameTime()
def create_galaxies(self):
"""2つの銀河を生成"""
num_stars_per_galaxy = 25 # 各銀河の天体数
# 銀河1(左側、青色)
galaxy1_center = np.array([-30.0, 0.0, 0.0])
galaxy1_velocity = np.array([2.0, 0.0, 0.0]) # 右向きに移動
for _ in range(num_stars_per_galaxy):
# 銀河中心からの距離と角度(円盤状に配置)
r = random.uniform(2, 15)
theta = random.uniform(0, 2 * math.pi)
z = random.uniform(-2, 2)
# 位置
x = galaxy1_center[0] + r * math.cos(theta)
y = galaxy1_center[1] + r * math.sin(theta)
z = galaxy1_center[2] + z
# 銀河回転速度(円運動)
orbital_speed = 1.5 * math.sqrt(1.0 / max(r, 1.0))
vx = galaxy1_velocity[0] - orbital_speed * math.sin(theta)
vy = galaxy1_velocity[1] + orbital_speed * math.cos(theta)
vz = random.uniform(-0.2, 0.2)
mass = random.uniform(0.5, 1.5)
color = (0.3, 0.5, 1.0, 1.0) # 青色
self.bodies.append(Body(x, y, z, vx, vy, vz, mass, color))
# 銀河2(右側、赤色)
galaxy2_center = np.array([30.0, 0.0, 0.0])
galaxy2_velocity = np.array([-2.0, 0.0, 0.0]) # 左向きに移動
for _ in range(num_stars_per_galaxy):
r = random.uniform(2, 15)
theta = random.uniform(0, 2 * math.pi)
z = random.uniform(-2, 2)
x = galaxy2_center[0] + r * math.cos(theta)
y = galaxy2_center[1] + r * math.sin(theta)
z = galaxy2_center[2] + z
orbital_speed = 1.5 * math.sqrt(1.0 / max(r, 1.0))
vx = galaxy2_velocity[0] - orbital_speed * math.sin(theta)
vy = galaxy2_velocity[1] + orbital_speed * math.cos(theta)
vz = random.uniform(-0.2, 0.2)
mass = random.uniform(0.5, 1.5)
color = (1.0, 0.3, 0.3, 1.0) # 赤色
self.bodies.append(Body(x, y, z, vx, vy, vz, mass, color))
def create_particle_mesh(self):
"""天体可視化用のメッシュ作成"""
format = GeomVertexFormat.getV3c4()
vdata = GeomVertexData('bodies', format, Geom.UHDynamic)
vertex = GeomVertexWriter(vdata, 'vertex')
color = GeomVertexWriter(vdata, 'color')
for body in self.bodies:
vertex.addData3(*body.pos)
color.addData4(*body.color)
points = GeomPoints(Geom.UHDynamic)
points.addNextVertices(len(self.bodies))
geom = Geom(vdata)
geom.addPrimitive(points)
node = GeomNode('bodies_node')
node.addGeom(geom)
return node
def create_trail_mesh(self):
"""軌跡可視化用のメッシュ作成"""
format = GeomVertexFormat.getV3c4()
vdata = GeomVertexData('trails', format, Geom.UHDynamic)
# 初期状態では空
vdata.setNumRows(0)
geom = Geom(vdata)
node = GeomNode('trails_node')
node.addGeom(geom)
return node
def calculate_forces(self):
"""全天体間の重力を計算(NumPy版)"""
n = len(self.bodies)
forces = np.zeros((n, 3), dtype=np.float64)
# 位置と質量を配列に展開
positions = np.array([b.pos for b in self.bodies])
masses = np.array([b.mass for b in self.bodies])
for i in range(n):
for j in range(i + 1, n):
# 相対位置ベクトル
diff = positions[j] - positions[i]
# 距離の2乗(ソフトニングパラメータを追加)
r_squared = np.dot(diff, diff) + self.softening * self.softening
r = np.sqrt(r_squared)
# 万有引力の大きさ F = G * m1 * m2 / r²
force_magnitude = self.G * masses[i] * masses[j] / r_squared
# 力のベクトル
force = force_magnitude * diff / r
# 作用反作用の法則
forces[i] += force
forces[j] -= force
return forces
def update_physics(self):
"""速度ベルレ法による時間積分"""
# 現在の力を計算
forces = self.calculate_forces()
masses = np.array([b.mass for b in self.bodies])
# 速度と位置の更新
for i, body in enumerate(self.bodies):
# 加速度 a = F / m
acc = forces[i] / body.mass
# 速度の更新 v = v + a * dt
body.vel += acc * self.dt
# 位置の更新 x = x + v * dt
body.pos += body.vel * self.dt
# 軌跡に追加(5フレームごと)
if self.frame_count % 5 == 0:
body.add_trail_point()
def calculate_energy(self):
"""全エネルギーを計算(NumPy版)"""
positions = np.array([b.pos for b in self.bodies])
velocities = np.array([b.vel for b in self.bodies])
masses = np.array([b.mass for b in self.bodies])
# 運動エネルギー K = (1/2) * m * v²
v_squared = np.sum(velocities ** 2, axis=1)
kinetic = 0.5 * np.sum(masses * v_squared)
# 位置エネルギー U = -G * m1 * m2 / r
potential = 0.0
n = len(self.bodies)
for i in range(n):
for j in range(i + 1, n):
diff = positions[j] - positions[i]
r = np.sqrt(np.dot(diff, diff) + self.softening * self.softening)
potential -= self.G * masses[i] * masses[j] / r
return kinetic, potential, kinetic + potential
def calculate_momentum(self):
"""全運動量を計算(NumPy版)"""
velocities = np.array([b.vel for b in self.bodies])
masses = np.array([b.mass for b in self.bodies])
momentum = np.sum(masses[:, np.newaxis] * velocities, axis=0)
return momentum[0], momentum[1], momentum[2]
def update_mesh(self):
"""天体メッシュの更新"""
geom = self.particle_mesh.modifyGeom(0)
vdata = geom.modifyVertexData()
vertex = GeomVertexWriter(vdata, 'vertex')
for body in self.bodies:
vertex.setData3(*body.pos)
def update_trails(self):
"""軌跡メッシュの更新"""
geom = self.trail_mesh.modifyGeom(0)
vdata = geom.modifyVertexData()
# 必要な頂点数を計算
total_vertices = 0
for body in self.bodies:
if len(body.trail) >= 2:
total_vertices += (len(body.trail) - 1) * 2
# 頂点データのサイズを設定
vdata.setNumRows(total_vertices)
vertex = GeomVertexWriter(vdata, 'vertex')
color = GeomVertexWriter(vdata, 'color')
# 既存のラインプリミティブをクリア
geom.clearPrimitives()
lines = GeomLines(Geom.UHDynamic)
vertex_index = 0
for body in self.bodies:
if len(body.trail) < 2:
continue
# 軌跡の各セグメントを描画
for i in range(len(body.trail) - 1):
# 始点
vertex.setData3(*body.trail[i])
# アルファ値を軌跡の古さに応じて減衰
alpha = (i + 1) / len(body.trail) * 0.7
color.setData4(body.color[0], body.color[1], body.color[2], alpha)
# 終点
vertex.setData3(*body.trail[i + 1])
color.setData4(body.color[0], body.color[1], body.color[2], alpha)
# ラインを追加
lines.addVertices(vertex_index, vertex_index + 1)
vertex_index += 2
geom.addPrimitive(lines)
def update_info_text(self):
"""物理量表示の更新"""
kinetic, potential, total = self.calculate_energy()
px, py, pz = self.calculate_momentum()
p_magnitude = math.sqrt(px**2 + py**2 + pz**2)
text = f"Time: {self.sim_time:.1f}\n"
text += f"Bodies: {len(self.bodies)}\n"
text += f"Kinetic E: {kinetic:.2f}\n"
text += f"Potential E: {potential:.2f}\n"
text += f"Total E: {total:.2f}\n"
text += f"Momentum: {p_magnitude:.2f}"
self.info_text.setText(text)
def update(self, task):
current_time = globalClock.getFrameTime()
dt = current_time - self.prev_time
self.prev_time = current_time
if dt < 0.0001:
return Task.cont
# 物理演算を複数回実行(安定性向上)
for _ in range(5):
self.update_physics()
self.sim_time += self.dt
self.update_mesh()
self.update_trails()
self.update_info_text()
self.frame_count += 1
return Task.cont
app = GalaxyCollision()
app.run()
群れ行動シミュレーション(Boidsアルゴリズム)
鳥や魚の群れの動きを3つのルール(分離、整列、結合)で再現する。
概要
鳥や魚の群れは、リーダーなしで統一された集団行動を示す。このプログラムは、Craig Reynoldsが1987年に提案したBoidsアルゴリズムを3次元空間で実装する。各個体は周囲の仲間のみを認識して行動するが、そのルールから群れ全体の複雑な動きが生まれる。本プログラムはこの現象を可視化する。
プログラム構成
Boidクラス(個体の表現)
各個体をBoidクラスで表現する。個体は以下の情報を持つ。
状態変数
- 位置:3次元空間内の座標
- 速度:移動方向と速さ
- 加速度:速度の変化率
制約パラメータ
- 最大速度:8.0(移動速度の上限)
- 最大操舵力:0.4(1フレームあたりの速度変化の上限。急な方向転換を防ぎ滑らかな動きを実現する)
- 知覚半径:10.0(この距離以内の仲間を認識できる)
3つの行動ルール
各個体は知覚半径10.0以内の仲間のみを認識し、毎フレーム以下の3つのルールで進行方向を決定する。
ルール1:分離(衝突回避)
仲間に近づきすぎた場合、離れる方向に進む。反発力は距離の2乗に反比例する。例えば、距離が半分になると反発力は4倍になる。
ルール2:整列(速度の同期)
周囲の仲間の速度を平均し、自身の速度をその平均値に近づける。全体が同じ方向に移動する効果がある。
ルール3:結合(群れの維持)
周囲の仲間の位置を平均(重心を計算)し、その位置に向かって進む。群れの分散を防ぐ効果がある。
力の合成
3つのルールから得られる力を以下の重みで合成する。
- 分離:1.8(衝突回避を優先)
- 整列:1.5(速度の同期)
- 結合:1.8(群れの維持)
分離と結合の重みが同値で最も高いのは、衝突回避と群れの維持を同程度に重視するためである。合成後の力が最大操舵力0.4を超える場合、0.4に制限する。
BoidsSimulationクラス(シミュレーション全体の管理)
シミュレーション環境と可視化を管理する。
シミュレーション環境
- 空間サイズ:一辺52.0の立方体(各軸-26.0~+26.0)
- 個体数:500
- 境界処理:端から出た個体は反対側から再出現(トーラス型境界)
トーラス型境界とは、空間の端と端がつながっている境界条件である。
可視化
各個体を三角錐メッシュで表現する。先端が進行方向を向く。
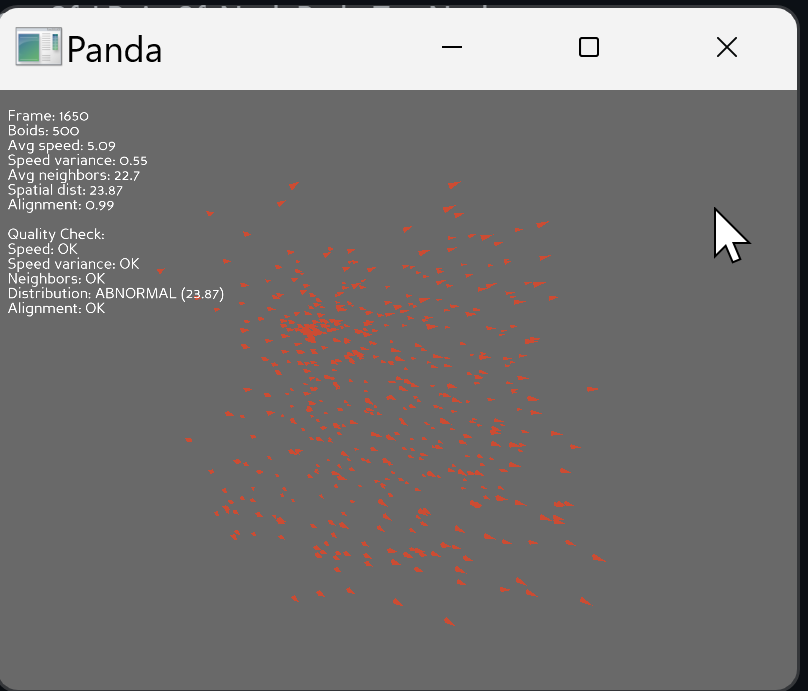
シミュレーション結果
観察される現象
プログラムを実行すると、最初はランダムな位置・方向にいた500個体が数秒で以下の動きを示す。
- 密集した群れの形成
- 群れ全体の協調的移動
- 群れの分裂と再結合の繰り返し
これらは3つのルールから自然に生まれる動きであり、明示的にプログラムしていない。
検証システム
シミュレーションの正常動作を確認するため、5つの指標を30フレームごとに計算し、画面左上に表示する。
指標1:平均速度
計算方法:全個体の速度の大きさを平均する。
意味:群れ全体の活動性。
判定基準:
- 2.0未満:停止に近い状態(異常)
- 2.0~8.0:適度な活動(正常)
- 8.0超:制御不能(異常)
指標2:速度分散
計算方法:各個体の速さと平均速度の差の2乗を平均する。
意味:個体間の速さのばらつき。値が小さいほど全個体が同じ速さで移動している。
判定基準:
- 3.0未満:均一な速度(正常)
- 3.0以上:速度のばらつきが大きい(異常)
指標3:平均近傍個体数
計算方法:各個体について、知覚半径10.0以内の他個体数を数え、全体で平均する。
意味:各個体が認識している仲間の数。群れの密集度を示す。
判定基準:
- 3未満:孤立個体が多い(異常)
- 3~30:適度な密集(正常)
- 30超:過密(異常)
指標4:空間分布
計算方法:全個体の位置の平均(重心)を計算し、各個体から重心までの距離を平均する。
意味:群れの広がり。値が小さいほど密集している。
判定基準:
- 3.0未満:過密(異常)
- 3.0~20.0:適度なまとまり(正常)
- 20.0超:広がりすぎ(異常)
指標5:整列スコア
計算方法:
- 各個体の速度ベクトルを長さ1に正規化(方向のみ抽出)
- 全個体の正規化ベクトルを合計
- 合計ベクトルの長さを個体数500で除算
意味:全個体の進行方向の一致度。1.0で全個体が同じ方向、0.0でランダムな方向を意味する。
判定基準:
- 0.3未満:方向がばらばら(異常)
- 0.3以上:方向が揃っている(正常)
品質評価
5つの指標がすべて正常範囲内にある場合、シミュレーションは現実の群れ行動を正しく再現していると判断できる。
アルゴリズムの意義
Boidsアルゴリズムの重要な点は、複雑な群れの動きが単純なルールから生まれることである。
各個体の行動:
- 周囲10.0以内の仲間のみを認識
- 3つのルール(離れる、合わせる、近づく)で方向を決定
群れ全体の振る舞い:
- 統一された方向への移動
- 障害物回避(分離ルールの応用)
- まとまりの維持
全体を制御する司令塔がなくても、個体の局所的な行動から全体の秩序が生まれる。この現象を自己組織化と呼ぶ。現実の鳥や魚の群れも同様の仕組みで動いていると考えられている。
演習
手順
- 3つの行動ルールの役割を把握する
- プログラムを実行し、500個体が群れを形成する過程を観察する
- 画面左上に表示される5つの指標を確認し、品質判定結果を記録する
注意点
知覚半径を小さくしすぎると、各個体が仲間を認識できず群れが形成されない。知覚半径を大きくしすぎると、計算負荷が高くなり動作が遅くなる。
from direct.showbase.ShowBase import ShowBase
from direct.task import Task
from panda3d.core import GeomVertexFormat, GeomVertexData, GeomVertexWriter
from panda3d.core import Geom, GeomTriangles, GeomNode, Mat4
from panda3d.core import LVector3f, LPoint3f, NodePath, TextNode
from direct.gui.OnscreenText import OnscreenText
import numpy as np
import random
import math
class BoidsSimulation(ShowBase):
def __init__(self):
ShowBase.__init__(self)
# 空間サイズ
self.space_size = 26.0
# 個体数
self.num_boids = 500
# Boidパラメータ
self.max_speed = 8.0
self.max_force = 0.4
self.perception_radius = 10.0
# NumPy配列で全個体の状態を管理
self.positions = np.random.uniform(-6.5, 6.5, (self.num_boids, 3))
self.velocities = np.random.uniform(-3, 3, (self.num_boids, 3))
self.accelerations = np.zeros((self.num_boids, 3))
# Visual representation for each boid (cone)
self.boid_nodes = []
for i in range(self.num_boids):
node = self.create_boid_mesh()
node_path = self.render.attachNewNode(node)
self.boid_nodes.append(node_path)
# Statistics initialization
self.frame_count = 0
self.metrics_history = {
'avg_speed': [],
'speed_variance': [],
'avg_neighbors': [],
'spatial_distribution': [],
'alignment_score': []
}
# Display statistics on screen
self.info_text = OnscreenText(
text='',
pos=(-1.3, 0.9),
scale=0.05,
fg=(1, 1, 1, 1),
align=TextNode.ALeft
)
# Camera setup(空間全体が見えるよう調整)
self.disableMouse()
self.camera.setPos(0, -120, 60)
self.camera.lookAt(0, 0, 0)
# 視野角を広げる
self.camLens.setFov(90)
mat = Mat4(self.camera.getMat())
mat.invertInPlace()
self.mouseInterfaceNode.setMat(mat)
self.enableMouse()
# Update task
self.taskMgr.add(self.update, "updateTask")
self.prev_time = globalClock.getFrameTime()
def create_boid_mesh(self):
"""Create cone mesh (visual representation of boid)"""
format = GeomVertexFormat.getV3n3c4()
vdata = GeomVertexData('boid', format, Geom.UHStatic)
vertex = GeomVertexWriter(vdata, 'vertex')
normal = GeomVertexWriter(vdata, 'normal')
color = GeomVertexWriter(vdata, 'color')
vertices = [
(0, 1, 0),
(-0.3, -0.5, 0.3),
(0.3, -0.5, 0.3),
(0, -0.5, -0.3)
]
for v in vertices:
vertex.addData3(*v)
normal.addData3(0, 1, 0)
color.addData4(0.8, 0.3, 0.2, 1.0)
tris = GeomTriangles(Geom.UHStatic)
tris.addVertices(0, 1, 2)
tris.addVertices(0, 2, 3)
tris.addVertices(0, 3, 1)
tris.addVertices(1, 3, 2)
geom = Geom(vdata)
geom.addPrimitive(tris)
node = GeomNode('boid_node')
node.addGeom(geom)
return node
def calculate_all_forces(self):
"""全個体の力を一括計算(NumPyベクトル化版)"""
n = self.num_boids
# 全ペア間の差分ベクトルを計算 (n, n, 3)
diff = self.positions[:, np.newaxis, :] - self.positions[np.newaxis, :, :]
# 全ペア間の距離を計算 (n, n)
distances = np.linalg.norm(diff, axis=2)
# 自分自身との距離を無限大に設定(除外用)
np.fill_diagonal(distances, np.inf)
# 知覚半径内のマスク (n, n)
in_range = distances < self.perception_radius
# 近傍個体数 (n,)
neighbor_counts = np.sum(in_range, axis=1)
# ゼロ除算防止
neighbor_counts_safe = np.where(neighbor_counts > 0, neighbor_counts, 1)
# --- 分離 (Separation) ---
# 距離の2乗で割った反発ベクトル
distances_safe = np.where(distances > 0, distances, 1)
separation_weights = np.where(in_range, 1.0 / (distances_safe ** 2), 0)
separation = np.sum(diff * separation_weights[:, :, np.newaxis], axis=1)
separation = separation / neighbor_counts_safe[:, np.newaxis]
# --- 整列 (Alignment) ---
# 近傍の速度の平均
velocity_masked = self.velocities[np.newaxis, :, :] * in_range[:, :, np.newaxis]
alignment = np.sum(velocity_masked, axis=1) / neighbor_counts_safe[:, np.newaxis]
# --- 結合 (Cohesion) ---
# 近傍の位置の平均(重心)への方向
position_masked = self.positions[np.newaxis, :, :] * in_range[:, :, np.newaxis]
center_of_mass = np.sum(position_masked, axis=1) / neighbor_counts_safe[:, np.newaxis]
cohesion = center_of_mass - self.positions
# ステアリング力に変換
separation_steering = self.steer(separation)
alignment_steering = self.steer(alignment)
cohesion_steering = self.steer(cohesion)
# 重み付け合成
total_force = separation_steering * 1.8 + alignment_steering * 1.5 + cohesion_steering * 1.8
# 近傍がいない個体は力をゼロに
total_force = np.where(neighbor_counts[:, np.newaxis] > 0, total_force, 0)
return total_force
def steer(self, desired):
"""目標方向へのステアリング力を計算"""
norms = np.linalg.norm(desired, axis=1, keepdims=True)
norms_safe = np.where(norms > 0, norms, 1)
# 目標速度
desired_normalized = (desired / norms_safe) * self.max_speed
# ステアリング = 目標速度 - 現在速度
steering = desired_normalized - self.velocities
# 最大力で制限
steering_norms = np.linalg.norm(steering, axis=1, keepdims=True)
steering_norms_safe = np.where(steering_norms > 0, steering_norms, 1)
steering = np.where(
steering_norms > self.max_force,
(steering / steering_norms_safe) * self.max_force,
steering
)
# 元のnormが0だった場合はゼロベクトル
steering = np.where(norms > 0, steering, 0)
return steering
def update_physics(self, dt):
"""物理更新"""
# 力を計算
forces = self.calculate_all_forces()
# 加速度を適用
self.velocities += forces * dt
# 速度制限
speeds = np.linalg.norm(self.velocities, axis=1, keepdims=True)
speeds_safe = np.where(speeds > 0, speeds, 1)
self.velocities = np.where(
speeds > self.max_speed,
(self.velocities / speeds_safe) * self.max_speed,
self.velocities
)
# 位置更新
self.positions += self.velocities * dt
# 境界条件(ラップアラウンド)
self.positions = np.where(
self.positions > self.space_size,
self.positions - 2 * self.space_size,
self.positions
)
self.positions = np.where(
self.positions < -self.space_size,
self.positions + 2 * self.space_size,
self.positions
)
def calculate_metrics(self):
"""Calculate simulation quality metrics"""
speeds = np.linalg.norm(self.velocities, axis=1)
avg_speed = np.mean(speeds)
speed_variance = np.var(speeds)
# 近傍個体数の計算
diff = self.positions[:, np.newaxis, :] - self.positions[np.newaxis, :, :]
distances = np.linalg.norm(diff, axis=2)
np.fill_diagonal(distances, np.inf)
in_range = distances < self.perception_radius
neighbor_counts = np.sum(in_range, axis=1)
avg_neighbors = np.mean(neighbor_counts)
# 空間分布
center = np.mean(self.positions, axis=0)
distances_from_center = np.linalg.norm(self.positions - center, axis=1)
spatial_distribution = np.mean(distances_from_center)
# 整列スコア
norms = np.linalg.norm(self.velocities, axis=1, keepdims=True)
norms_safe = np.where(norms > 0, norms, 1)
normalized = self.velocities / norms_safe
avg_velocity = np.sum(normalized, axis=0)
alignment_score = np.linalg.norm(avg_velocity) / self.num_boids
self.metrics_history['avg_speed'].append(avg_speed)
self.metrics_history['speed_variance'].append(speed_variance)
self.metrics_history['avg_neighbors'].append(avg_neighbors)
self.metrics_history['spatial_distribution'].append(spatial_distribution)
self.metrics_history['alignment_score'].append(alignment_score)
for key in self.metrics_history:
if len(self.metrics_history[key]) > 100:
self.metrics_history[key].pop(0)
return {
'avg_speed': avg_speed,
'speed_variance': speed_variance,
'avg_neighbors': avg_neighbors,
'spatial_distribution': spatial_distribution,
'alignment_score': alignment_score
}
def evaluate_quality(self, metrics):
"""Evaluate based on quality criteria"""
quality_checks = []
if 2.0 < metrics['avg_speed'] < 8.0:
quality_checks.append("Speed: OK")
else:
quality_checks.append(f"Speed: ABNORMAL ({metrics['avg_speed']:.2f})")
if metrics['speed_variance'] < 3.0:
quality_checks.append("Speed variance: OK")
else:
quality_checks.append(f"Speed variance: HIGH ({metrics['speed_variance']:.2f})")
if 3.0 < metrics['avg_neighbors'] < 30.0:
quality_checks.append("Neighbors: OK")
else:
quality_checks.append(f"Neighbors: ABNORMAL ({metrics['avg_neighbors']:.2f})")
if 3.0 < metrics['spatial_distribution'] < 20.0:
quality_checks.append("Distribution: OK")
else:
quality_checks.append(f"Distribution: ABNORMAL ({metrics['spatial_distribution']:.2f})")
if metrics['alignment_score'] > 0.3:
quality_checks.append("Alignment: OK")
else:
quality_checks.append(f"Alignment: LOW ({metrics['alignment_score']:.2f})")
return quality_checks
def update_visuals(self):
"""視覚表現の更新"""
speeds = np.linalg.norm(self.velocities, axis=1)
for i in range(self.num_boids):
# 位置を設定
self.boid_nodes[i].setPos(
float(self.positions[i, 0]),
float(self.positions[i, 1]),
float(self.positions[i, 2])
)
# 進行方向を向く
if speeds[i] > 0:
forward = self.velocities[i] / speeds[i]
target = self.positions[i] + forward
self.boid_nodes[i].lookAt(
LPoint3f(float(target[0]), float(target[1]), float(target[2]))
)
def update(self, task):
current_time = globalClock.getFrameTime()
dt = current_time - self.prev_time
self.prev_time = current_time
if dt < 0.0001:
return Task.cont
# 物理更新
self.update_physics(dt)
# 視覚更新
self.update_visuals()
self.frame_count += 1
if self.frame_count % 30 == 0:
metrics = self.calculate_metrics()
quality_checks = self.evaluate_quality(metrics)
info_lines = [
f"Frame: {self.frame_count}",
f"Boids: {self.num_boids}",
f"Avg speed: {metrics['avg_speed']:.2f}",
f"Speed variance: {metrics['speed_variance']:.2f}",
f"Avg neighbors: {metrics['avg_neighbors']:.1f}",
f"Spatial dist: {metrics['spatial_distribution']:.2f}",
f"Alignment: {metrics['alignment_score']:.2f}",
"",
"Quality Check:"
] + quality_checks
self.info_text.setText('\n'.join(info_lines))
return Task.cont
app = BoidsSimulation()
app.run()
流体シミュレーション(煙の拡散と上昇気流)

予備知識
流体力学と数値シミュレーション
煙や炎の動きは流体の運動として記述される。流体の運動を支配するナビエ・ストークス方程式は、質量保存則と運動量保存則から構成される偏微分方程式である。この方程式を厳密に解くことは困難なため、コンピュータで数値的に近似解を求める手法が用いられる。本プログラムではナビエ・ストークス方程式の簡易版を実装し、煙の基本的な挙動を再現する。
格子法による流体表現
流体シミュレーションには、空間を固定した格子で区切り各格子点での物理量を計算する格子法(オイラー法)と、流体を多数の粒子として扱う粒子法(ラグランジュ法)がある。格子法は計算が安定しやすく実装が比較的容易である。本プログラムは格子法を採用し、63×63×88の格子点で3次元空間を離散化する。各格子点には密度(煙の濃度を表す指標、0.0~1.0)と速度ベクトル(x、y、z方向の3成分)を記録する。格子間隔は0.5である。
流体シミュレーションの構成要素
流体シミュレーションは主に以下の物理過程で構成される。
- 移流:速度場に沿って物質(密度)や速度自体が移動する現象
- 拡散:濃度差や速度差が周囲に広がり平滑化される現象
- 外力:浮力など外部から加わる力
- 減衰:摩擦や散逸によりエネルギーが失われる現象
これらの過程を順次計算することで、流体の時間発展を模擬する。
実装例
Panda3Dで煙の拡散と上昇気流を可視化するプログラムである。63×63×88の3次元格子で流体場を表現し、格子間隔は0.5に設定する。密度場(3次元配列density)には各格子点での煙の濃度指標を0.0~1.0の範囲で記録する。速度場(3次元配列velocity_x、velocity_y、velocity_z)には各格子点での流体の速度ベクトルを記録する。パーティクルシステム(最大10000個)で煙を可視化し、各パーティクルは密度場と速度場に基づいて移動する。底面中央から継続的に煙が生成され、浮力により上昇しながら拡散する様子を観察できる。
物理パラメータ
シミュレーションの挙動を制御するパラメータを以下に示す。
- 拡散係数(diffusion):0.0002。煙の広がりやすさを制御する
- 粘性係数(viscosity):0.0001。速度場の拡散の度合いを制御する
- 浮力係数(buoyancy):0.3。密度値が高い領域に加わる上向きの力の大きさを制御する
- 減衰係数(dissipation):0.995。1フレームごとに密度が0.5%減少し、煙が徐々に薄くなる
移流の計算
移流はセミ・ラグランジュ法で計算する。通常の前進差分法(現在位置から速度方向に進んだ先の値を計算)は、速度が速いときや時間刻み幅が大きいときに数値的に不安定になり、値が発散する。セミ・ラグランジュ法では発想を逆転させる。ある格子点の新しい値を求める際、その点から速度ベクトルの逆方向に時間dtだけ遡った位置(出発点)を計算し、その出発点での値を新しい値とする。出発点を逆向きに探す操作をバックトレースと呼ぶ。バックトレースにより既存の値の範囲内に収まるため、数値的に安定である。
具体的な計算手順を以下に示す。
- 格子点(i, j, k)について、速度ベクトル(vx[i][j][k]、vy[i][j][k]、vz[i][j][k])を取得する
- 出発点の座標を計算する。x = i - dt × vx[i][j][k] / spacing × 10(y、zも同様)。係数10は移流の視覚的な速度を制御する調整値である
- 出発点の座標を格子範囲内に制限する
- 出発点が格子点上にない場合、周囲の格子点から3次元線形補間により値を求める
3次元線形補間では、出発点を囲む8個の格子点(立方体の頂点)の値を距離に応じて重み付け平均する。出発点に近い格子点ほど重みが大きい。出発点の座標を(x, y, z)とし、整数部分を(i0, j0, k0)、小数部分を(sx, sy, sz) = (x - i0, y - j0, z - k0)とする。各点の重みはx、y、z方向の距離の積で決まる。点(i0, j0, k0)の重みは(1-sx) × (1-sy) × (1-sz)、点(i0+1, j0, k0)の重みはsx × (1-sy) × (1-sz)となる。8点の値に重みを掛けて合計することで補間値が得られる。
拡散の計算
拡散は拡散方程式を離散化した連立1次方程式を解く。拡散方程式は∂u/∂t = α∇²uで表される。uは密度または速度成分、αは拡散係数、∇²はラプラシアン(2階微分演算子)である。陰解法で離散化すると以下の形になる。
(u_new - u_old) / dt = α × (周囲6点のu_newの和 - 6 × u_new) / h²
hは格子間隔である。整理すると次式を得る。
(1 + 6a) × u_new[i][j][k] = u_old[i][j][k] + a × (u_new[i-1][j][k] + u_new[i+1][j][k] + u_new[i][j-1][k] + u_new[i][j+1][k] + u_new[i][j][k-1] + u_new[i][j][k+1])
この連立方程式をガウス・ザイデル法で反復的に解く。各格子点について上式を変形した更新式を適用する。
u_new[i][j][k] = (u_old[i][j][k] + a × (周囲6点のu_newの和)) / (1 + 6a)
この更新を全格子点について繰り返すことで、解が真の解に近づく。本プログラムでは4回の反復で打ち切る。拡散により、密度や速度の局所的な偏りが周囲に広がる。
浮力の計算
各格子点の密度値に比例した上向きの力を速度場のz成分に加算する。
velocity_z[i][j][k] += buoyancy × density[i][j][k] × dt
この処理により、密度値が高い領域が上方に移動する。本プログラムでは温度を明示的に扱わず、密度値そのものを「周囲より高温な領域を示す指標」として扱う。密度値が高い格子点ほど上向きの力を受ける。
煙源の生成
底面中央(z = 0~2付近)の半径6の範囲に毎フレーム密度と速度を追加する。
- 密度を0.3増加させる(上限1.0)
- 上向き速度を3.0に設定する
- x、y方向にランダムな速度(-0.5~+0.5)を追加する
ランダムな横方向速度により、煙に自然な揺らぎが生まれる。
パーティクルシステムによる可視化
格子点の密度値だけでは煙の動きを視覚的に捉えにくい。そのため、10000個のパーティクル(小さな点)で煙を可視化する。各パーティクルは位置(x、y、z)、不透明度(alpha、0.0~1.0)、寿命(life、初期値450フレーム)の情報を持つ。
パーティクルの更新手順を以下に示す。
- パーティクルの位置から対応する格子点のインデックスを計算する
- その格子点の速度ベクトルを取得し、パーティクルを移動させる
- 格子点の密度値に基づいて不透明度を設定する。密度値が高い格子点にあるパーティクルほど不透明に表示される
- 寿命を1減らす。寿命が0になったパーティクルまたは空間外に出たパーティクルは削除する
新しいパーティクルは底面中央から毎フレーム最大100個生成される。パーティクルサイズは8ピクセルに設定する。パーティクルの色は明るさ = 0.7 + alpha × 0.3で計算され、不透明度が高いほど明るく表示される。
境界条件
格子の端(インデックス0およびgrid_size-1)では物理量の更新を行わない。内部の格子点(インデックス1~grid_size-2)のみを更新対象とする。境界での計算を省略することで、境界での数値的な不安定性を回避する。
計算の安定性
数値シミュレーションでは時間刻み幅dtが大きすぎると計算が不安定になる。本プログラムではdtの上限を0.05に制限することで安定性を確保する。CFL条件(Courant-Friedrichs-Lewy条件)と呼ばれる安定性条件では、移流計算において dt < h / v_max を満たす必要がある。hは格子間隔、v_maxは最大速度である。セミ・ラグランジュ法は前進差分法よりCFL条件に寛容であり、条件を多少超えても安定に動作する。
非圧縮性条件の省略
厳密な流体シミュレーションでは、速度場の発散をゼロにする非圧縮性条件を満たす必要がある。これには圧力場を計算し速度場を補正する投影(projection)ステップが必要である。本プログラムではこのステップを省略している。その結果、流体の体積が保存されず、局所的に膨張や収縮が発生する可能性がある。ただし煙のような視覚効果では、この影響は比較的小さく、省略しても自然な動きが得られる。
カメラ設定
カメラを位置(0, -65, 25)に配置し、空間中央やや上方の点(0, 0, 18)を注視する。背景色は黒(0, 0, 0)に設定し、白いパーティクルとのコントラストを高める。Panda3Dのデフォルトマウス操作(左クリックドラッグで回転、右クリックドラッグでズーム、中クリックドラッグで平行移動)が使用可能である。
実行結果
プログラムを実行すると、底面中央から白い煙が立ち上る。煙は浮力により上昇しながら、拡散により横方向に広がる。減衰により上層ほど煙は薄くなる。煙源から加えられるランダムな横方向速度により、煙に揺らぎが生まれ、複雑な流動パターンが形成される。セミ・ラグランジュ法による移流、ガウス・ザイデル法による拡散、浮力による上昇という物理過程の組み合わせにより、視覚的に自然な煙の動きが再現される。マウス操作でカメラを動かすことで、3次元的な煙の広がりを多角的に観察できる。
演習
手順
- プログラムを実行し、底面中央から煙が立ち上る様子を観察する
- 煙が浮力により上昇しながら拡散により横方向に広がる過程を観察する
- マウス操作でカメラを動かし、3次元的な煙の広がりを多角的に観察する
実行の前に、管理者権限でコマンドプロンプトを起動(手順:Windowsキーまたはスタートメニュー > cmd と入力 > 右クリック > 「管理者として実行」)し、以下を実行する。管理者権限は、wingetの--scope machineオプションでシステム全体にソフトウェアをインストールするために必要である。
pip install numba
from direct.showbase.ShowBase import ShowBase
from direct.task import Task
from panda3d.core import GeomVertexFormat, GeomVertexData, GeomVertexWriter
from panda3d.core import Mat4, PointLight, AmbientLight, VBase4
from panda3d.core import Geom, GeomTriangles, GeomNode, GeomPoints
from panda3d.core import Point3, Vec3, RenderModeAttrib
import numpy as np
from numba import jit, prange
import random
import math
# Numba JITコンパイル関数(モジュールレベルで定義)
@jit(nopython=True, parallel=True, cache=True)
def advect_numba(field, vx, vy, vz, dt, spacing, gx, gy, gz):
"""移流:速度場に沿ってフィールド値を移動(Numba版)"""
new_field = np.zeros_like(field)
for i in prange(1, gx - 1):
for j in range(1, gy - 1):
for k in range(1, gz - 1):
# バックトレース
x = i - dt * vx[i, j, k] / spacing * 10
y = j - dt * vy[i, j, k] / spacing * 10
z = k - dt * vz[i, j, k] / spacing * 10
# 境界内にクランプ
x = max(0.5, min(gx - 1.5, x))
y = max(0.5, min(gy - 1.5, y))
z = max(0.5, min(gz - 1.5, z))
# 線形補間のためのインデックス
i0 = int(x)
j0 = int(y)
k0 = int(z)
i1 = min(i0 + 1, gx - 1)
j1 = min(j0 + 1, gy - 1)
k1 = min(k0 + 1, gz - 1)
sx = x - i0
sy = y - j0
sz = z - k0
# 3次元線形補間
new_field[i, j, k] = (
field[i0, j0, k0] * (1-sx) * (1-sy) * (1-sz) +
field[i1, j0, k0] * sx * (1-sy) * (1-sz) +
field[i0, j1, k0] * (1-sx) * sy * (1-sz) +
field[i0, j0, k1] * (1-sx) * (1-sy) * sz +
field[i1, j1, k0] * sx * sy * (1-sz) +
field[i1, j0, k1] * sx * (1-sy) * sz +
field[i0, j1, k1] * (1-sx) * sy * sz +
field[i1, j1, k1] * sx * sy * sz
)
return new_field
@jit(nopython=True, parallel=True, cache=True)
def diffuse_numba(field, diff_rate, dt, gx, gy, gz, iterations=4):
"""拡散:フィールド値の平滑化(Numba版)"""
avg_size = (gx + gy + gz) / 3
a = dt * diff_rate * (avg_size - 2) ** 2
new_field = field.copy()
for _ in range(iterations):
for i in prange(1, gx - 1):
for j in range(1, gy - 1):
for k in range(1, gz - 1):
new_field[i, j, k] = (
field[i, j, k] + a * (
new_field[i-1, j, k] + new_field[i+1, j, k] +
new_field[i, j-1, k] + new_field[i, j+1, k] +
new_field[i, j, k-1] + new_field[i, j, k+1]
)
) / (1 + 6 * a)
return new_field
@jit(nopython=True, parallel=True, cache=True)
def add_buoyancy_numba(velocity_z, density, buoyancy, dt):
"""浮力の追加(Numba版)"""
gx, gy, gz = velocity_z.shape
for i in prange(gx):
for j in range(gy):
for k in range(gz):
velocity_z[i, j, k] += buoyancy * density[i, j, k] * dt
return velocity_z
@jit(nopython=True, cache=True)
def apply_dissipation_numba(density, dissipation):
"""減衰(Numba版)"""
gx, gy, gz = density.shape
for i in range(gx):
for j in range(gy):
for k in range(gz):
density[i, j, k] *= dissipation
return density
class FluidSimulation(ShowBase):
def __init__(self):
ShowBase.__init__(self)
# 背景色を黒に設定
self.setBackgroundColor(0, 0, 0)
# グリッドサイズ(体積2倍:63×63×88)
self.grid_size_x = 63
self.grid_size_y = 63
self.grid_size_z = 88
self.spacing = 0.5
# 流体密度場(煙の濃度)- NumPy配列
self.density = np.zeros((self.grid_size_x, self.grid_size_y, self.grid_size_z), dtype=np.float64)
# 速度場(3次元ベクトル場)- NumPy配列
self.velocity_x = np.zeros((self.grid_size_x, self.grid_size_y, self.grid_size_z), dtype=np.float64)
self.velocity_y = np.zeros((self.grid_size_x, self.grid_size_y, self.grid_size_z), dtype=np.float64)
self.velocity_z = np.zeros((self.grid_size_x, self.grid_size_y, self.grid_size_z), dtype=np.float64)
# シミュレーションパラメータ
self.diffusion = 0.0002
self.viscosity = 0.0001
self.buoyancy = 0.3
self.dissipation = 0.995
# パーティクルシステム(体積2倍に合わせて増加:10000個)
self.particles = []
self.max_particles = 10000
# パーティクルメッシュの作成
self.particle_mesh = self.create_particle_mesh()
self.particle_node = self.render.attachNewNode(self.particle_mesh)
self.particle_node.setPos(
-self.grid_size_x * self.spacing / 2,
-self.grid_size_y * self.spacing / 2,
0
)
# パーティクルサイズを大きく設定
self.particle_node.setRenderMode(RenderModeAttrib.MPoint, 8.0)
# ライティング設定
alight = AmbientLight('alight')
alight.setColor(VBase4(0.3, 0.3, 0.3, 1))
alnp = self.render.attachNewNode(alight)
self.render.setLight(alnp)
# カメラ設定(空間サイズに合わせて調整)
self.disableMouse()
self.camera.setPos(0, -65, 25)
self.camera.lookAt(0, 0, 18)
self.camLens.setFov(80)
mat = Mat4(self.camera.getMat())
mat.invertInPlace()
self.mouseInterfaceNode.setMat(mat)
self.enableMouse()
# JITコンパイルのウォームアップ(初回実行時のコンパイル遅延を回避)
self.warmup_jit()
self.taskMgr.add(self.update, "updateTask")
self.prev_time = globalClock.getFrameTime()
self.frame_count = 0
def warmup_jit(self):
"""JITコンパイルのウォームアップ"""
# 小さな配列でコンパイルを事前実行
small = np.zeros((5, 5, 5), dtype=np.float64)
advect_numba(small, small, small, small, 0.01, 0.5, 5, 5, 5)
diffuse_numba(small, 0.0001, 0.01, 5, 5, 5)
add_buoyancy_numba(small.copy(), small, 0.3, 0.01)
apply_dissipation_numba(small.copy(), 0.995)
def create_particle_mesh(self):
"""パーティクル可視化用のメッシュ作成"""
format = GeomVertexFormat.getV3c4()
vdata = GeomVertexData('particles', format, Geom.UHDynamic)
vertex = GeomVertexWriter(vdata, 'vertex')
color = GeomVertexWriter(vdata, 'color')
# 初期パーティクルの配置
for _ in range(self.max_particles):
vertex.addData3(0, 0, 0)
color.addData4(1.0, 1.0, 1.0, 0.0)
points = GeomPoints(Geom.UHDynamic)
points.addNextVertices(self.max_particles)
geom = Geom(vdata)
geom.addPrimitive(points)
node = GeomNode('particle_node')
node.addGeom(geom)
return node
def add_smoke_source(self):
"""煙源の追加"""
center_x = self.grid_size_x // 2
center_y = self.grid_size_y // 2
radius = 6
for i in range(center_x - radius, center_x + radius):
for j in range(center_y - radius, center_y + radius):
dist = math.sqrt((i - center_x)**2 + (j - center_y)**2)
if dist < radius:
for k in range(0, 3):
if 0 <= i < self.grid_size_x and 0 <= j < self.grid_size_y:
self.density[i, j, k] = min(1.0, self.density[i, j, k] + 0.3)
self.velocity_z[i, j, k] = 3.0
self.velocity_x[i, j, k] += random.uniform(-0.5, 0.5)
self.velocity_y[i, j, k] += random.uniform(-0.5, 0.5)
def update_fluid(self, dt):
"""流体シミュレーションの更新(Numba版)"""
dt = min(dt, 0.05)
gx, gy, gz = self.grid_size_x, self.grid_size_y, self.grid_size_z
# 1. 浮力の追加
self.velocity_z = add_buoyancy_numba(self.velocity_z, self.density, self.buoyancy, dt)
# 2. 速度場の拡散
self.velocity_x = diffuse_numba(self.velocity_x, self.viscosity, dt, gx, gy, gz)
self.velocity_y = diffuse_numba(self.velocity_y, self.viscosity, dt, gx, gy, gz)
self.velocity_z = diffuse_numba(self.velocity_z, self.viscosity, dt, gx, gy, gz)
# 3. 速度場の移流
self.velocity_x = advect_numba(self.velocity_x, self.velocity_x, self.velocity_y, self.velocity_z, dt, self.spacing, gx, gy, gz)
self.velocity_y = advect_numba(self.velocity_y, self.velocity_x, self.velocity_y, self.velocity_z, dt, self.spacing, gx, gy, gz)
self.velocity_z = advect_numba(self.velocity_z, self.velocity_x, self.velocity_y, self.velocity_z, dt, self.spacing, gx, gy, gz)
# 4. 密度場の拡散
self.density = diffuse_numba(self.density, self.diffusion, dt, gx, gy, gz)
# 5. 密度場の移流
self.density = advect_numba(self.density, self.velocity_x, self.velocity_y, self.velocity_z, dt, self.spacing, gx, gy, gz)
# 6. 減衰
self.density = apply_dissipation_numba(self.density, self.dissipation)
# 7. 煙源の追加
self.add_smoke_source()
def update_particles(self):
"""パーティクル位置の更新"""
gx, gy, gz = self.grid_size_x, self.grid_size_y, self.grid_size_z
# 既存パーティクルの更新
for particle in self.particles[:]:
i = int(particle['x'] / self.spacing)
j = int(particle['y'] / self.spacing)
k = int(particle['z'] / self.spacing)
if 0 <= i < gx - 1 and 0 <= j < gy - 1 and 0 <= k < gz - 1:
# 速度場からパーティクルの移動
particle['x'] += self.velocity_x[i, j, k] * 0.05
particle['y'] += self.velocity_y[i, j, k] * 0.05
particle['z'] += self.velocity_z[i, j, k] * 0.05
# 密度に基づいて不透明度を設定
particle['alpha'] = min(1.0, self.density[i, j, k] * 1.5)
particle['life'] -= 1
else:
particle['life'] = 0
if particle['life'] <= 0 or particle['z'] > gz * self.spacing:
self.particles.remove(particle)
# 新しいパーティクルの追加
if len(self.particles) < self.max_particles:
center_x = self.grid_size_x // 2
center_y = self.grid_size_y // 2
for _ in range(min(100, self.max_particles - len(self.particles))):
x = (center_x + random.uniform(-5, 5)) * self.spacing
y = (center_y + random.uniform(-5, 5)) * self.spacing
z = random.uniform(0, 1) * self.spacing
self.particles.append({
'x': x, 'y': y, 'z': z,
'alpha': 0.8,
'life': 450
})
def update_mesh(self):
"""パーティクルメッシュの更新"""
geom = self.particle_mesh.modifyGeom(0)
vdata = geom.modifyVertexData()
vertex = GeomVertexWriter(vdata, 'vertex')
color = GeomVertexWriter(vdata, 'color')
# パーティクルデータの書き込み
for i, particle in enumerate(self.particles):
if i >= self.max_particles:
break
vertex.setData3(particle['x'], particle['y'], particle['z'])
alpha = particle['alpha']
# グレーから白へのグラデーション
brightness = 0.7 + alpha * 0.3
color.setData4(brightness, brightness, brightness, alpha)
# 残りのパーティクルは透明に
for i in range(len(self.particles), self.max_particles):
vertex.setData3(0, 0, 0)
color.setData4(0, 0, 0, 0)
def update(self, task):
current_time = globalClock.getFrameTime()
dt = current_time - self.prev_time
self.prev_time = current_time
if dt < 0.0001:
return Task.cont
self.update_fluid(dt)
self.update_particles()
self.update_mesh()
self.frame_count += 1
return Task.cont
app = FluidSimulation()
app.run()
![[kaneko lab.]](https://www.kkaneko.jp/info/logo_png.png)