ニューラルネットワークと機械学習の基礎：概念からPyTorchによる実装まで

【概要】

ニューラルネットワークは、ニューロンを処理単位として構成される機械学習モデルである。各ニューロンは、入力の重みづけ、重み付き和とバイアスの加算、活性化関数の適用を行う。PyTorchを用いた実装では、訓練データによる学習を通じて、ニューロン間の結合の重みとバイアスを最適化し、データの特徴やパターンを獲得する。学習では、バックプロパゲーションによる誤差の逆伝播と、勾配降下法による誤差の最小化が中心的な役割を担う。

【本資料の読み方】

第2章で機械学習とMNISTの概要を示し、第3章では完成プログラム（演習1）を実行する。これは本資料が最終的に到達する内容のデモであり、ここで用いる用語やコードの細部（バッチ、エポック、損失関数など）がこの時点で分からなくても差し支えない。第4章以降で、ニューロン、活性化関数、フォワードプロパゲーション、バックプロパゲーションを順に説明する。これらを理解したうえで第3章のプログラムに戻ると、全体像が把握できる構成である。

ニューラルネットワークの学習では、出力と正解のずれを測る損失関数をタスクに応じて使い分ける。分類タスク（MNISTなど、入力をいずれかのクラスに振り分ける問題）では交差エントロピーを、第8章の手計算例のような単純な数値合わせでは二乗誤差を用いる。用語は以下のように使い分ける。損失（loss）は損失関数が出力する1つの数値で、出力全体のずれを集約した値である。誤差（error）は出力と正解の各要素のずれを指す。勾配（gradient）は、損失を小さくするために各重み・バイアスをどの向きにどれだけ変えればよいかを示す量であり、バックプロパゲーションで計算される。

【目次】

1. PythonとPyTorchのインストール（Windows上）
2. 機械学習の概要とPyTorchによる実装例
3. 演習1．MNISTの学習と正解率の確認
4. ニューラルネットワークの基本構造と仕組み
5. 活性化関数とその役割
6. ニューラルネットワークの構造とフォワードプロパゲーション
7. バックプロパゲーションと学習メカニズム
8. 演習2．二乗誤差による重みの更新
9. 過学習の概念と対策
10. ディープラーニングの概要
11. まとめ

1. PythonとPyTorchのインストール（Windows上）

Python 3.12 のインストール

Pythonのインストールを行い、Pythonのプログラムを実行する環境を整える。扱う環境は、Windows搭載パソコンである。金子研究室では、Python 3.12.10を推奨する。

[Windows での Python 3.12 のインストール手順を見るには、ここをクリック]

Windows での Python 3.12 のインストール

以下のいずれかの方法でPython 3.12をインストールする。Pythonがインストール済みの場合、この手順は不要である。

方法 1：winget によるインストール

【インストールコマンドの実行方法】

管理者権限でコマンドプロンプトを起動する（手順：Windowsキーまたはスタートメニュー → cmd と入力 → 右クリック → 「管理者として実行」）。そして、コマンド全体をコマンドプロンプトにコピー＆ペーストする。

--scope machine を指定することで、システム全体（全ユーザー向け）にインストールされる。このオプションの実行には管理者権限が必要である。インストール完了後、コマンドプロンプトを再起動するとPATHが反映される。

REM Python 3.12 をシステム領域にインストール
winget install --id Python.Python.3.12 -e --scope machine --silent --accept-source-agreements --accept-package-agreements --override "/quiet InstallAllUsers=1 PrependPath=1 Include_test=0 Include_pip=1 Include_launcher=1 InstallLauncherAllUsers=1 TargetDir=\"C:\Program Files\Python312\""
if not "%ERRORLEVEL%"=="0" ( color 0c & echo Python 3.12 のインストールに失敗しました & ping 127.0.0.1 -n 6 >nul & color )

REM Python と Scripts を PATH 先頭に追加
powershell -NoProfile -Command "$p='C:\Program Files\Python312'; $s=\"$p\Scripts\"; if(Test-Path $p){$k=[Microsoft.Win32.Registry]::LocalMachine.OpenSubKey('SYSTEM\CurrentControlSet\Control\Session Manager\Environment',$true); $c=$k.GetValue('Path','',[Microsoft.Win32.RegistryValueOptions]::DoNotExpandEnvironmentNames); $t=$k.GetValueKind('Path'); $new=$c; if((';'+$new+';') -notlike \"*;$p;*\"){$new=$p+';'+$new}; if((';'+$new+';') -notlike \"*;$s;*\"){$new=$s+';'+$new}; if($new -ne $c){$k.SetValue('Path',$new,$t)}; $k.Close()}"

REM 現在のセッションにも反映（システムPATHを再取得して連結）
for /f "usebackq tokens=2,*" %A in (`reg query "HKLM\SYSTEM\CurrentControlSet\Control\Session Manager\Environment" /v Path`) do set "PATH=%B"

REM pip / wheel の更新
python -m pip install --no-user -U pip wheel
if not "%ERRORLEVEL%"=="0" ( color 0c & echo pip / wheel の更新に失敗しました & ping 127.0.0.1 -n 6 >nul & color )

方法 2：インストーラーによるインストール

Python公式サイト（https://www.python.org/downloads/）にアクセスし、「Download Python 3.x.x」ボタンからWindows用インストーラーをダウンロードする。
ダウンロードしたインストーラーを実行する。
初期画面の下部に表示される「Add python.exe to PATH」にチェックを入れてから「Customize installation」を選択する。このチェックを入れ忘れると、コマンドプロンプトから python コマンドを実行できない。
「Install Python 3.xx for all users」にチェックを入れ、「Install」をクリックする。

インストールの確認

コマンドプロンプトで以下を実行する。

python --version

バージョン番号（例：Python 3.12.x）が表示されればインストール成功である。「'python' は、内部コマンドまたは外部コマンドとして認識されていません。」と表示される場合は、インストールが正常に完了していない。

Build Tools・CUDA Toolkit・PyTorch のインストール

本章では、C++ ビルドツール、NVIDIA CUDA Toolkit、PyTorch のインストールを行い、GPU を活用した機械学習プログラムを実行する環境を整える。扱う環境は、Windows 搭載パソコンである。

[Build Tools・CUDA Toolkit・PyTorch のインストール手順を見るには、ここをクリック]

Windows での Build Tools for Visual Studio 2026 のインストール

Build Tools for Visual Studio 2026 は、C++ ソースコードを Windows 用バイナリにコンパイルするための開発ツール群である。unsloth 等の一部 Python パッケージは、インストール時に C++ コードのビルドを必要とするため、これらのツールが必須となる。

以下のコマンドは、Build Tools が未インストールの場合は winget で新規インストールし、インストール済みの場合は setup.exe modify でコンポーネントを追加する（バージョンは変更しない）。

【インストールコマンドの実行方法】

管理者権限でコマンドプロンプトを起動する（手順：Windows キーまたはスタートメニュー → cmd と入力 → 右クリック → 「管理者として実行」）。そして、コマンド全体をコマンドプロンプトにコピー＆ペーストする。

REM ============================================================
REM Visual C++ 再頒布可能パッケージ (VCRedist 2015-)
REM ============================================================
winget install --scope machine --id Microsoft.VCRedist.2015+.x64 -e --silent --disable-interactivity --force --accept-source-agreements --accept-package-agreements --override "/quiet /norestart"
if not "%ERRORLEVEL%"=="0" ( color 0c & echo VCRedist のインストールに失敗しました & ping 127.0.0.1 -n 6 >nul & color )

REM ============================================================
REM Visual Studio Build Tools + Desktop development with C++
REM （VCTools、MSBuildTools、CMake連携、Clang、Windows 11 SDK）
REM ============================================================
REM 進行中のインストーラーを停止（ロック競合回避。対象プロセスが存在しない場合は
REM taskkillがエラーを返すが、これは想定内であるため出力のみ抑制する）
taskkill /F /IM vs_setup.exe /T >nul 2>&1
taskkill /F /IM vs_installer.exe /T >nul 2>&1
taskkill /F /IM vs_installerservice.exe /T >nul 2>&1
taskkill /F /IM msiexec.exe /T >nul 2>&1

REM Build Tools + Desktop development with C++（VCTools）+ 追加コンポーネント（一括）
REM 未インストール時: winget で新規インストール
REM インストール済み時: setup.exe modify でコンポーネント追加（バージョンは変更しない）
winget list --id Microsoft.VisualStudio.BuildTools 2>nul | findstr /i "BuildTools" >nul 2>&1
if %ERRORLEVEL% EQU 0 (
    for /f "usebackq delims=" %P in (`"C:\Program Files (x86)\Microsoft Visual Studio\Installer\vswhere.exe" -products Microsoft.VisualStudio.Product.BuildTools -property installationPath`) do start /wait "" "C:\Program Files (x86)\Microsoft Visual Studio\Installer\setup.exe" modify --installPath "%P" --add Microsoft.VisualStudio.Workload.VCTools --add Microsoft.VisualStudio.Workload.MSBuildTools --add Microsoft.VisualStudio.Component.VC.CMake.Project --add Microsoft.VisualStudio.Component.VC.Llvm.Clang --add Microsoft.VisualStudio.Component.VC.Llvm.ClangToolset --add Microsoft.VisualStudio.Component.Windows11SDK.26100 --add Microsoft.VisualStudio.Component.VC.v143.x86.x64 --includeRecommended --quiet --norestart --nocache
    if not "%ERRORLEVEL%"=="0" ( color 0c & echo Build Tools のコンポーネント追加に失敗しました & ping 127.0.0.1 -n 6 >nul & color )
) else (
    winget install --scope machine --id Microsoft.VisualStudio.BuildTools -e --silent --disable-interactivity --force --accept-source-agreements --accept-package-agreements --override "--quiet --wait --norestart --nocache --add Microsoft.VisualStudio.Workload.VCTools --includeRecommended --add Microsoft.VisualStudio.Workload.MSBuildTools --add Microsoft.VisualStudio.Component.VC.CMake.Project --add Microsoft.VisualStudio.Component.VC.Llvm.Clang --add Microsoft.VisualStudio.Component.VC.Llvm.ClangToolset --add Microsoft.VisualStudio.Component.Windows11SDK.26100 --add Microsoft.VisualStudio.Component.VC.v143.x86.x64"
    if not "%ERRORLEVEL%"=="0" ( color 0c & echo Build Tools のインストールに失敗しました & ping 127.0.0.1 -n 6 >nul & color )
)

REM BuildTools のインストールパスを vswhere.exe で取得（メジャーバージョンに依存しない）
set "VSWHERE=C:\Program Files (x86)\Microsoft Visual Studio\Installer\vswhere.exe"
set "BT_PATH="
for /f "usebackq delims=" %P in (`"%VSWHERE%" -products Microsoft.VisualStudio.Product.BuildTools -property installationPath`) do set "BT_PATH=%P"
if not defined BT_PATH ( color 0c & echo Build Tools のインストールパスを取得できませんでした & ping 127.0.0.1 -n 6 >nul & color )

REM 破損時の修復（任意、動作がおかしくなった場合）
REM if defined BT_PATH "C:\Program Files (x86)\Microsoft Visual Studio\Installer\setup.exe" repair --installPath "%BT_PATH%" --quiet --norestart
REM 導入確認（インストールパスが表示されれば正常）
"%VSWHERE%" -products * -requires Microsoft.VisualStudio.Workload.VCTools -property installationPath

上記のコマンドでは、Build Tools 本体と Visual C++ 再頒布可能パッケージをインストールし、続いて以下のコンポーネントを追加している。

VCTools：C++ デスクトップ開発ワークロード（--includeRecommended により、MSVC コンパイラ、C++ AddressSanitizer、vcpkg、CMake ツール、Windows 11 SDK 等の推奨コンポーネントが含まれる）
MSBuildTools：MSBuild によるビルドツールのワークロード
VC.CMake.Project：Windows 向け C++ CMake ツール
VC.Llvm.Clang：Windows 向け C++ Clang コンパイラ
VC.Llvm.ClangToolset：MSBuild から Clang を使用するための clang-cl ツールセット
Windows11SDK.26100：Windows 11 SDK（ビルド 10.0.26100）

追加のコンポーネントが必要になった場合は Visual Studio Installer で個別にインストールできる。

Windows での NVIDIA CUDA Toolkit のインストール

NVIDIA CUDA Toolkit は、NVIDIA GPU 上で計算を行うためのコンパイラ・ライブラリ群である。PyTorch や vLLM 等が GPU を利用するために必要となる。GPU を使用しない場合、この手順は不要である。

前提条件：NVIDIA GPU、NVIDIA ドライバ、Build Tools for Visual Studio もしくは Visual Studio が必要である。

インストール中の注意：他のウインドウは閉じておくこと。

【インストールコマンドの実行方法】

管理者権限でコマンドプロンプトを起動する（手順：Windows キーまたはスタートメニュー → cmd と入力 → 右クリック → 「管理者として実行」）。そして、コマンド全体をコマンドプロンプトにコピー＆ペーストする。

REM ============================================================
REM CUDA 12.8
REM ============================================================
winget install --scope machine --id Nvidia.CUDA --version 12.8 -e --silent --disable-interactivity --force --uninstall-previous --accept-source-agreements --accept-package-agreements --override "-s -n"
if not "%ERRORLEVEL%"=="0" ( color 0c & echo CUDA のインストールに失敗しました & ping 127.0.0.1 -n 6 >nul & color )

REM 統合用ファイルのコピー
if exist "C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v12.8\" (
    xcopy "C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v12.8\extras\visual_studio_integration\MSBuildExtensions\*.*" "c:\Program Files\Microsoft Visual Studio\18\Community\MSBuild\Microsoft\VC\v180\BuildCustomizations\" /Y
    xcopy "C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v12.8\extras\visual_studio_integration\MSBuildExtensions\*.*" "C:\Program Files (x86)\Microsoft Visual Studio\18\BuildTools\MSBuild\Microsoft\VC\v180\BuildCustomizations\" /Y
    xcopy "C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v12.8\extras\visual_studio_integration\MSBuildExtensions\*.*" "C:\Program Files (x86)\Microsoft Visual Studio\18\BuildTools\MSBuild\Microsoft\VC\v170\BuildCustomizations\" /Y /I
) else (
    echo CUDA v12.8 のディレクトリが存在しません。
    ping 127.0.0.1 -n 6 >nul
)

REM 環境変数TEMP, TMPの設定（一時ファイルの保存先を短いパスに変更）
set "TEMP=C:\TEMP"
set "TMP=C:\TEMP"
powershell -NoProfile -Command "$k=[Microsoft.Win32.Registry]::LocalMachine.OpenSubKey('SYSTEM\CurrentControlSet\Control\Session Manager\Environment',$true); foreach($n in @('TEMP','TMP')){ $t=[Microsoft.Win32.RegistryValueKind]::ExpandString; if($k.GetValueNames() -contains $n){ $t=$k.GetValueKind($n) }; $k.SetValue($n,'C:\TEMP',$t) }; $k.Close()"
reg query "HKLM\SYSTEM\CurrentControlSet\Control\Session Manager\Environment" /v TEMP
reg query "HKLM\SYSTEM\CurrentControlSet\Control\Session Manager\Environment" /v TMP

環境変数 TEMP および TMP を C:\TEMP に変更しているのは、後続のインストール処理で長いパス名や空白を含むパス名がエラーの原因となる場合があるためである。

Windows での PyTorch のインストール

https://pytorch.org のインストールガイドに従い、自環境の CUDA バージョンに対応したコマンドを取得して実行する。CUDA バージョンは以下で確認できる。

nvcc --version

管理者権限でコマンドプロンプトを起動し、以下を実行する。cu128 は CUDA 12.8 用のタグである。CUDA バージョンが異なる場合は、上記公式サイトで該当するタグを確認し、URL 末尾の cu128 を置き換えること。

REM numpy と PyTorch（CUDA 12.8 対応 wheel）、pip キャッシュを全削除
set "CUDA_TAG=cu128"
pip install --no-user -U numpy torch torchvision torchaudio --index-url https://download.pytorch.org/whl/%CUDA_TAG%
if not "%ERRORLEVEL%"=="0" ( color 0c & echo numpy / PyTorch のインストールに失敗しました & ping 127.0.0.1 -n 6 >nul & color )

Python の開発環境 Visual Studio Code のインストールと Python 用の設定

Python の開発環境Visual Studio Code（プログラムを編集するソフトウェア。以下、VS Code）を整える。

[Windows での Visual Studio Code のインストールと Python 用の設定手順を見るには、ここをクリック]

Windows での Visual Studio Code のインストールと Python 用の設定手順

1. VS Code と拡張機能のインストール

以下のコマンドにより，既存の VS Code を削除し，全ユーザー共有の設定で再インストールしたうえで，拡張機能（VS Code に機能を追加するソフトウェア）をまとめて導入する．

【インストールコマンドの実行方法】

管理者権限でコマンドプロンプトを起動する（手順：Windows キーまたはスタートメニュー → cmd と入力 → 右クリック → 「管理者として実行」）。そして，コマンド全体をコマンドプロンプトにコピー＆ペーストする。

インストールコマンド


REM ============================================================
REM Microsoft Visual Studio Code
REM ============================================================
REM Build Tools + Desktop development with C++（VCTools）+ 追加コンポーネント（一括）
REM 未インストール時: winget で新規インストール
REM インストール済み時: setup.exe modify でコンポーネント追加（バージョンは変更しない）
winget list --id Microsoft.VisualStudio.BuildTools 2>nul | findstr /i "BuildTools" >nul 2>&1
if %ERRORLEVEL% EQU 0 (
    for /f "usebackq delims=" %P in (`"C:\Program Files (x86)\Microsoft Visual Studio\Installer\vswhere.exe" -products Microsoft.VisualStudio.Product.BuildTools -property installationPath`) do start /wait "" "C:\Program Files (x86)\Microsoft Visual Studio\Installer\setup.exe" modify --installPath "%P" --add Microsoft.VisualStudio.Workload.VCTools --add Microsoft.VisualStudio.Workload.MSBuildTools --add Microsoft.VisualStudio.Component.VC.CMake.Project --add Microsoft.VisualStudio.Component.VC.Llvm.Clang --add Microsoft.VisualStudio.Component.VC.Llvm.ClangToolset --add Microsoft.VisualStudio.Component.Windows11SDK.26100 --add Microsoft.VisualStudio.Component.VC.v143.x86.x64 --includeRecommended --quiet --norestart --nocache
    if not "%ERRORLEVEL%"=="0" ( color 0c & echo Build Tools のコンポーネント追加に失敗しました & ping 127.0.0.1 -n 6 >nul & color )
) else (
    winget install --scope machine --id Microsoft.VisualStudio.BuildTools -e --silent --disable-interactivity --force --accept-source-agreements --accept-package-agreements --override "--quiet --wait --norestart --nocache --add Microsoft.VisualStudio.Workload.VCTools --includeRecommended --add Microsoft.VisualStudio.Workload.MSBuildTools --add Microsoft.VisualStudio.Component.VC.CMake.Project --add Microsoft.VisualStudio.Component.VC.Llvm.Clang --add Microsoft.VisualStudio.Component.VC.Llvm.ClangToolset --add Microsoft.VisualStudio.Component.Windows11SDK.26100 --add Microsoft.VisualStudio.Component.VC.v143.x86.x64"
    if not "%ERRORLEVEL%"=="0" ( color 0c & echo Build Tools のインストールに失敗しました & ping 127.0.0.1 -n 6 >nul & color )
)

REM 全ユーザー共有の拡張機能フォルダ
if not exist "C:\ProgramData\vscode-extensions" mkdir "C:\ProgramData\vscode-extensions"
icacls "C:\ProgramData\vscode-extensions" /grant "Everyone:(OI)(CI)M" /T

REM スタートメニューのショートカットを --extensions-dir 付きで再作成
if exist "C:\ProgramData\Microsoft\Windows\Start Menu\Programs\Visual Studio Code" rmdir /s /q "C:\ProgramData\Microsoft\Windows\Start Menu\Programs\Visual Studio Code"
if exist "C:\ProgramData\Microsoft\Windows\Start Menu\Programs\Visual Studio Code.lnk" del "C:\ProgramData\Microsoft\Windows\Start Menu\Programs\Visual Studio Code.lnk"
powershell -NoProfile -Command "$s=New-Object -ComObject WScript.Shell; $lnk=$s.CreateShortcut('C:\ProgramData\Microsoft\Windows\Start Menu\Programs\Visual Studio Code.lnk'); $lnk.TargetPath='C:\Program Files\Microsoft VS Code\Code.exe'; $lnk.Arguments='--extensions-dir \"C:\ProgramData\vscode-extensions\"'; $lnk.Save()"
REM ショートカットの検証
powershell -NoProfile -Command "$s=New-Object -ComObject WScript.Shell; $lnk=$s.CreateShortcut('C:\ProgramData\Microsoft\Windows\Start Menu\Programs\Visual Studio Code.lnk'); Write-Host 'TargetPath:' $lnk.TargetPath; Write-Host 'Arguments:' $lnk.Arguments"

REM ファイル / フォルダ右クリックの「Code で開く」を登録
reg add "HKLM\SOFTWARE\Classes\*\shell\VSCode\command" /ve /d "\"C:\Program Files\Microsoft VS Code\Code.exe\" --extensions-dir \"C:\ProgramData\vscode-extensions\" \"%1\"" /f
reg add "HKLM\SOFTWARE\Classes\Directory\shell\VSCode\command" /ve /d "\"C:\Program Files\Microsoft VS Code\Code.exe\" --extensions-dir \"C:\ProgramData\vscode-extensions\" \"%1\"" /f
reg add "HKLM\SOFTWARE\Classes\Directory\Background\shell\VSCode\command" /ve /d "\"C:\Program Files\Microsoft VS Code\Code.exe\" --extensions-dir \"C:\ProgramData\vscode-extensions\" \"%V\"" /f

REM --extensions-dir 付きで起動する code.cmd ラッパを作成
REM （%* を echo で書くと対話的 cmd で失われるため、PowerShell で [char]37+'*' を書き出す）
powershell -NoProfile -Command "$pct=[char]37; $q=[char]34; $c='@echo off'+[char]13+[char]10+$q+'C:\Program Files\Microsoft VS Code\bin\code.cmd'+$q+' --extensions-dir '+$q+'C:\ProgramData\vscode-extensions'+$q+' '+$pct+'*'+[char]13+[char]10; [IO.File]::WriteAllText('C:\ProgramData\vscode-extensions\vscode.cmd',$c,[Text.Encoding]::ASCII)"

REM 拡張機能のインストール
set "CODE=C:\Program Files\Microsoft VS Code\bin\code.cmd"
"%CODE%" --extensions-dir "C:\ProgramData\vscode-extensions" --uninstall-extension GitHub.copilot
"%CODE%" --extensions-dir "C:\ProgramData\vscode-extensions" --uninstall-extension GitHub.copilot-chat
"%CODE%" --extensions-dir "C:\ProgramData\vscode-extensions" --install-extension ms-python.python
"%CODE%" --extensions-dir "C:\ProgramData\vscode-extensions" --install-extension ms-python.vscode-pylance
"%CODE%" --extensions-dir "C:\ProgramData\vscode-extensions" --install-extension ms-python.debugpy
"%CODE%" --extensions-dir "C:\ProgramData\vscode-extensions" --install-extension MS-CEINTL.vscode-language-pack-ja
"%CODE%" --extensions-dir "C:\ProgramData\vscode-extensions" --install-extension saoudrizwan.claude-dev
"%CODE%" --extensions-dir "C:\ProgramData\vscode-extensions" --install-extension rust-lang.rust-analyzer
"%CODE%" --extensions-dir "C:\ProgramData\vscode-extensions" --install-extension tamasfe.even-better-toml
"%CODE%" --extensions-dir "C:\ProgramData\vscode-extensions" --install-extension anthropic.claude-code
"%CODE%" --extensions-dir "C:\ProgramData\vscode-extensions" --install-extension almenon.arepl
"%CODE%" --extensions-dir "C:\ProgramData\vscode-extensions" --list-extensions --show-versions

REM settings.json を作成（自動更新オフ、Python、Claude Code 設定）
if not exist "%APPDATA%\Code\User" mkdir "%APPDATA%\Code\User"
python -c "import json,os;data={'update.mode':'none','update.enableWindowsBackgroundUpdates':False,'extensions.autoUpdate':False,'python.defaultInterpreterPath':r'C:\Program Files\Python312\python.exe','claudeCode.environmentVariables':[{'name':'ANTHROPIC_API_KEY','value':'not-needed'},{'name':'ANTHROPIC_AUTH_TOKEN','value':'ollama'},{'name':'ANTHROPIC_BASE_URL','value':'http://localhost:11434'},{'name':'ANTHROPIC_MODEL','value':'glm-4.7-flash'},{'name':'CLAUDE_CODE_DISABLE_NONESSENTIAL_TRAFFIC','value':'1'}]};p=os.path.join(os.environ['APPDATA'],'Code','User','settings.json');open(p,'w',encoding='utf-8').write(json.dumps(data,indent=4));print('Done:',p)"

REM 自動更新の抑止ポリシー（settings.json に加えて、レジストリ側でも明示的にオフ）
reg add "HKLM\SOFTWARE\Policies\Microsoft\VSCode" /v "UpdateMode" /t REG_SZ /d "none" /f
echo === セットアップ完了 ===

2. Python インタプリタの選択

同一マシンに複数の Python がインストールされている場合，VS Code で使用する Python 本体（インタプリタ：Python プログラムを解釈・実行するソフトウェア）を選択する必要がある．

コマンドパレット（コマンド名で機能を呼び出す VS Code の入力欄）を開く（Ctrl+Shift+P）
Python: Select Interpreter と入力する
表示される一覧から，使用する Python（例：C:\Program Files\Python312\python.exe）を選択する．

Python プログラム実行手順

[Windows での Python プログラム実行手順を見るには、ここをクリック]

Windows での Python 実行手順（Visual Studio Codeを使用）

プログラムファイルの作成と保存

左サイドバーの「エクスプローラー」アイコン（Ctrl+Shift+E）をクリックする
「NO FOLDER OPENED」（作業対象フォルダが未選択の状態）と表示される場合は，「Open Folder」をクリックし，プログラムを保存するフォルダを選択する

続いて「フォルダを信用するか」を確認する画面（フォルダ内のコードを実行してよいか確認する VS Code の仕組み）が表示されるので，チェックして Yes を選択する
フォルダ名の右側に表示される「新しいファイル」アイコンをクリックする
ファイル名（例：aitask.py．ファイル名は何でも良い）を入力し Enter を押す．拡張子は .py（Python ファイルを示す拡張子）とする
実行したいコードを選択し，Ctrl+C でコピーする．VS Code のエディタ領域に Ctrl+V で貼り付ける
Ctrl+S で保存する

プログラムの実行

エディタ右上の三角形「▷」アイコン（Run Python File：現在開いている Python ファイルを実行するボタン）をクリックする．または，エディタ上で右クリックし「ターミナルで Python ファイルを実行」を選択する
VS Code 下部のターミナル（コマンドの入出力を表示する画面）に，実行結果（print 関数の出力等）が表示される
tkinter（Python 標準の GUI ライブラリ）のファイル選択ダイアログを使うプログラムを実行した場合は，ダイアログが開くので対象画像を選択する
VS Code 下部のターミナルで実行結果を確認する．OpenCV ウィンドウ（OpenCV が画像を表示するために開く専用ウィンドウ）が開いた場合はそちらも確認する．OpenCV ウィンドウは，マウスクリックでウィンドウをアクティブ（操作対象の状態）にしてからキーを押すと終了する

2. 機械学習の概要とPyTorchによる実装例

機械学習は、訓練データを用いて学習し、分類や予測などの能力を獲得する技術である。訓練データは、学習に使用するデータである。学習の手順は以下のとおりである。

データの準備（目的に応じた訓練データを準備する）
学習の実行（データからパターンを学習し、モデルを構築する）
タスクの実行（新しいデータを処理する）

機械学習の特徴は以下のとおりである。

データを用いて性能を向上させる
データのパターンを自動で抽出する
人手による規則の記述が不要である

応用事例には、画像認識、自然言語処理、予測などがある。

MNISTデータセットは、手書き数字（0〜9）の画像データセットであり、機械学習の入門用に使用される。

訓練用60,000枚、テスト用10,000枚で構成される
各画像は28×28ピクセルのグレースケールである
各画像に正解ラベル（0〜9）が付与されている

次章の演習では、MNIST を用いて手書き数字を分類するニューラルネットワークを学習・評価するプログラムを実行する。GPU がある環境では GPU を、ない環境では CPU を使用する。

プログラムで用いる用語を以下に示す（詳しい仕組みは第4章以降で説明する）。

バッチ：訓練データを少数ずつまとめた単位（演習のプログラムでは1バッチ64枚）。1枚ずつではなくまとめて処理することで学習が効率化される
エポック：訓練データ全体を1巡すること（演習のプログラムでは5エポック繰り返す）
データローダー（DataLoader）：データセットをバッチに分割し、順に供給する仕組み
損失関数：出力と正解のずれを1つの数値で表す関数（ここでは分類向けの交差エントロピー CrossEntropyLoss を用いる）

出力層に活性化関数を適用しない理由：演習のモデルでは、中間層には ReLU を適用するが、出力層には活性化関数を適用せず、生の出力値（ロジット）をそのまま返す。これは、CrossEntropyLoss が内部で Softmax 相当の処理（出力を確率に変換する処理）を含むため、出力層で別途 Softmax を適用する必要がないからである。第6章の「最も高い活性度を示すニューロンに対応するクラスが分類結果となる」という考え方はここでも適用され、評価時には torch.max によって最大の出力値を持つニューロンの番号を予測クラスとしている。

学習率0.1は、学習の進み方を調整する設定値の例である。値が大きすぎると学習が不安定になり、小さすぎると収束が遅くなる。

3. 演習1．MNISTの学習と正解率の確認

テーマ：MNIST データセットを用いた手書き数字分類モデルの学習と評価

手順

下記のプログラムを実行する（メモ帳を用いる場合は a.py のようなファイル名で保存して実行）。
エポックごとに表示される訓練損失と、最後に表示されるテストデータの正解率を記録する。
epochs の値を5から10に変更し、再度実行して結果を記録する。

ヒント：epochs は学習の実行部分で定義されている。CPU環境では実行に数分かかることがある。

考察ポイント：エポック数を増やすと訓練損失とテスト正解率がどのように変化するか。損失の減少と正解率の向上が対応しているかを確認する。

import torch
from torch import nn, optim
from torchvision import datasets, transforms

# デバイスの設定（GPUが使えればGPU、なければCPU）
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# データセットの準備（MNIST）
# ToTensor()によりピクセル値は0〜1に正規化される
transform = transforms.Compose([transforms.ToTensor()])
train_data = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
test_data = datasets.MNIST(root='./data', train=False, download=True, transform=transform)

# データローダーの設定(データをバッチに分割して供給する)
# batch_size=64: 1バッチ64枚  shuffle=True: 訓練時は順序をランダム化
train_loader = torch.utils.data.DataLoader(train_data, batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=64, shuffle=False)

class SimpleNN(nn.Module):
    def __init__(self):
        super().__init__()
        # 入力層784(=28×28)→中間層128→中間層64→出力層10(=クラス数0〜9)
        # 中間層のニューロン数128・64は設計者が選ぶ値（ハイパーパラメータ）である
        self.fc1 = nn.Linear(28*28, 128)
        self.fc2 = nn.Linear(128, 64)
        self.fc3 = nn.Linear(64, 10)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = torch.relu(self.fc2(x))
        # 出力層には活性化関数を適用しない(理由は本資料の第2章を参照)
        x = self.fc3(x)
        return x

# モデルをデバイスに移動
model = SimpleNN().to(device)
criterion = nn.CrossEntropyLoss()  # 分類向けの損失関数
optimizer = optim.SGD(model.parameters(), lr=0.1)  # 勾配降下法(学習率0.1)

# 学習の実行
epochs = 5
for epoch in range(epochs):
    model.train()  # 訓練モード(ドロップアウト等を訓練用に切り替える)
    running_loss = 0.0
    for images, labels in train_loader:
        # 28×28の画像を784次元の1次元ベクトルに変換し、データをデバイスに移動
        images = images.view(images.shape[0], -1).to(device)
        labels = labels.to(device)

        optimizer.zero_grad()             # 勾配の初期化
        output = model(images)            # フォワードプロパゲーション
        loss = criterion(output, labels)  # 損失の計算
        loss.backward()                   # バックプロパゲーション(勾配計算)
        optimizer.step()                  # 重みとバイアスの更新

        running_loss += loss.item()

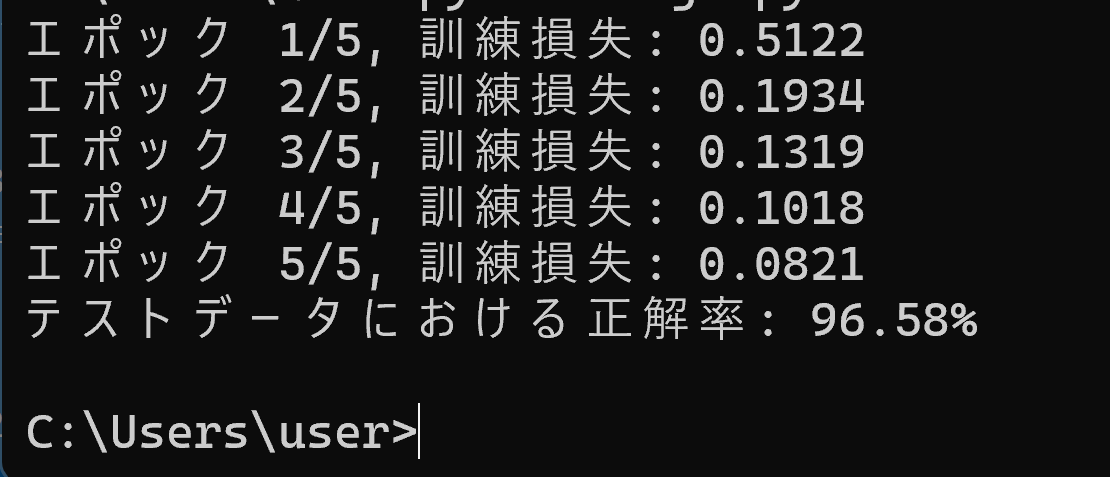
    print(f"エポック {epoch+1}/{epochs}, 訓練損失: {running_loss/len(train_loader):.4f}")

# モデルの評価
model.eval()  # 評価モード(ドロップアウト等を評価用に切り替える)
correct = 0
total = 0
with torch.no_grad():  # 勾配計算を止めてメモリと計算を節約(評価時は更新しないため)
    for images, labels in test_loader:
        images = images.view(images.shape[0], -1).to(device)
        labels = labels.to(device)
        outputs = model(images)
        # 最も大きい出力値を持つニューロンの番号を予測クラスとする
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print(f"テストデータにおける正解率: {100 * correct / total:.2f}%")

4. ニューラルネットワークの基本構造と仕組み

ニューラルネットワークは、機械学習の手法の一つであり、ニューロンと呼ばれる処理単位から構成される。各ニューロンは複数の入力信号を受け取り、以下の処理を行う。

入力の重みづけ：各入力信号に重み係数を乗算する。重みは各入力の重要度を表し、学習により調整される
重み付き和とバイアスの加算：重みづけされた入力値の総和にバイアス値を加算する。バイアスはニューロンの発火しやすさを調整する
活性化関数の適用：加算結果に活性化関数を適用し、出力値を決定する

この出力は、次層のニューロンへの入力として伝播される。

以下に、単一ニューロンの順伝播計算のプログラム例を示す。

# 単一ニューロンの順伝播計算
# 入力、重み、バイアスから出力値を計算する

inputs = [0.3, -0.5, 0.2]   # 入力値
weights = [0.1, 0.8, -0.5]  # 重み
bias = 0.2                  # バイアス

# 重み付き和の計算（各入力に対応する重みを掛けて合計）
weighted_sum = 0
for i in range(len(inputs)):
    weighted_sum += inputs[i] * weights[i]

# バイアスを加算
weighted_sum += bias

# ReLU活性化関数による出力計算（0以下なら0、そうでなければそのまま出力）
output = max(0, weighted_sum)

print(f"{inputs} -> {output}")

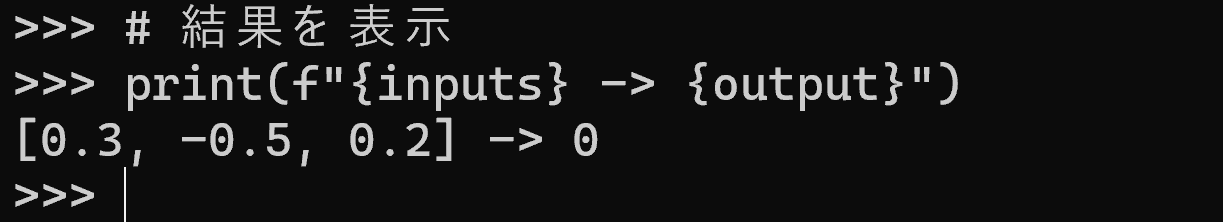
5. 活性化関数とその役割

活性化関数は、ニューロンの出力値を決定する関数であり、重み付き和とバイアスの加算結果に適用される。代表的な活性化関数として、ReLUとシグモイド関数がある。

ReLU（Rectified Linear Unit）は、以下の特徴を持つ。

入力が0未満の場合は0を出力する
入力が0以上の場合は、その値をそのまま出力する
ディープラーニングで使用される

シグモイド関数は、入力値を0から1の範囲の実数に変換する。

以下に、ReLUとシグモイド関数のプログラム例を示す。

import math

def relu(x):
    # ReLU活性化関数（0以下なら0、そうでなければそのまま出力）
    return max(0, x)

def sigmoid(x):
    # シグモイド活性化関数（入力を0〜1の範囲に変換）
    return 1 / (1 + math.exp(-x))

x1 = 1
x2 = -1
x3 = 0

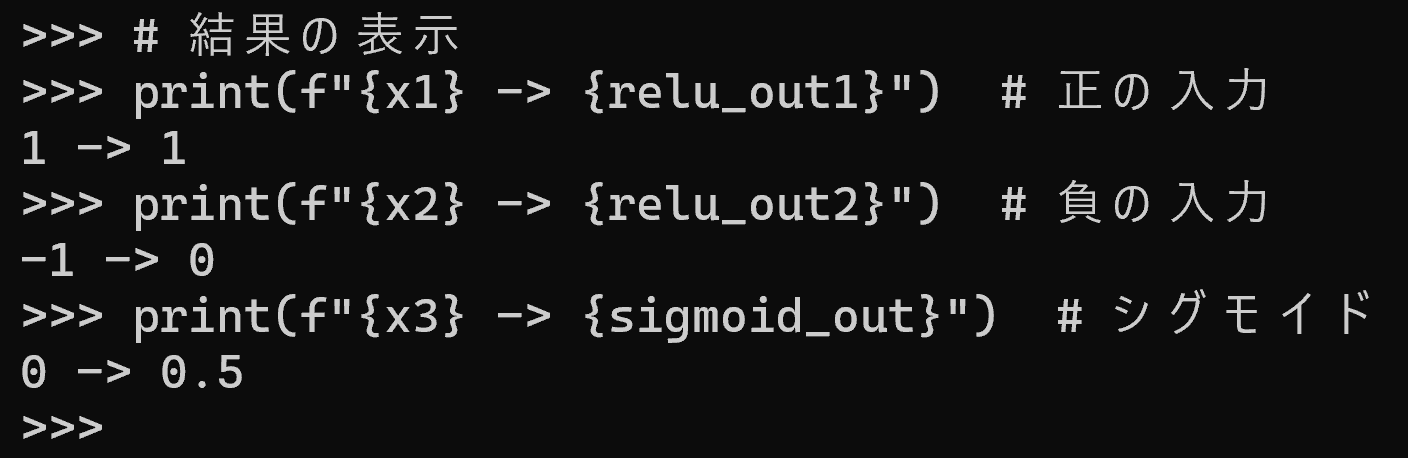
print(f"{x1} -> {relu(x1)}")     # ReLU（正の入力）
print(f"{x2} -> {relu(x2)}")     # ReLU（負の入力）
print(f"{x3} -> {sigmoid(x3)}")  # シグモイド

6. ニューラルネットワークの構造とフォワードプロパゲーション

ニューラルネットワークは、複数の層から構成される。各層は複数のニューロンで構成され、層間はニューロン同士の結合で接続される。入力層のニューロン数は入力データの大きさ（MNISTでは28×28＝784）に、出力層のニューロン数は分類するクラス数（MNISTでは0〜9の10）に対応する。中間層（隠れ層）のニューロン数は設計者が選ぶ値（ハイパーパラメータ）であり、タスクに応じて調整する。

フォワードプロパゲーションでは、入力データが入力層から出力層へと順方向に伝播する。各層のニューロンは、前層からの入力を処理し、その結果を次層へ伝達する。

分類タスクにおける出力層の構造は以下のとおりである。

出力層のニューロン数は、分類対象のクラス数に対応する
各出力ニューロンは活性度（実数値）を出力する
最も高い活性度を示すニューロンに対応するクラスが分類結果となる

以下のプログラムは、2入力3出力のニューラルネットワークによる3クラス分類を実装している。

# 2入力3出力のニューラルネットワークによる3クラス分類
# 入力層(2ニューロン)から出力層(3ニューロン)への順伝播計算を行う

inputs = [0.2, 0.8]  # 入力値

# 入力層から出力層への重み係数(2×3)
layer_weights = [
    [0.1, 0.4, 0.7],  # 入力1からの重み
    [0.2, 0.5, 0.8]   # 入力2からの重み
]

layer_bias = [0.1, 0.1, 0.1]  # 出力層の各ニューロンのバイアス

# 出力層の各ニューロンの出力を計算
output = [0] * 3
for j in range(3):  # 出力層の各ニューロンについて
    s = 0
    for i in range(2):  # 入力層の各ニューロンからの入力を合計
        s += inputs[i] * layer_weights[i][j]
    s += layer_bias[j]      # バイアスを加算
    output[j] = max(0, s)   # ReLU活性化関数

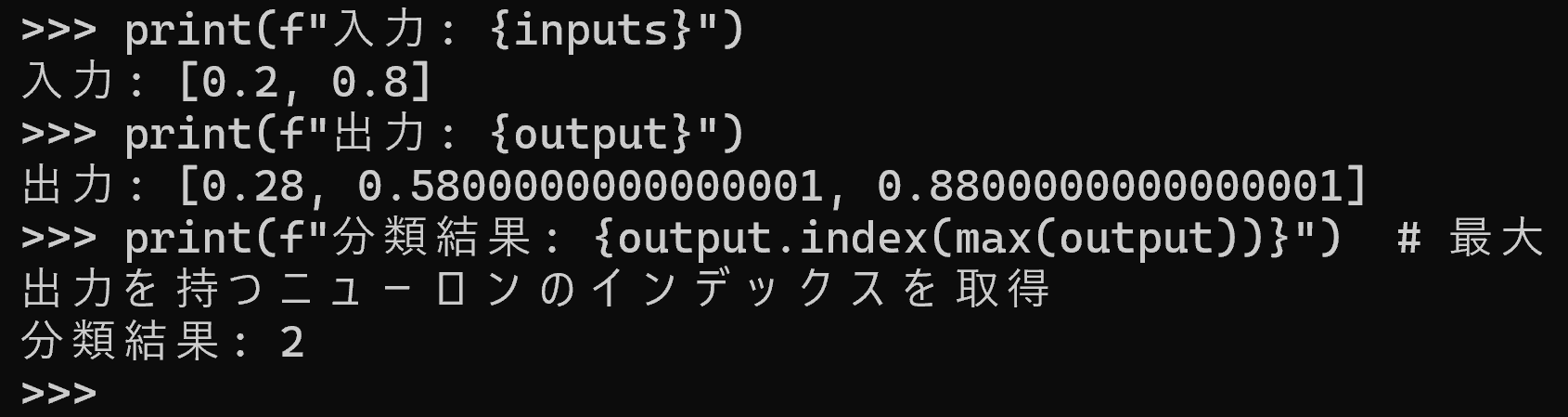
print(f"入力: {inputs}")
print(f"出力: {output}")
print(f"分類結果: {output.index(max(output))}")  # 最大出力を持つニューロンの番号

PyTorchによる実装

PyTorchを用いると、上記と同等の計算を簡潔に記述できる。

# 2入力3出力のニューラルネットワークによる3クラス分類（PyTorch版）
import torch

inputs = torch.tensor([0.2, 0.8])  # 入力データ（2ニューロン）

# 重み行列（入力2×出力3）
layer_weights = torch.tensor([
    [0.1, 0.4, 0.7],  # 入力1からの重み
    [0.2, 0.5, 0.8]   # 入力2からの重み
])

layer_bias = torch.tensor([0.1, 0.1, 0.1])  # 出力層の3ニューロン分のバイアス

# フォワードプロパゲーション
# 1. 入力と重みの行列積で重み付き和を計算
# 2. バイアスを加算
# 3. ReLU活性化関数を適用
output = torch.relu(torch.matmul(inputs, layer_weights) + layer_bias)

print(f"入力: {inputs.tolist()}")
print(f"出力: {output.tolist()}")
print(f"分類結果: {torch.argmax(output).item()}")  # 最大値を持つ番号

7. バックプロパゲーションと学習メカニズム

バックプロパゲーションは、ニューラルネットワークの学習アルゴリズムである。出力誤差を基に、出力層から入力層へと逆方向に誤差を伝播させ、各層の重みとバイアスを更新する。

学習の手順は以下のとおりである。

訓練データを用いてフォワードプロパゲーションを行い、出力を得る
出力と正解（教師信号）を損失関数で比較し、損失を計算する。損失関数は問題の種類により使い分け、第2章で扱ったような分類タスクでは交差エントロピーを、第8章の手計算例のような単純な数値合わせでは二乗誤差を用いる
損失の勾配を計算し、勾配降下法により重みとバイアスを更新する。勾配は、損失を小さくするために各重み・バイアスをどう変えればよいかを示す量である
訓練データを繰り返し使用し、損失を低減する

次章の演習では、二乗誤差を用いた重みの更新を、計算過程を明示した基本的な実装（プログラム1）と、PyTorchの自動微分機能を活用した実装（プログラム2）の2つの方法で示す。

8. 演習2．二乗誤差による重みの更新

テーマ：二乗誤差を損失関数とした重みとバイアスの更新（手計算実装と自動微分実装の比較）

手順

下記のプログラム1を実行し（メモ帳を用いる場合は a.py のようなファイル名で保存して実行）、誤差と更新後の重みを記録する。
同じ入力で下記のプログラム2を実行し、誤差と更新後の重みを記録する。
2つのプログラムの出力を比較する。

ヒント：両プログラムは同じ入力値、同じ初期重み、同じ学習率を用いている。プログラム1は更新式を明示的に記述し、プログラム2は自動微分で同じ計算を行う。

考察ポイント：手計算による更新（プログラム1）と自動微分による更新（プログラム2）で、更新後の重みが一致するかを確認する。

本演習では仕組みを理解しやすくするため、損失関数として二乗誤差を用いる。プログラム1は計算過程を明示した基本的な実装、プログラム2はPyTorchの自動微分機能を活用した実装である。

プログラム1：基本的な実装

# 入力層(2)→出力層(3)のニューラルネットワークの学習
# ReLU活性化関数を使用し、二乗誤差により重みとバイアスを更新する

inputs = [0.2, 0.8]
target = [1, 0, 0]  # 正解ラベル（3クラス分類の1番目）
learning_rate = 0.1

# 初期重みとバイアス
layer_weights = [
    [0.1, 0.4, 0.7],  # 入力1からの重み
    [0.2, 0.5, 0.8]   # 入力2からの重み
]
layer_bias = [0.1, 0.1, 0.1]  # 出力層の各ニューロンのバイアス

# フォワードプロパゲーション
output = [0, 0, 0]
for j in range(3):
    s = 0
    for i in range(2):
        s += inputs[i] * layer_weights[i][j]
    s += layer_bias[j]
    output[j] = max(0, s)   # ReLU活性化関数

# 誤差の計算（教師信号と出力の差）
errors = [target[j] - output[j] for j in range(3)]

# 勾配降下法による重みとバイアスの更新
# 二乗誤差 L = Σ(target - output)^2 の勾配は -2(target - output)*入力 となるため、
# 更新式の係数に 2 が現れる
for j in range(3):
    if output[j] > 0:  # ReLUの勾配は出力が正のときのみ1
        for i in range(2):
            layer_weights[i][j] += 2 * learning_rate * errors[j] * inputs[i]
        layer_bias[j] += 2 * learning_rate * errors[j]

print(f"誤差: {errors}")
print(f"更新後の重み: {layer_weights}")

プログラム2：PyTorchによる実装

PyTorchの自動微分機能では、勾配を手計算せずに求められる。requires_grad=True を指定したテンソルに対して行った計算は記録され、loss.backward() を呼ぶと各テンソルの勾配が .grad に格納される。勾配は backward() を呼ぶたびに加算されるため、更新後に zero_() でゼロに戻し、次回の計算に前回の勾配が混ざらないようにする。

# 入力層(2)→出力層(3)のニューラルネットワークの学習（PyTorch版）
import torch

inputs = torch.tensor([0.2, 0.8])
target = torch.tensor([1.0, 0.0, 0.0])  # 正解ラベル（3クラス分類の1番目）
learning_rate = 0.1

# 重みとバイアスの初期化（requires_gradを設定して勾配計算を有効化）
layer_weights = torch.tensor([
    [0.1, 0.4, 0.7],
    [0.2, 0.5, 0.8]
], requires_grad=True)
layer_bias = torch.tensor([0.1, 0.1, 0.1], requires_grad=True)

# フォワードプロパゲーション
output = torch.relu(torch.matmul(inputs, layer_weights) + layer_bias)

# 二乗誤差による損失の計算（出力と正解のずれの二乗の総和）
loss = torch.sum((target - output) ** 2)

# 更新前に誤差を記録（detach()で勾配計算の対象から外す）
errors = (target - output).detach().tolist()

# バックプロパゲーション（各テンソルの.gradに勾配が格納される）
loss.backward()

# 勾配降下法による重みとバイアスの更新（更新操作は勾配計算の対象外にする）
with torch.no_grad():
    layer_weights -= learning_rate * layer_weights.grad
    layer_bias -= learning_rate * layer_bias.grad

    # 次回の計算に前回の勾配が加算されないよう、勾配をクリア
    layer_weights.grad.zero_()
    layer_bias.grad.zero_()

print(f"誤差: {errors}")
print(f"更新後の重み: {layer_weights.tolist()}")

9. 過学習の概念と対策

過学習は、訓練データへの過剰な適合により発生する現象である。訓練データに含まれるノイズや偶発的なパターンまで学習し、未知のデータに対する性能が低下する。訓練データが少ない場合や、モデルのパラメータ数が多い場合に発生しやすい。

対策は以下のとおりである。

訓練データの増加
モデルの複雑さの抑制（層数やニューロン数の調整）
検証データによる過学習の検出
ドロップアウト：学習時にランダムにニューロンを無効化する手法。第3章のコードで model.train() と model.eval() を切り替えていたのは、こうした学習時のみ有効な処理を、評価時には無効にするためである
正則化（L1、L2）：重みの大きさに制約を加える手法

10. ディープラーニングの概要

ディープラーニングは、多層のニューラルネットワークを使用する機械学習の手法である。「ディープ」という名称は、多層構造に由来する。

ディープラーニングは、画像認識、自然言語処理、音声認識などのタスクで使用される。これを支える要素には、活性化関数（ReLUなど）、ドロップアウトなどの正則化手法、大規模データ、高性能な計算機環境（GPUなど）がある。

11. まとめ

ニューラルネットワークは、ニューロンによる入力の重みづけ、重み付き和とバイアスの加算、活性化関数の適用を基本とする。フォワードプロパゲーションにより入力から出力へデータが伝播し、バックプロパゲーションにより重みとバイアスが更新される。学習では、出力と正解のずれを損失関数で数値化し、その勾配にもとづいて勾配降下法でパラメータを更新する。損失関数は問題の種類により使い分け、分類では交差エントロピーを、単純な数値合わせでは二乗誤差を用いる。訓練データを繰り返し使用することで損失を低減し、目的のタスクを実行できるようになる。