Python のまとめ(Google Colaboratoryを含む)
【要点】 このページは,Pythonの基礎から応用までの一連の知識と手続きについて詳述している.Pythonの起動やインストール方法についてWindowsとUbuntu の両方に対応して説明し,さらに複数バージョンの管理やパッケージ管理ツールpipの使い方も解説している.また,Pythonの隔離環境venvやAnaconda3,Google ColaboratoryといったPython環境の設定も詳しく記載している.さらに,Pythonプログラムの例として,グラフ描画や画像ファイルの操作,主成分分析やk-meansクラスタリングなどを紹介.そして,Python開発環境として,Jupyter Notebook,Jupyter Lab,Nteract,spyderなどのインストール方法と起動方法を解説.最後にPythonのプログラミング基礎,データ型,モジュールとライブラリ,クラス定義とオブジェクト生成,制御構造,関数定義等についても触れている.
【目次】
- Python プログラムの実行
- Python のインストール
- Google Colaboratory
Google Colaboratory はオンラインの Python 開発環境
- Google Colaboratory の主な機能
- Google Colaboratory で PYTHON 3 の新しいノートブックを新規作成
- Google Colaboratory でファイルのアップロードとダウンロード
- Google Colaboratory で TensorFlow,Keras のバージョン確認
- Google Colaboratory で NVIDIA CUDA のバージョン確認
- Google Colaboratory で GPU の確認
- Google Colaboratory を使用中であるかを判別する Python プログラム
- Google Colaboratory での画像表示
- Python プログラムの例と Google Colaboratory での実行結果
- Python 関係のツール
- pip
- Python パッケージ・インデックス (PyPI)
- Google Colaboratory での pip の操作
- Windows での pip の操作
- Ubuntu での pip の操作
- pip と setuptools を最新版に更新
- pip のインストールを手動で行いたい場合
- Python の setup.py の実行
- Python の build_ext の実行
- 「Geospatial library wheels for Python on Windows」のページ
- 2to3
- Python 開発環境,Python コンソール(Jupyter ノートブック (Jupyter Notebook),Jupyter Lab,Nteract,spyder)
- Python,pip,Python 開発環境,Python コンソールのコマンドでの起動
- Windows での Python 開発環境として,Jupyter Qt Console,Jupyter ノートブック (Jupyter Notebook),Jupyter Lab,Nteract,spyder のインストール
- Ubuntu での Python 開発環境として,Jupyter Qt Console,Jupyter ノートブック (Jupyter Notebook),Jupyter Lab,Nteract,spyder のインストール
- Python コンソール
- Jupyter Qt Console
- Jupyter ノートブック (Jupyter Notebook)
- Jupyter Lab
- Nteract
- spyder
- PyCharm
- Python プログラミングの基礎
- オブジェクトの生成と削除,同値,同一性
- 単純値のデータ型
- オブジェクトのタイプ(クラス名)の取得
- 文字列の演算子
- pandas データフレーム
- numpy 全般
- 1次元の配列
- 2次元の配列
- 2次元の配列の種々の処理
- numpy の npz 形式(numpy.ndarray)ファイルの書き出しと読み込み
- 2次元配列データのCSV ファイル読み書き
- メッシュグリッド
- 配列の次元を増やす
- リスト
- Pythonのモジュール
- Pythonのライブラリ
- Matplotlib を用いたプロット
- Matplotlib を用いた種々のプロット
- TensorFlow
- Keras
- 制御構造(条件分岐,繰り返し)
- 式と変数
- 関数定義,関数オブジェクト
- 式の抽象化と関数
- 式の評価のタイミング
- クラス定義,オブジェクト生成,属性アクセス
- メソッド
- スーパークラスからの継承
- ファイルの選択
- 画像ファイルの表示,画像ファイルの画像のサイズの取得
- ply ファイルの表示
【サイト内のPython関連主要ページ】
- Windows AI支援Python開発環境構築ガイド: 別ページ »で説明
- AIエディタ Windsurf の活用: 別ページ »で説明
- AIエディタCursorガイド: 別ページ »で説明
- Google Colaboratory: 別ページ »で説明
- Python(Google Colaboratoryを含む)のまとめ: 別ページ »で説明
- 機械学習の Python 実現ガイド: 別ページ »で説明
- 行列計算の Python 実現ガイド: 別ページ »で説明
- 統計分析のPython での実現ガイド: 別ページ »で説明
- 音声信号処理の Python 実現ガイド: 別ページ »で説明
- カラー画像処理の Python 実現ガイド: 別ページ »で説明
- Python 言語によるとても簡単なアドベンチャーゲーム(変数,式,if,while,関数,print,time.sleep, def, global を使用): 別ページ »で説明
- Pythonプログラミング講座:基礎から応用まで(授業資料,全15回): 別ページ »で説明
- Pythonプログラミングの例と実践ガイド: 別ページ »で説明
【外部リソース】
- Pythonの公式サイト: https://www.python.org
- 東京大学の「Pythonプログラミング入門」: https://utokyo-ipp.github.io/IPP_textbook.pdf
- ITmedia社の「Pythonチートシート」の記事: https://atmarkit.itmedia.co.jp/ait/articles/2004/20/news015.html
1. Pythonプログラムの実行
Pythonは人気の高いプログラミング言語の一つであり,読みやすく書きやすい文法と幅広い応用範囲を持つ.様々な分野で使用され,豊富なライブラリがある.1. (1) Google Colaboratoryによるオンライン実行
Google ColaboratoryはオンラインのPython開発環境である.詳しくは,このページの別項目で説明している.1. (2) WindowsでのPythonの起動
WindowsでのPythonのインストール: 別ページ »で説明
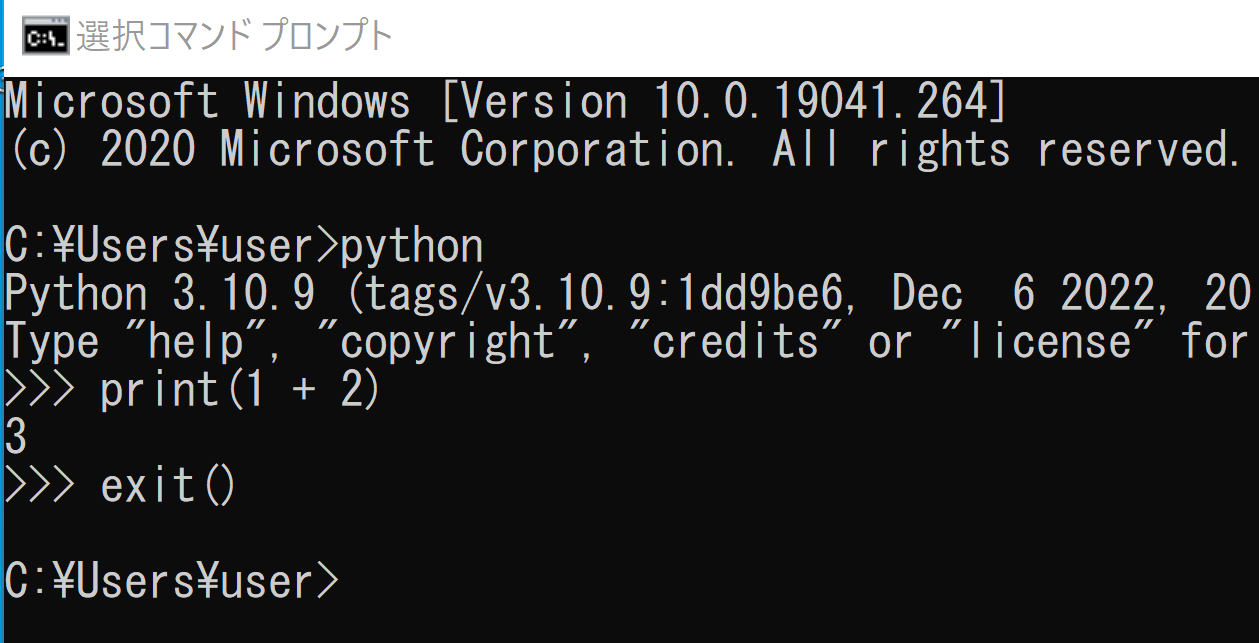
1. (3) UbuntuでのPythonの起動
UbuntuでPythonを起動する方法は以下のとおりである. システムPythonを使用 UbuntuのシステムPythonのPythonバージョン3は,「python3」で起動する. ```bash python3 ``` pyenvを用いてインストールしたPython pyenvを用いてインストールしたPythonは,pyenvの設定の後,「python」で起動する. venvを使用する場合 venvを使うときは,activateコマンドを実行した後,「python」で起動する.2. Pythonのインストール
2. (1) Python 3.12のインストール,pipとsetuptoolsの更新(Windows上)
Pythonの公式ページ: https://www.python.org/ Python開発環境,Pythonコンソール: 別項目で説明している.インストールでの注意点
インストール時には以下の点に注意する. Python 64ビット版の使用 Python 64ビット版を使用すること. システム領域へのインストール Pythonをシステム領域にインストールすることを推奨する.Windowsでは,Pythonをユーザ領域(既定の設定)またはシステム領域にインストールできる.ユーザー名に日本語が含まれている場合,Pythonをユーザ領域にインストールすると問題が発生する可能性がある.システム領域にインストールすることで,ファイルパスに日本語が含まれることを避けることができる. TensorFlow 2.10.1の利用 TensorFlow 2.10.1は次のPythonのバージョンと互換性がある: Python 3.10,Python 3.9,Python 3.8,Python 3.7 この互換性情報は,https://pypi.org/project/tensorflow/2.10/#filesで確認できる.TensorFlow 2.10.1は,Python 3.6以前のバージョン,Python 3.11以降のバージョンではサポートされていない(2024年7月時点).最新の互換性情報は公式ドキュメントで確認すること. 複数バージョンの同時インストール Windowsでは,Pythonの3.6.A,3.7.B,3.8.C,3.9.D,3.10.Eのように,複数のバージョンのPythonを同時にインストールできる.詳しくは,別項目で説明している.Python 3.10のインストール,pipとsetuptoolsの更新(Windows上)
WindowsでのPython 3.10のインストール手順は以下のとおりである. 1. TensorFlowのインストール予定がある場合には,次のページで必要なPythonのバージョンを確認する URL: https://pypi.org/project/tensorflow-gpu/#files 2. PythonのURLを開く URL: https://www.python.org 3. Windows版のPython 3.10をダウンロードする ページの上の方にある「Downloads」をクリックする.「Downloads」の下にメニューが出るので,その中の「Windows」をクリックする.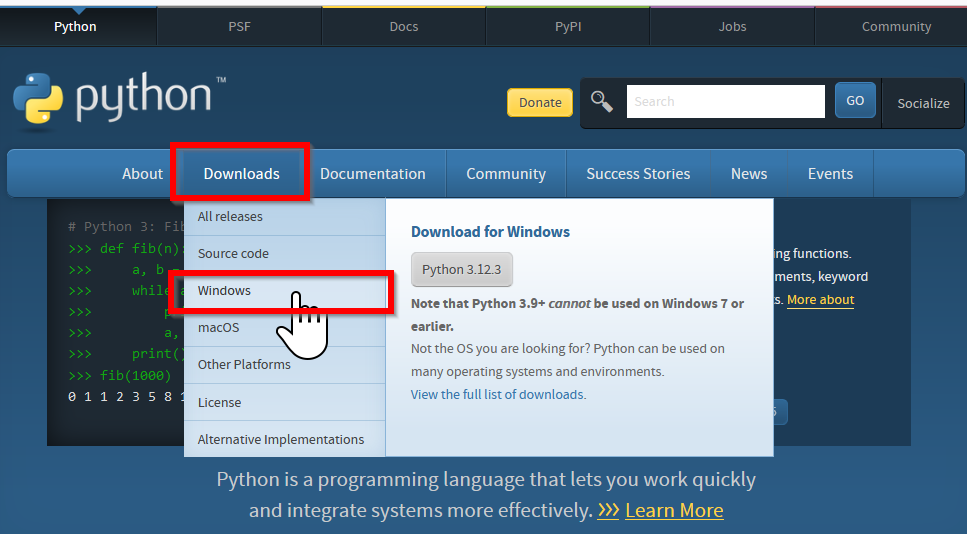
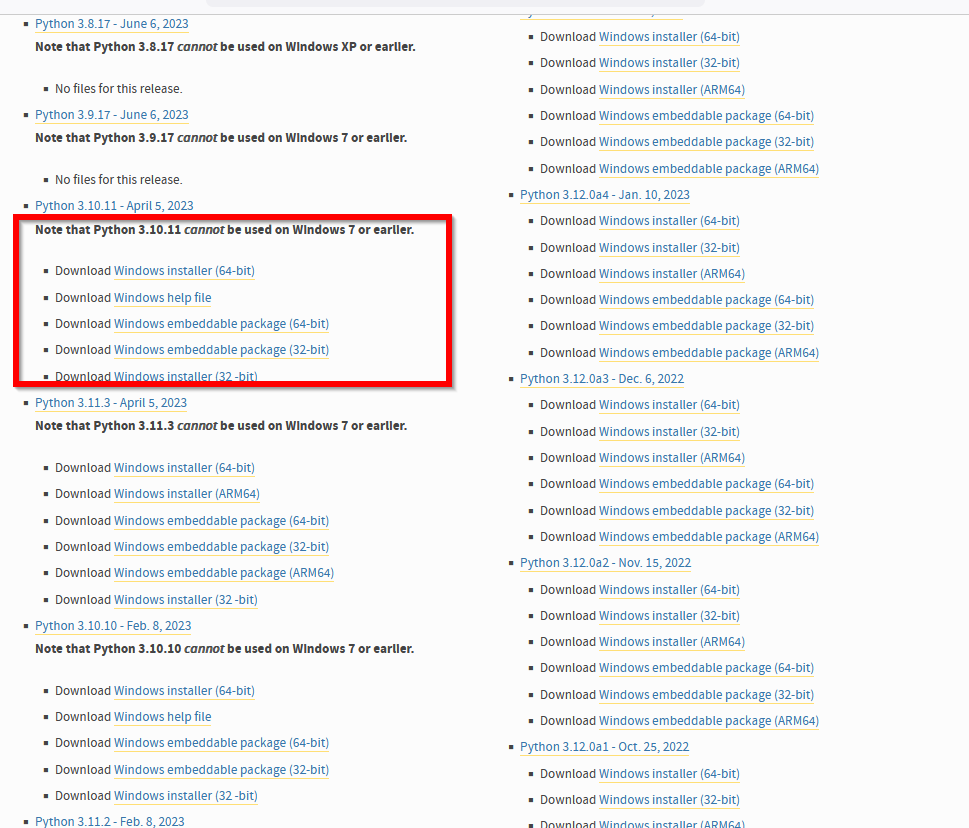
TensorFlowを使う予定がある場合は,https://pypi.org/project/tensorflow-gpu/#filesで必要なPythonのバージョンを確認しておく.2024年5月時点では,TensorFlowバージョン2.10が動くのは,Python 3.10またはPython 3.9またはPython 3.8またはPython 3.7である(https://pypi.org/project/tensorflow/2.10/#files)
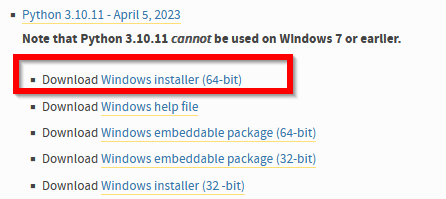

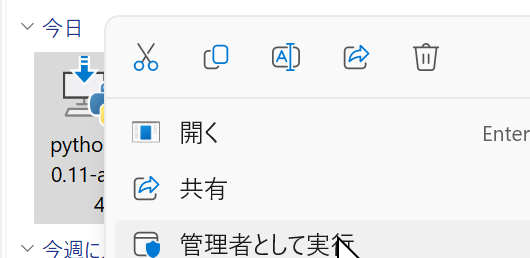
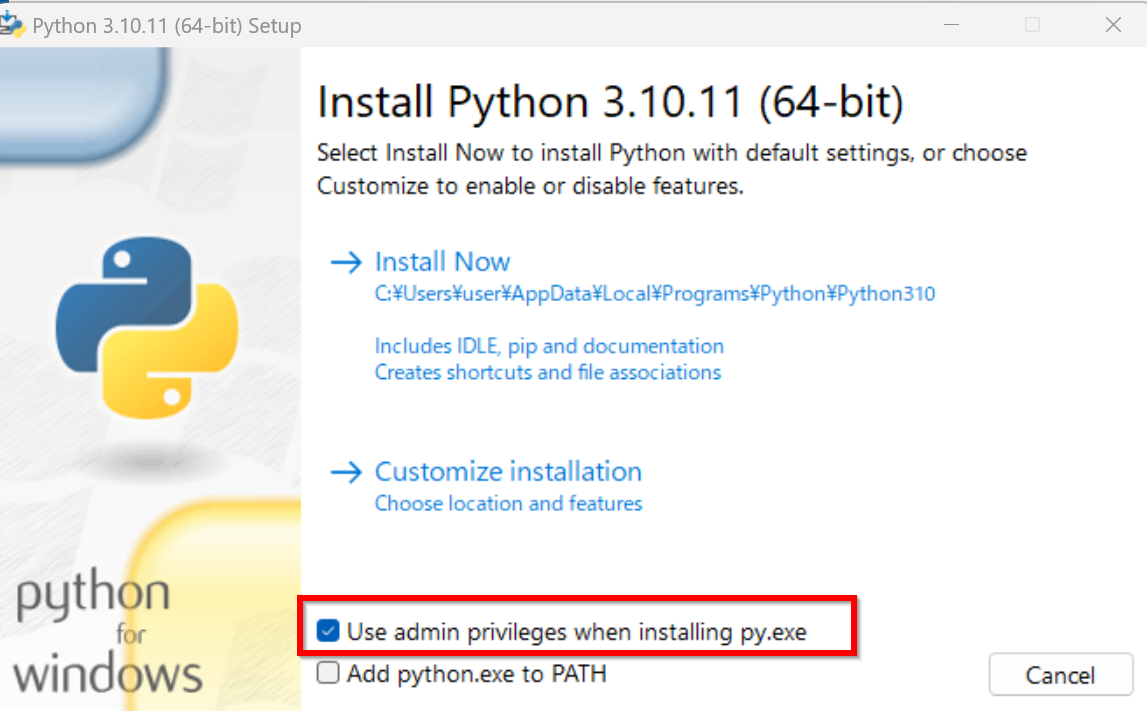
すでにPythonランチャーをインストール済みのときは,「Install launcher for all users (recommended)」がチェックできない場合がある.そのときは,チェックせずに進む
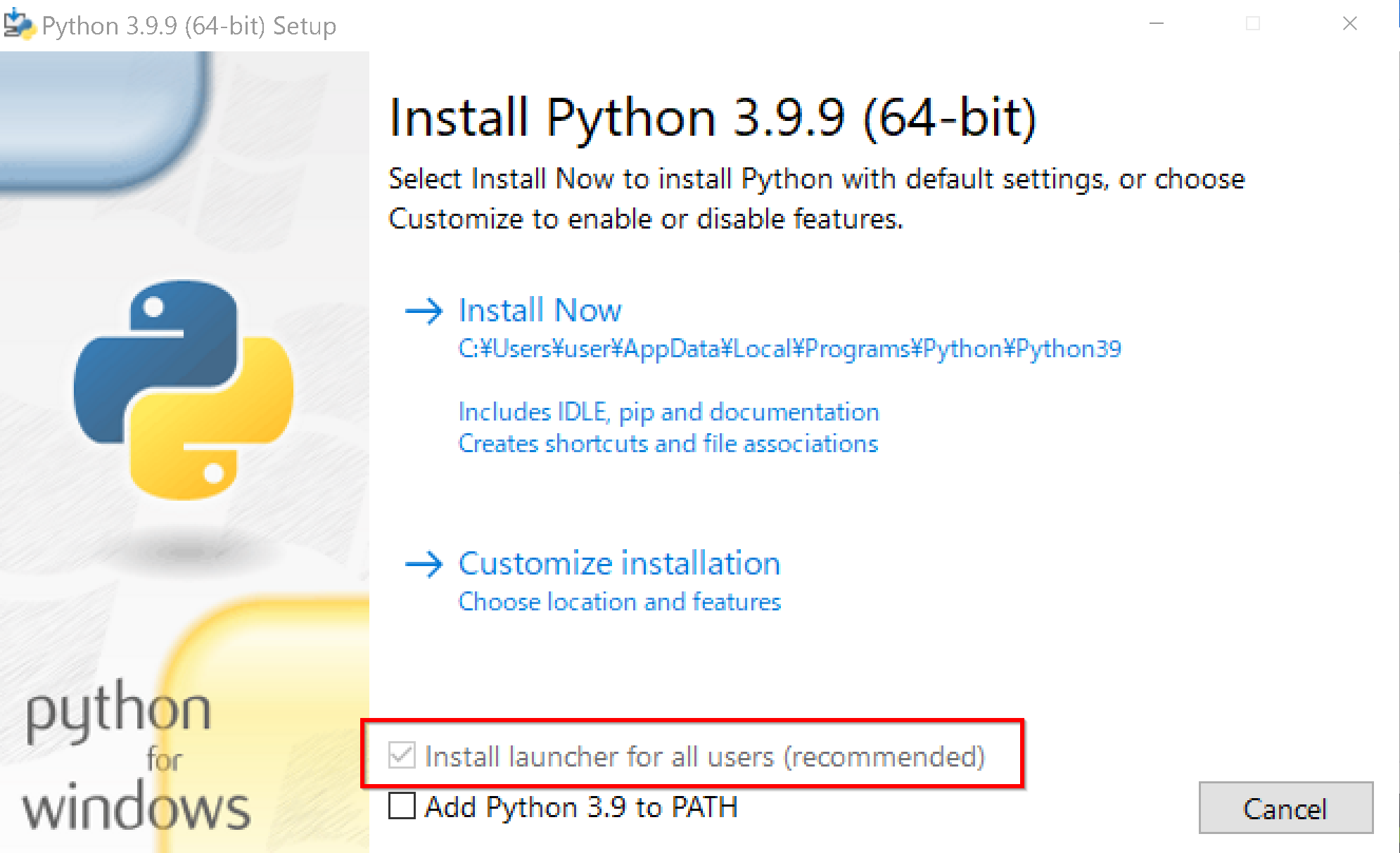
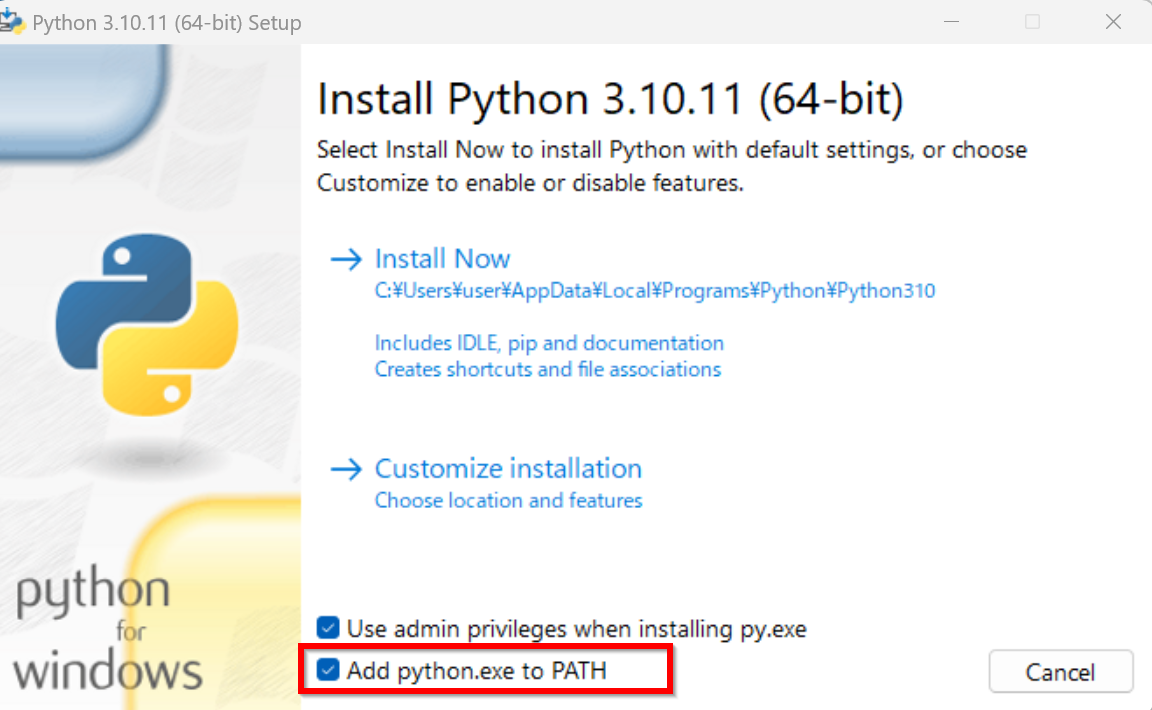
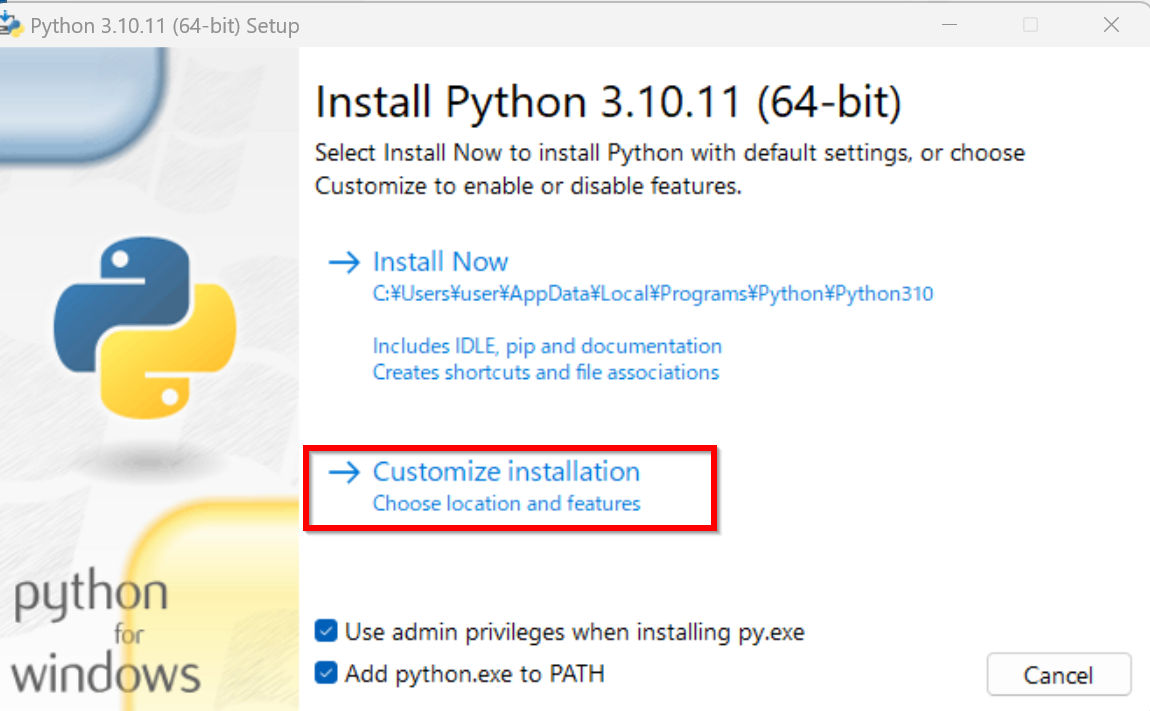
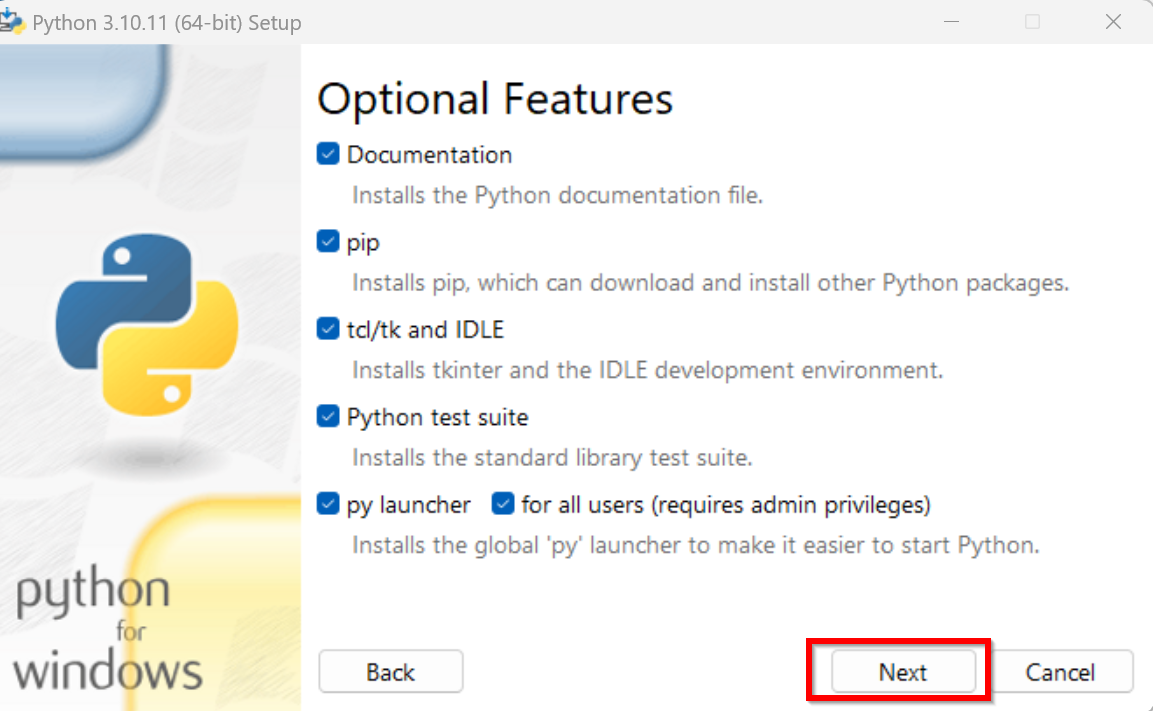
ユーザ名が日本語のときのトラブルを防ぐため
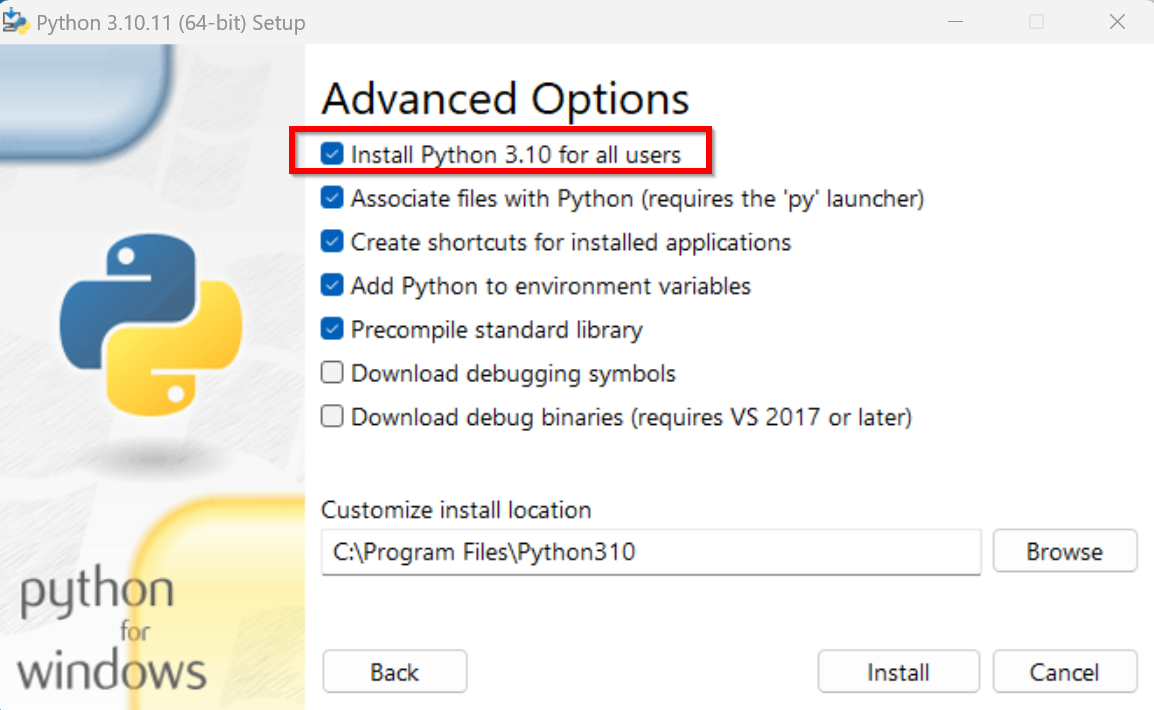
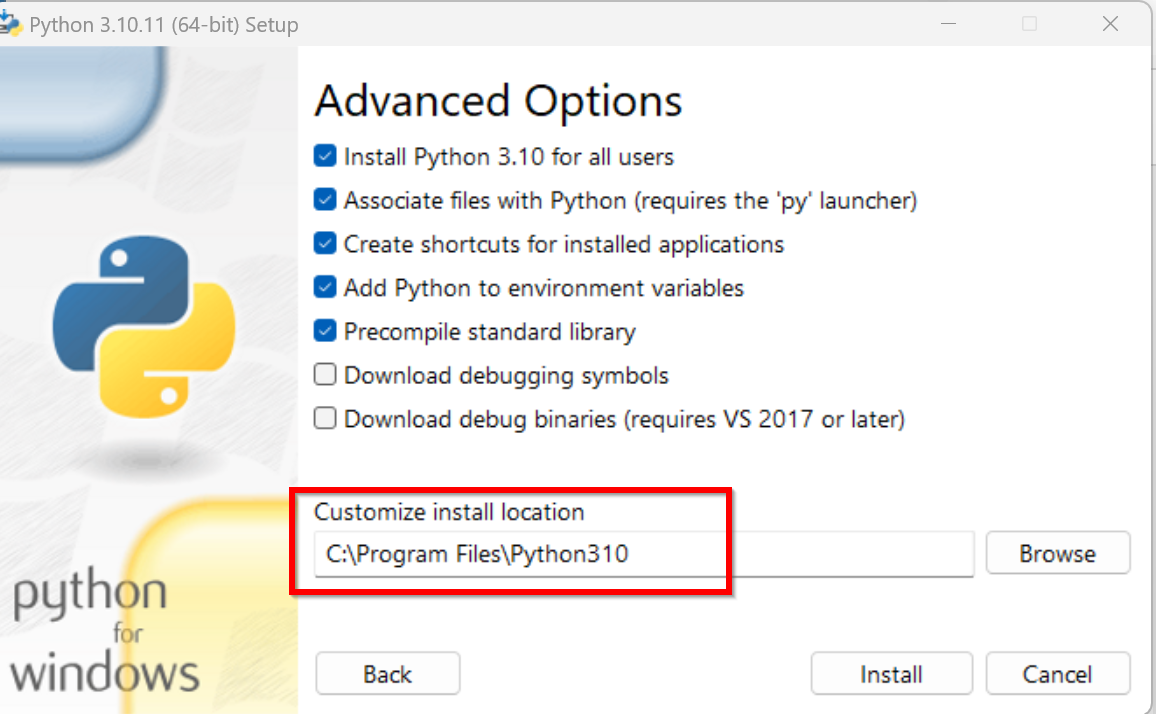
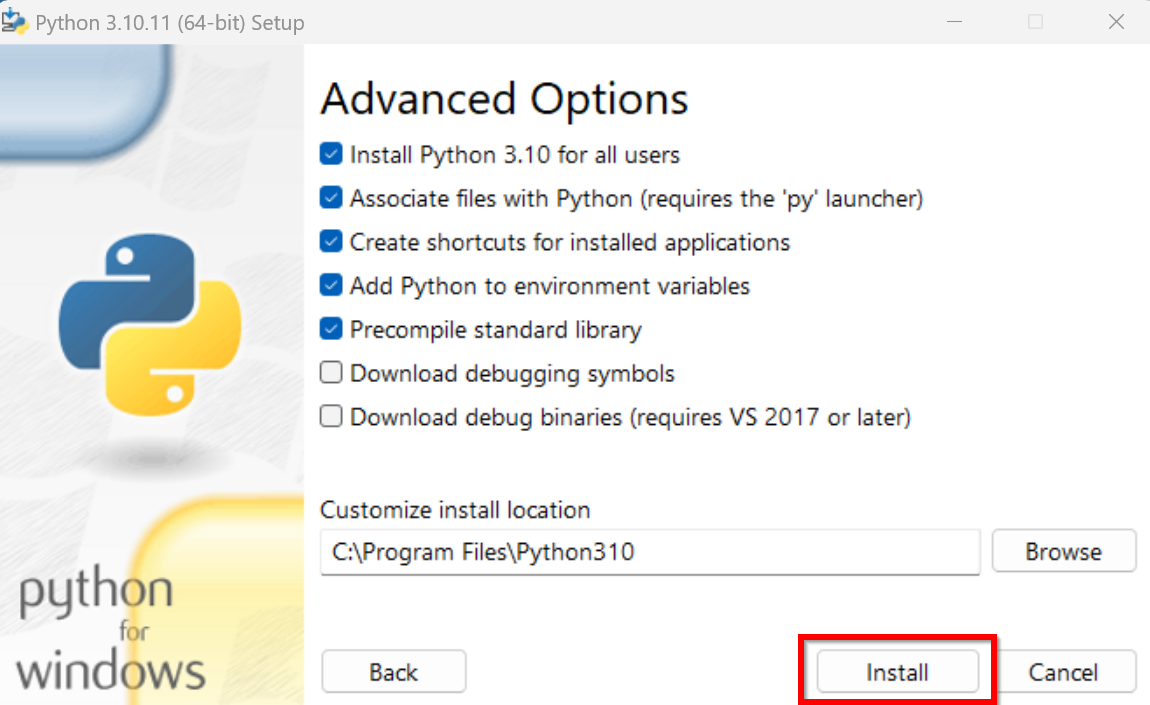
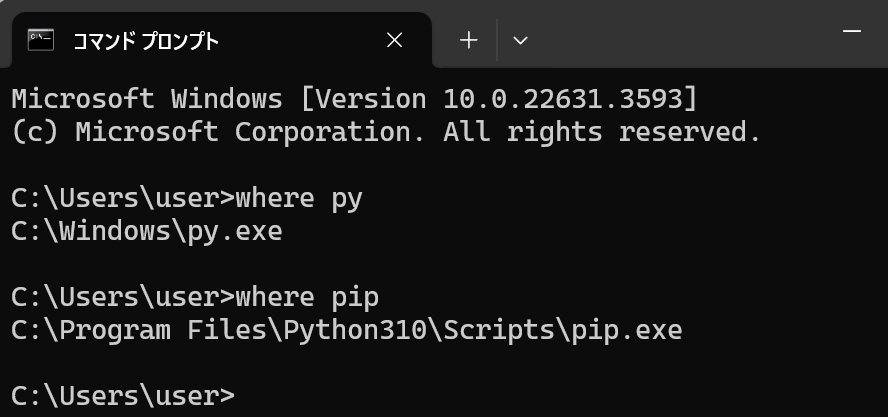
表示されないときは,システムの環境変数Pathに,C:\Program Files\Python310とC:\Program Files\Python310\Scriptsが追加済みであることを確認する(「310」のところは使用するPythonのバージョンに読み替えること).無ければ追加し,再度コマンドプロンプトを開いて,再度「where py」,「where pip」を実行して確認する
それでもうまく行かない場合は,Pythonのアンインストールを行う.過去のアンインストールが不完全だった可能性がある
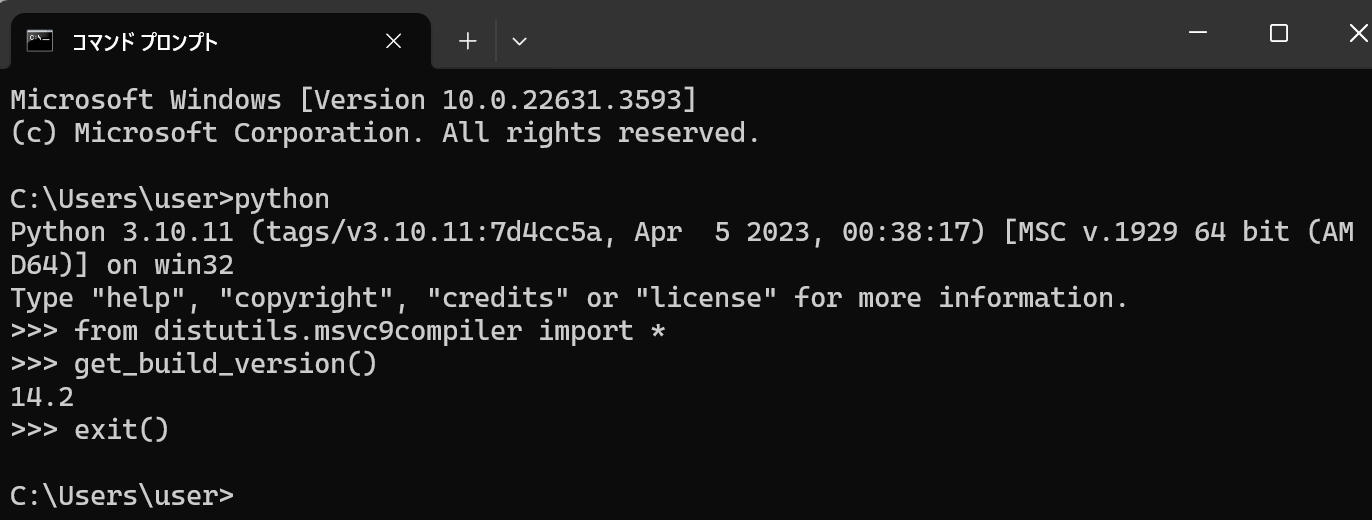
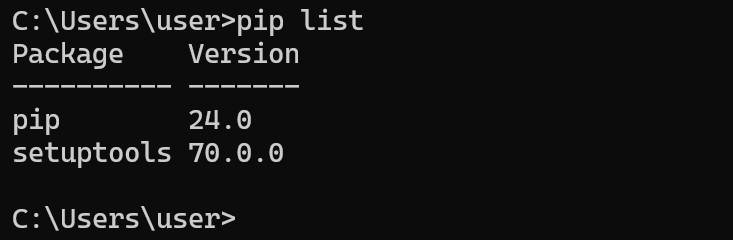
Pythonに関しての情報取得
Pythonにトラブルがあった時に役に立つ情報取得の手順をまとめている. 1. Windowsのシステム環境変数Pathを確認する インストール時に,「Add Python ... to PATH」をチェックしたので,Pythonについての設定が自動で行われる.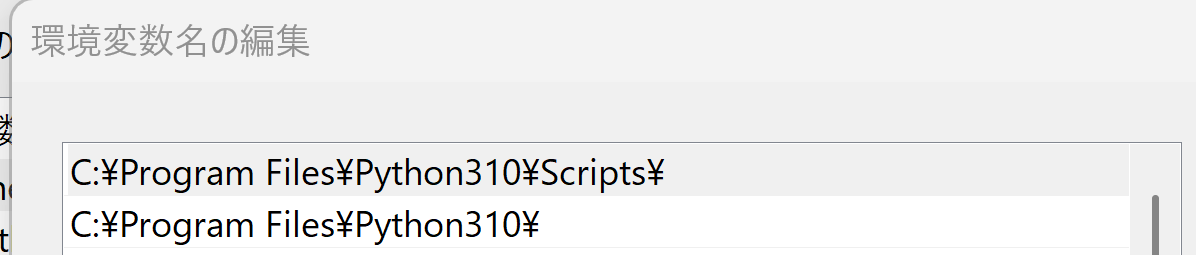
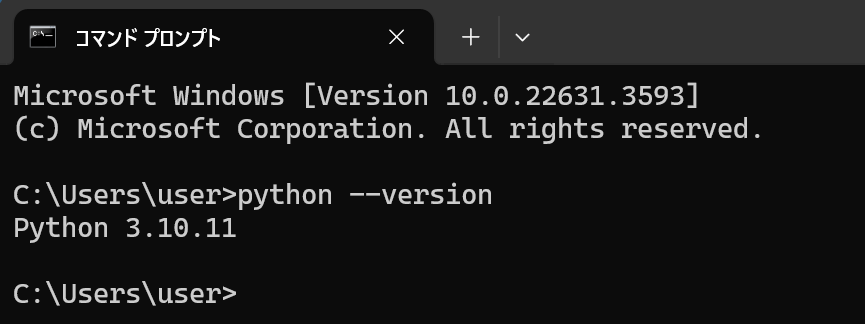
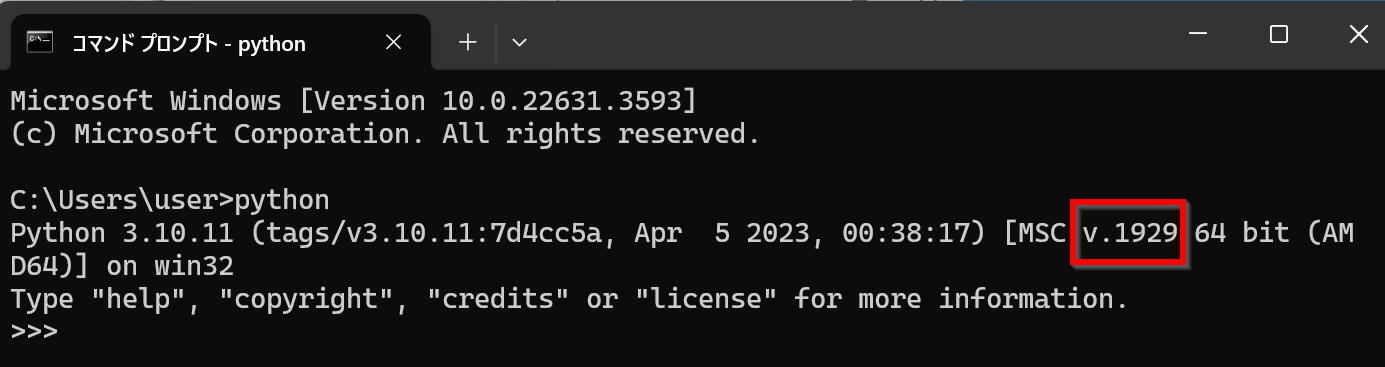
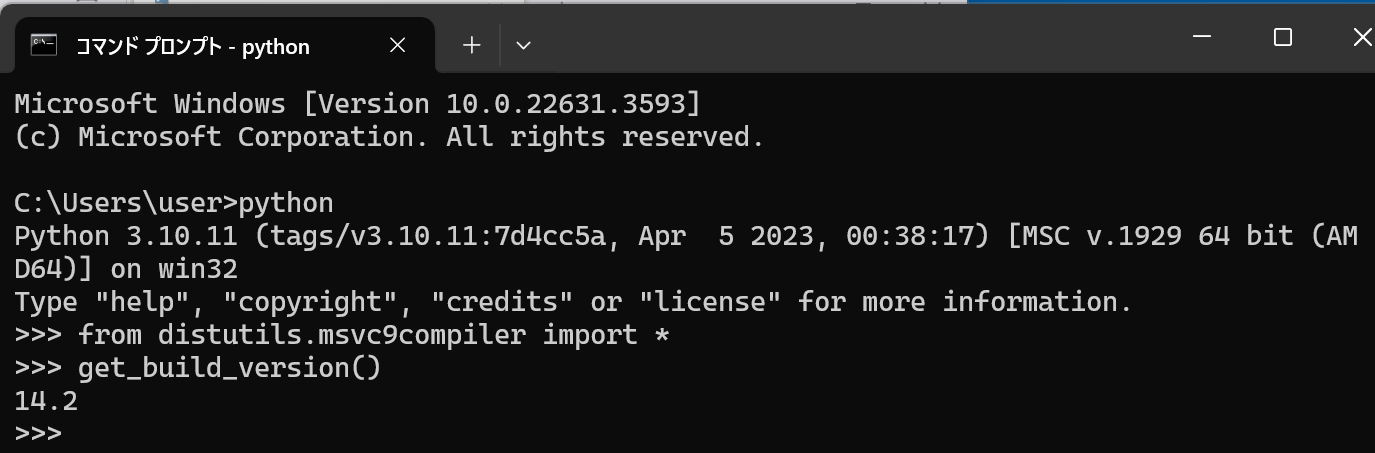
2. (2) WindowsでPythonのアンインストール
WindowsでPythonのアンインストールを行う手順は以下のとおりである. 1. まず,WindowsでPythonのアンインストール操作を行う 2. 次に,Python関係のファイルの削除を行う Windowsでは,コマンドプロンプトを管理者として実行し,次のコマンドを実行する. この操作は,必ずPythonをすべてアンインストールした後に行うこと.
次のコマンドは,rmdirを使用して,%APPDATA%\Pythonディレクトリを再帰的に削除する.次に,"C:\Program Files"ディレクトリに移動し,Python3で始まるディレクトリを検索し,見つかったディレクトリを再帰的に削除する
2. (3) Windowsでの複数のPythonの同時インストール
Windowsでは,Pythonの3.6.A,3.7.B,3.8.C,3.9.D,3.10.Eのように,複数のバージョンのPythonを同時にインストールできる. ただし,3.10.4と3.10.5の同時インストールはできない(3.Xのように,2桁目でバージョン番号が違うものを同時にインストールできる). そのときは,環境変数Pathの設定を常に意識すること.Pythonランチャーである「py」コマンドも利用すること. 複数のバージョンのPythonを同時にインストールしたとき,WindowsのPythonランチャーを用いて,インストールされているPythonのバージョンを調べたり,Pythonのバージョンを指定しての起動を行うことができる.Pythonのバージョンを指定してのpipやvenvの実行を行うときにも便利である.WindowsのPythonランチャーpy
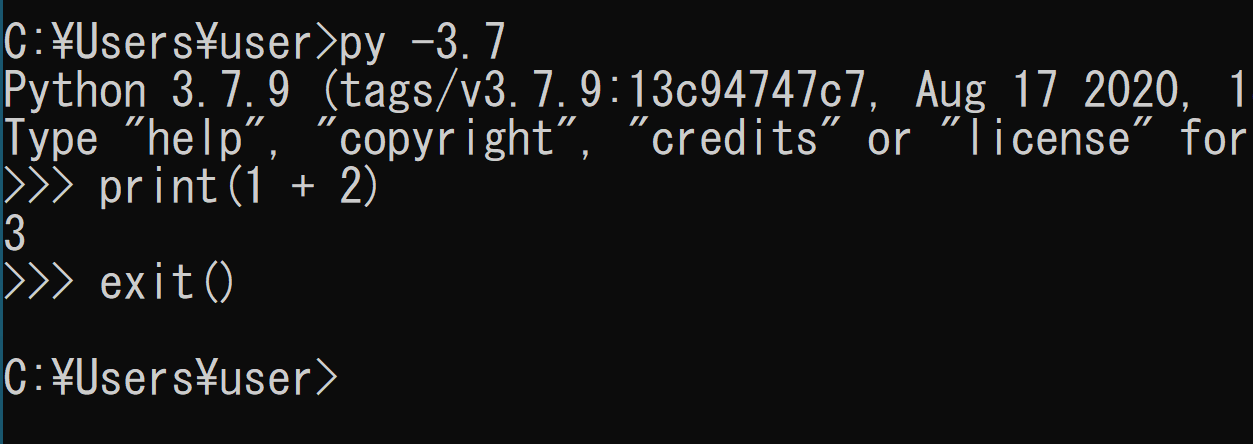
Pythonランチャーは,Windowsで動くツールである.複数バージョンのPythonを同時にインストールしたときに便利である. Pythonランチャーは,WindowsでのPythonのインストール時に,同時にインストールできる. Pythonの起動 Pythonランチャーを使わない場合,Pythonは,環境変数Pathで先頭のPythonが使用される. WindowsのPythonランチャーを用いて,次のように使用するPythonのバージョンを指定できる.「py」はWindowsのPythonランチャーのコマンドである. - py -3.10 - py -3.9 - py -3.8 - py -3.7 - py -3.6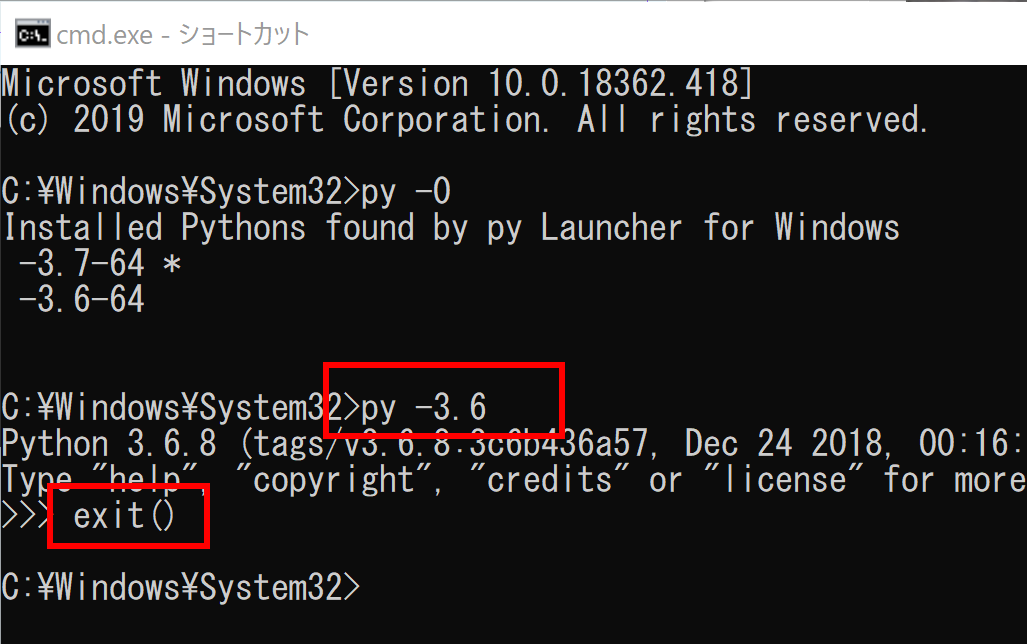
「py -X」のように,バージョン指定の中の「-32」,「-64」を省略することもできる.そのときは,PythonバージョンXが実行されるが,PythonのバージョンX 32ビット版と64ビット版をインストールしている場合は,64ビット版の方が実行される
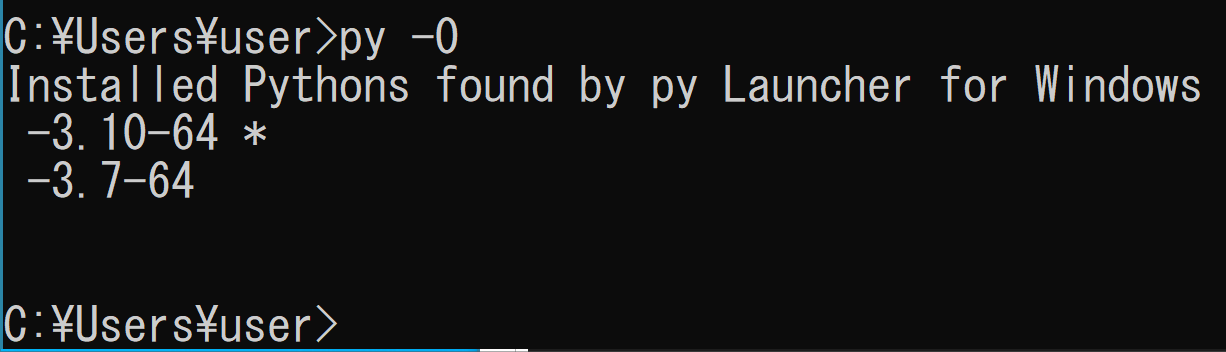
「py」のようにバージョン指定を省略したときは,インストールされているPythonの最新バージョンが実行される
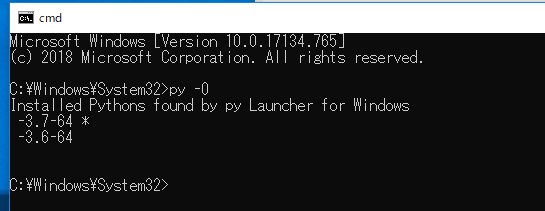
「-3.7-64」,「-3.8-32」,「-3.8-64」が表示されたとする.この場合,これら3つのバージョンがインストール済みであり,「py -3.7-64」や「py -3.8-32」や「py -3.8-64」でpythonを使うことができる
2. (4) UbuntuのシステムPython,UbuntuでのPythonのインストール,pipとsetuptoolsの更新
UbuntuのシステムPython
Ubuntuをインストールすると,UbuntuのシステムPythonも同時にインストールされる. Ubuntuの場合はシステムPythonを用いる(その場合はインストールは不要)か,pyenvなどを用いて,システムPythonとは隔離した形でインストールする. UbuntuでシステムPythonを使用するときは,改めてPythonのインストールを行う必要はない. UbuntuのシステムPythonを用いるとき,python,pipは,次のコマンドで起動できる. - python3(UbuntuのシステムPython) - sudo pip3(UbuntuのシステムPythonのpip) 「python3」や「pip3」のように「3」を付ける. 次の実行により,「python」や「pip」で,「3」を付けなくても済むようになる. ```bash sudo apt -y install python-is-python3 ```システムPythonを使っているときのpipとsetuptoolsの更新(Ubuntu上)
システムPythonを用いるときは,pip,setuptoolsの更新は次のコマンドで行う. ```bash sudo apt update sudo apt -y install python3-pip python3-setuptools ```UbuntuでのPythonのインストール(pyenvを使用)
Ubuntuで,システムPython以外のPythonをインストールするにはpyenvの利用が便利である.pyenvは,Linux,MacOSで動くPythonバージョン管理のツールである.Ubuntuをインストールすると,UbuntuのシステムPythonも同時にインストールされる.Ubuntuでは,システムPythonは,Ubuntuシステムの動作に関わっている.システムPythonをバージョンアップしたり,アンインストールを行ったりするのは良くない
pyenvについての詳細説明: 別ページ »で説明
2. (5) Pythonの隔離された環境
Pythonの隔離された環境
次のような場合は,Pythonの仮想環境が役に立つ.Pythonの仮想環境の利用には,Python 3.3以上で標準機能になったvenvが便利である.Python 3.3未満では,virtualenvが便利である.venvやvirtualenvの利用により,Pythonの隔離された環境を複数共存させることができる. 複数のPython環境の使用 複数のPython環境を使用するとき,あるPythonでのパッケージの変更や更新などが,他のPythonに影響しないように隔離する. UbuntuのシステムPythonとは別のPython環境 Ubuntuでは,Pythonの多くのパッケージはaptの管理下にある(例えば「sudo apt -y install python3-numpy」のようなコマンドでインストールする). 「pipでインストールするPythonのパッケージ」と「aptでインストールするPythonのパッケージ」が混在し,管理が難しくなったり,動作が不安定になる可能性がある. このような場合,UbuntuのPythonとは隔離された,別のPythonの環境を作ると便利である.Pythonの仮想環境では,すべてのパッケージをpipで管理するようにできる.venv
venvは,Pythonの仮想環境を作成する機能を提供するモジュールである.Pythonの仮想環境は隔離されており,特定のバージョンのPythonや,特定のバージョンやPythonパッケージを管理するのに役立つ. Pythonでは,さまざまなパッケージをインストールする.複数のバージョンのPythonを同時インストールすることもある.venvの利用により,次のメリットがある. - 簡単なコマンドで,「特定の1つのバージョンのPythonだけがインストールされたシステム」を仮想的に作ることができる - パッケージが違う複数のPython環境の共存使用法の要点を以下に示す
Pythonの隔離された環境の新規作成 既定(デフォルト)では,Pythonの隔離された環境に,システムのsite packageは含まれない. Windows: ```bash python -m venv <ディレクトリ名> ``` (環境変数Pathで先頭のPythonが使用される) ```bash pyWindowsで,Pythonの隔離された環境を扱う(venvを使用)
Windowsで,venvを用いて,新しいPythonの仮想環境の新規作成,有効化,無効化を行う. 1. 前もってPythonをインストールしておく.使用しているPythonのバージョンの確認は,次のコマンドで行うことができる ```bash python --version ``` 2. Pythonの仮想環境の作成と確認を行う ここでは,venvのためのディレクトリ名「%HOMEPATH%\.venv」を指定して,新しいPythonの仮想環境を生成する.「python -m venv」は,venvモジュールの実行である
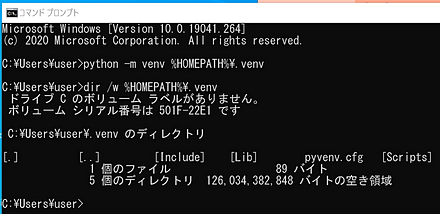

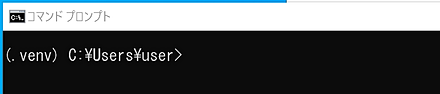
いま,venvを使用中かどうか,プロンプトの「(venv)」で分かる
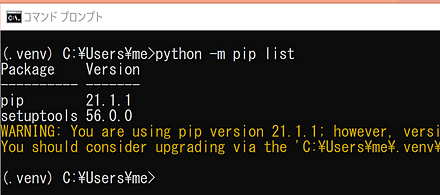

WindowsのPythonランチャーでバージョン指定して,Pythonの隔離された環境を扱う(venvを使用)
Windowsで,venvを用いて,新しいPythonの仮想環境の新規作成,有効化,無効化を行う. Pythonの仮想環境の新規作成では,Pythonランチャーを用いて,Pythonのバージョンを選ぶ. 1. Pythonランチャーで,インストール済みのPythonのバージョンを確認する ```bash py -0 ```このときの表示で,使いたいバージョンのPythonが無いときは,Pythonのインストールを行う
いま,venvを使用中かどうか,プロンプトの「(venv)」で分かる
UbuntuでPythonの隔離された環境を扱う(venvを使用)
venvを用いて,新しいPythonの仮想環境の新規作成,有効化,無効化を行う. 1. python3-venvのインストールを行う ```bash sudo apt update sudo apt -y install python3-venv ``` 2. 使用しているシステムPythonのバージョンの確認は,次のコマンドで行うことができる ```bash python3 --version ```
システムPythonと違うバージョンのPythonを使いたいときは,pyenvの利用が便利である.pyenvの詳細は,別ページ »で説明している
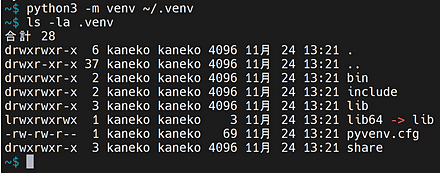

いま,venvを使用中かどうか,プロンプトの「(venv)」で分かる

virtualenv,virtualenv-wrapper
virtualenv,virtualenv-wrapperは,Pythonの仮想環境の作成ができるソフトウェアである.venvが対応していないようなPythonを使いたい場合には,virtualenv,virtualenv-wrapperが便利な場合がある. virtualenv-wrapperの使い方は次のとおりである. - mkvirtualenv2. (6) Pythonの種々のバージョン
Pythonの公式ページ: https://www.python.org/2. (7) Anaconda3
Anaconda3
Anaconda3は、Anaconda Inc.社が提供しているPythonバージョン3のソフトウェアである。言語処理系、開発ツール、パッケージ管理ツールconda、さまざまなPythonパッケージから構成されている。さらに、アプリケーションとしてSpyder、conda、Anaconda Prompt、Jupyter Notebook、Anaconda Navigatorが含まれている。
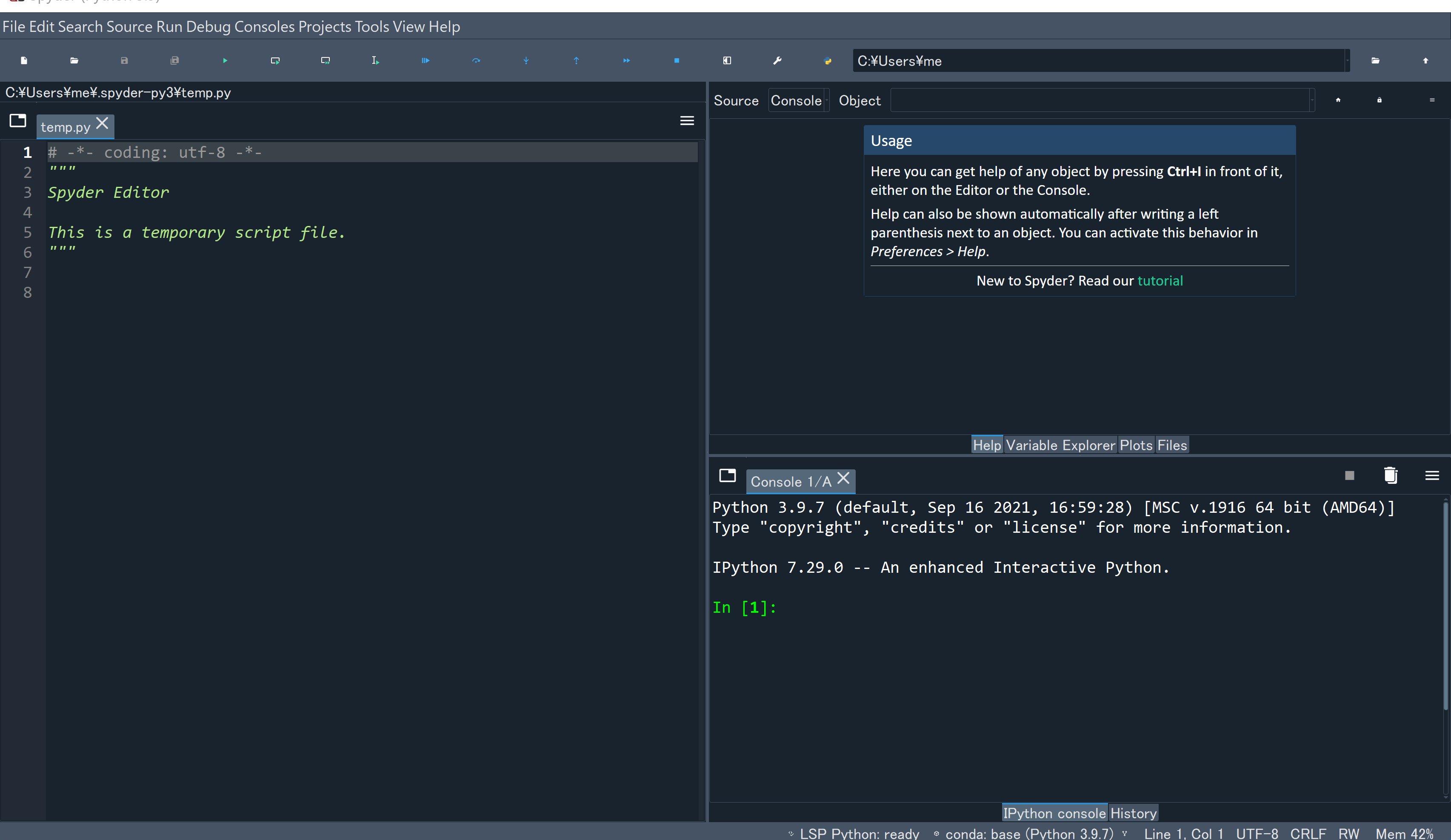
- Spyderは、Python開発環境である。
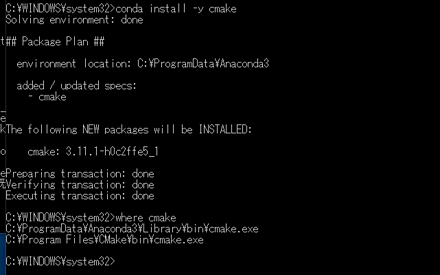
- condaは、Pythonのパッケージのインストール、各種ソフトウェアのインストール、新しいPython環境の作成等を行えるソフトウェアである。condaはAnaconda3の根幹となっている。
- Anaconda Promptは、コマンドラインインターフェイスである。
- Jupyter Notebookは、対話型のプログラム実行ツールである。Webブラウザで動作する。Python以外にもJulia、Ruby、R、Lua、LuaJIT、Haskell、Scala、Go、JavaScript、Node.js、Bashなどに対応している。
- Anaconda Navigatorは、アプリケーション管理ツールである。
関連する外部ページ
- Anaconda3の公式ページ: https://www.anaconda.com
- Anaconda3の公式ダウンロードページ: https://www.anaconda.com/download
- conda公式のチートシート: https://conda.io/projects/conda/en/latest/user-guide/cheatsheet.html
関連項目: Anaconda3のインストール(wingetを使用)(Windows上)
Anaconda3のインストール(wingetを使用)(Windows上)
- Windowsで、管理者権限でコマンドプロンプトを起動する。
- 次のコマンドを実行する。このコマンドは、Anaconda3をインストールし、パスを通すものである。
winget install --scope machine Anaconda.Anaconda3 powershell -command "$oldpath = [System.Environment]::GetEnvironmentVariable(\"Path\", \"Machine\"); $oldpath += \";C:\ProgramData\Anaconda3;C:\ProgramData\Anaconda3\Scripts\"; [System.Environment]::SetEnvironmentVariable(\"Path\", $oldpath, \"Machine\")"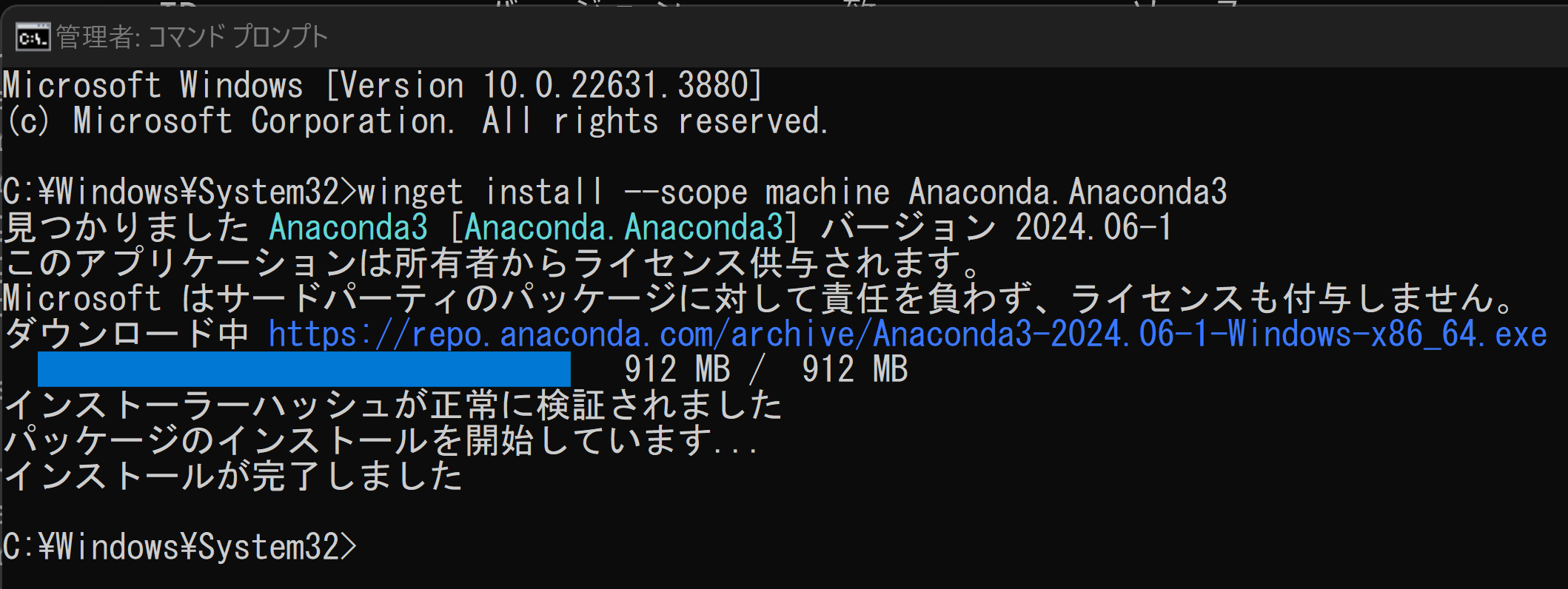
- Windowsのスタートメニューに「Anaconda3 (64-bit)」が追加され、その下に「Anaconda Navigator」、「Anaconda PowerShell Prompt」、「Anaconda Prompt」、「Jupyter Notebook」、「Reset Spyder Settings」、「Spyder」が表示される。
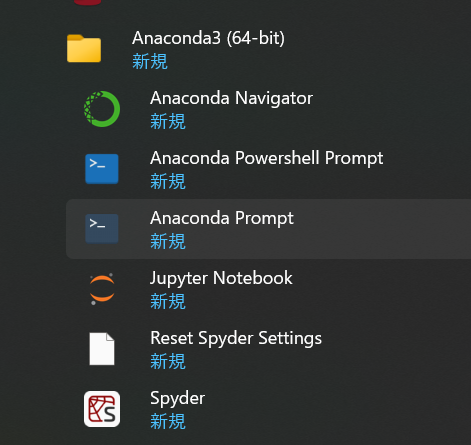
関連する外部ページ
- Anaconda3の公式ページ: https://www.anaconda.com
- Anaconda3の公式ダウンロードページ: https://www.anaconda.com/download
- conda公式のチートシート: https://conda.io/projects/conda/en/latest/user-guide/cheatsheet.html
サイト内の関連ページ
関連項目: Anaconda3
Anaconda3の使用上の注意点
Anaconda3でのパッケージ管理はpipではなくcondaを用いる。
Anaconda3のPythonのパスの設定
このサイトでは、システムの環境変数PATHの先頭部分に、次の5つが設定されているものとして説明している。
C:\ProgramData\Anaconda3 C:\ProgramData\Anaconda3\Library\mingw-w64\bin C:\ProgramData\Anaconda3\Library\usr\bin C:\ProgramData\Anaconda3\Library\bin C:\ProgramData\Anaconda3\Scripts
Anaconda Prompt
Anaconda Promptは、Anaconda3に同封されたコマンドプロンプトのソフトウェアである。Windowsのコマンドプロンプトとの違いは、conda関係の環境変数と、環境変数PYTHONIOENCODINGが自動設定されることである。
condaでPythonの隔離された環境
Pythonにはバージョンがある。Pythonには、さまざまなパッケージをインストールすることができる。condaの利用により、バージョンや搭載パッケージが異なる複数のPython環境を共存させることができる。
Windowsでは、Anaconda3に同封のcondaが便利である。
conda create --name py39 python=3.9
WindowsでのPythonとAnaconda内のPythonの共存
Anaconda3に内蔵のPythonを使いたいときは、pyコマンドは使わない。パスを通すか、フルパスで指定するか、Anaconda Promptを使う。
すでにPythonをインストール済みの場合でも、Anaconda3と両立できる。
- Anaconda3内のPythonは、孤立したPython環境である。
- Anaconda3の利用では、Anaconda Prompt、Spyderが便利である(いずれもスタートメニューから起動できる)。
- WindowsでPythonとAnaconda内のPythonが共存する場合、Anaconda3にパスを通すのは推奨できない。
Anaconda3ではpipを使わないこと。Anaconda3はpipの使用を想定していない。
WindowsのシステムのPythonについて、バージョンの異なるPythonを並列できる。バージョンの異なるPythonを使いたいだけのためにAnaconda3をインストールする必要はない。
conda
3. Google Colaboratory
Google Colaboratoryの使い方
スライド資料
3. (1) Google Colaboratoryの主な機能
Google Colaboratoryの利用により、オンラインで、Webブラウザを用いて、次のことができる。
- ノートブックの形式で、Pythonソースコードの編集や実行、実行結果の保存ができる。
- 説明文の編集ができる。説明文には、リンク、添付ファイル、図を含めることができる。
- 「!pip」、「%cd /content」などの、システム操作ができる。
- 共有機能により、第三者がノートブックをダウンロードし、実行できる。編集もできる。
Google Colaboratoryは、オンラインで使用する。Google Colaboratoryの使用には、Googleアカウントの取得が必要である。
「Colaboratoryへようこそ」のページのURL
https://colab.research.google.com/notebooks/welcome.ipynb?hl=ja
3. (2) Google Colaboratoryのプログラムを実行
- すべてのセルの実行を行うには、メニューで「ランタイム」、「すべてのセルを実行」と操作する。
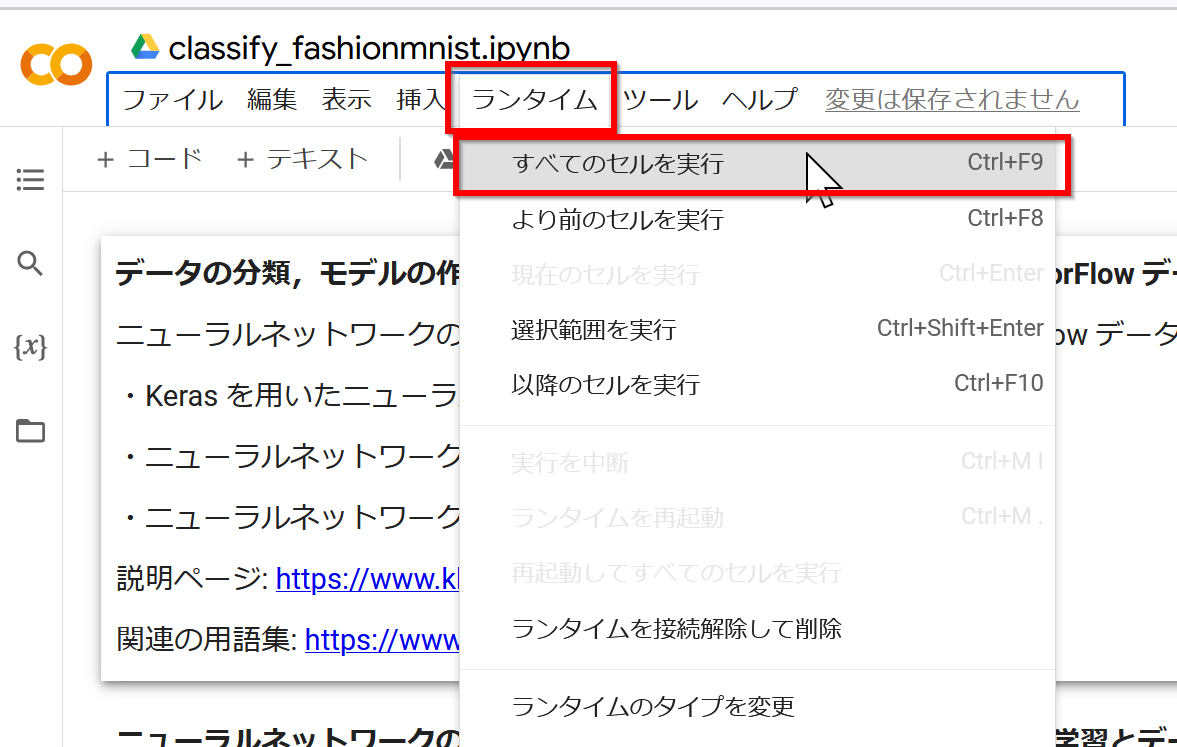
- Googleアカウントでのログインが求められたときはログインする。

- 実行がうまく行かない場合には、次を行う。
- Googleアカウントでログインしていないときは、ログインを行う。その後、再度、すべてのセルを実行する操作を行う。
- すべてのアクティブなセッションを停止する。その後、再度、すべてのセルを実行する操作を行う。そのために、メニューの「ランタイム」、「セッションの管理」と操作する。アクティブなセッションの一覧が表示されるので、「終了」をクリックして、すべてのアクティブなセッションを終了する。
3. (3) Google ColaboratoryでPython 3の新しいノートブックを新規作成
Google ColaboratoryはオンラインのPython開発環境である。使用するにはGoogleアカウントが必要である。
- Google ColaboratoryのWebページを開く。
- 「ファイル」で、「ノートブックを新規作成」を選ぶ。
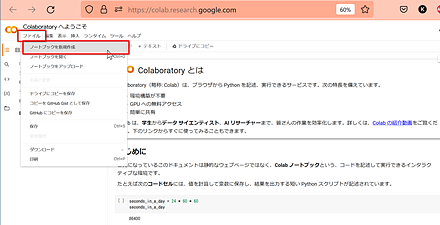
- Googleアカウントでのログインが求められたときはログインする。

- コードセルの中にPythonプログラムを書き、「実行ボタン」をクリックする。
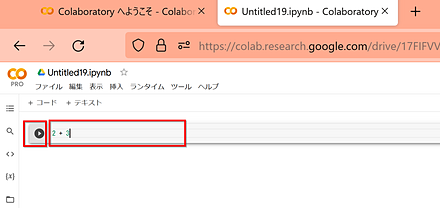
- コードセルを追加したいときは、「挿入」で、「コードセル」をクリックする。
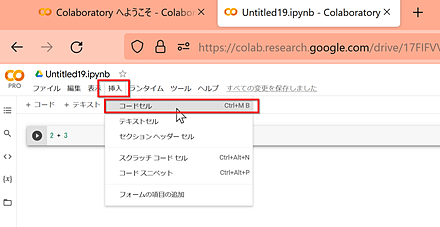
3. (4) Google Colaboratoryでファイルのアップロードとダウンロード
ファイルのアップロード
ファイルのアップロードを行うには、次のコードを使用する。
from google.colab import files
uploaded = files.upload()
for fname in uploaded.keys():
print(fname)
ディレクトリを新規作成し、そこにファイルをアップロードする場合は、次のコードを使用する。
from google.colab import files
import os
import shutil
udir = 'upload'
if os.path.isdir(udir):
shutil.rmtree(udir)
os.mkdir(udir)
uploaded = files.upload()
for fname in uploaded.keys():
print(fname)
ファイルのダウンロード
from google.colab import files
files.download('filename')
3. (5) Google ColaboratoryでTensorFlow、Kerasのバージョン確認
Google Colaboratoryのコードセルで、次のPythonプログラムを実行する。
import tensorflow as tf
print(tf.__version__)
import keras
print(keras.__version__)
3. (6) Google ColaboratoryでNVIDIA CUDAのバージョン確認
Google Colaboratoryのコードセルで、次のPythonプログラムを実行する。
!nvcc -V
3. (7) Google ColaboratoryでGPUの確認
!nvidia-smi --query-gpu=gpu_name,driver_version,memory.total --format=csv

3. (8) Google Colaboratoryを使用中であるかを判別するPythonプログラム
try:
from google.colab import drive
USE_COLAB = True
except:
USE_COLAB = False
Google Colaboratoryでの実行結果は次のとおりである。
Windowsのコマンドプロンプトでの実行結果は次のとおりである。
3. (9) Google Colaboratoryでの画像表示
Google Colaboratoryのcv2_imshowを使用する方法である(Google Colaboratoryでのみ動作する)。
%cd /content
!curl -O http://images.cocodataset.org/val2017/000000439715.jpg
import cv2
from google.colab.patches import cv2_imshow
img = cv2.imread("000000439715.jpg")
cv2_imshow(img)
cv2.waitKey(0)
cv2.destroyAllWindows()
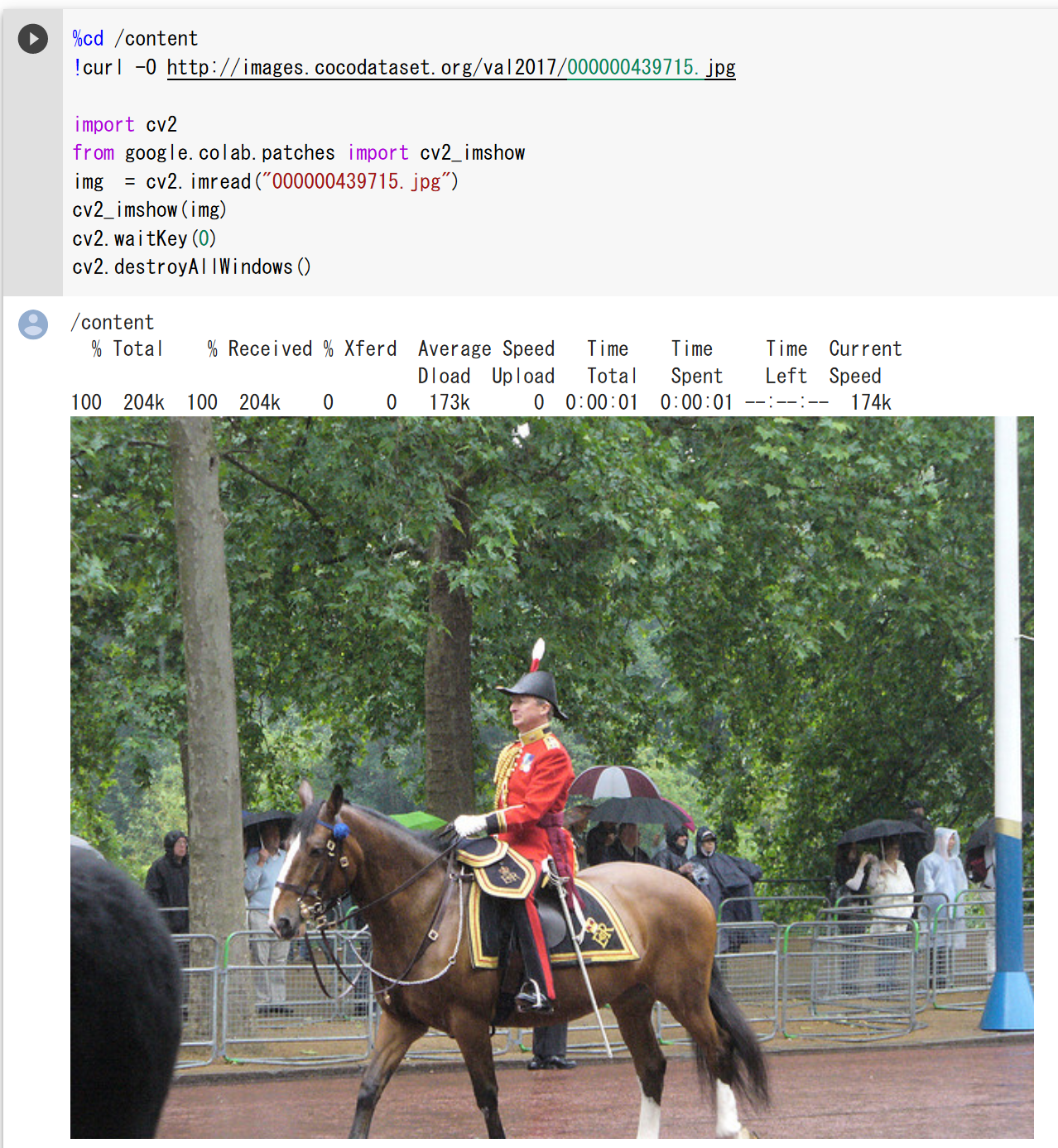
PILのImageを使用する方法である(IPython.displayのImageではない)。
%cd /content
!curl -O http://images.cocodataset.org/val2017/000000439715.jpg
from PIL import Image
Image.open('000000439715.jpg').show()
3. (10) Google Colaboratoryでの画像ファイルの表示
matplotlib.pyplotのimshowを使用する方法である。
見本1つめは次のとおりである。
%cd /content
!curl -O http://images.cocodataset.org/val2017/000000439715.jpg
import cv2
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
img = cv2.imread("000000439715.jpg")
plt.style.use('default')
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
plt.show()
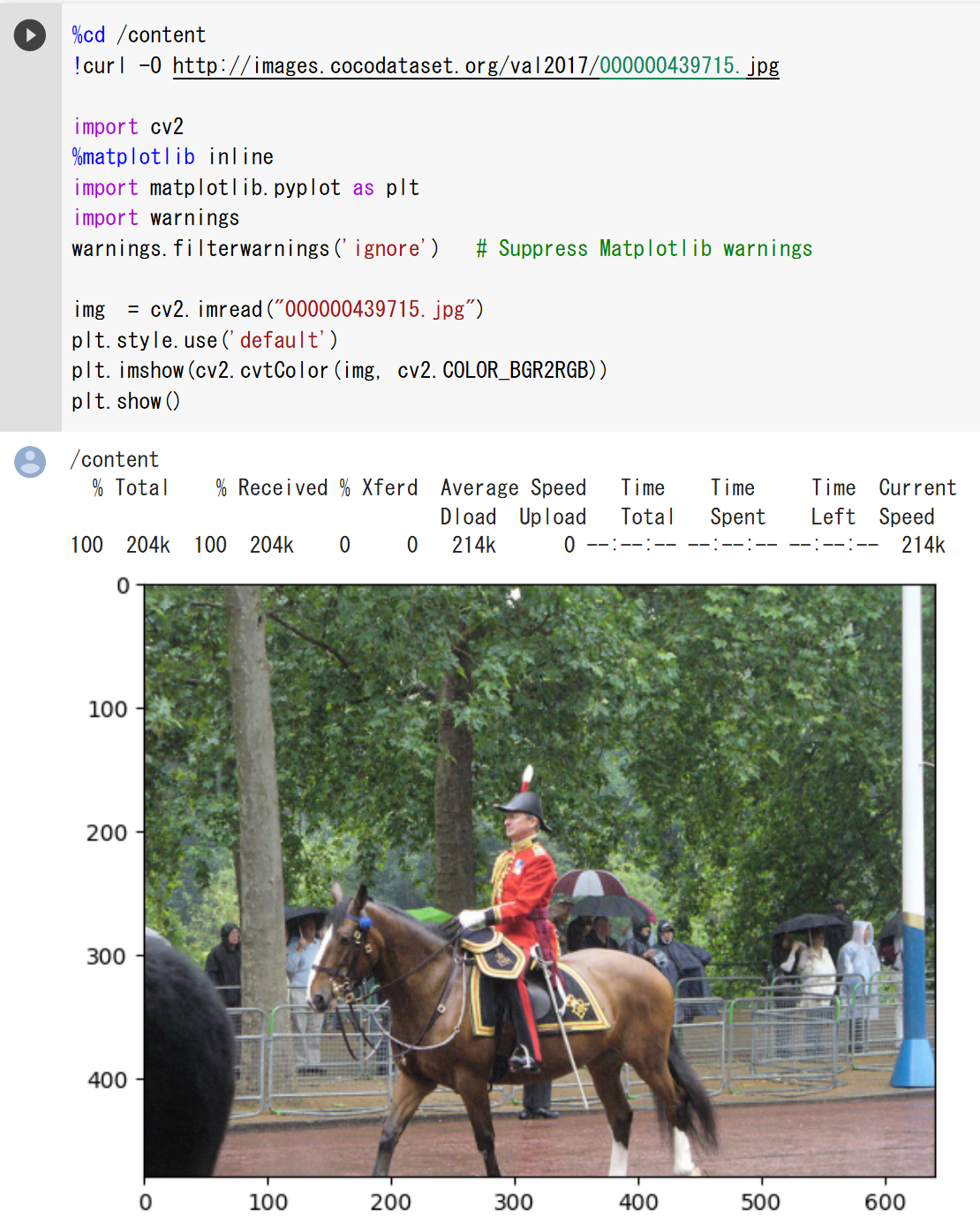
見本2つめは次のとおりである。
%cd /content
!curl -O http://images.cocodataset.org/val2017/000000439715.jpg
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import os
os.environ["MPLBACKEND"] = "Agg"
fpath = '000000439715.jpg'
plt.imshow(mpimg.imread(fpath))
plt.axis('off')
plt.show()
3. (11) Google Colaboratoryでの動画像の表示
from IPython.display import HTML
from base64 import b64encode
def show_mp4(video_path, width=640, height=480):
with open(video_path, "rb") as video_file:
video_data = video_file.read()
video_base64 = b64encode(video_data).decode()
video_url = f"data:video/mp4;base64,{video_base64}"
video_html = f"""
<video width="{width}" height="{height}" autoplay loop controls>
<source src="{video_url}">
</video>
"""
return HTML(video_html)
show_mp4("hoge.mp4")
3. (12) その他
Google ColaboratoryでのDetectron2のインストールは次のとおりである。
!python -m pip install pyyaml==5.1
import sys, os, distutils.core
!git clone --recursive https://github.com/facebookresearch/detectron2
dist = distutils.core.run_setup("./detectron2/setup.py")
!python -m pip install {' '.join([f"'{x}'" for x in dist.install_requires])}
!python -m pip install 'git+https://github.com/facebookresearch/detectron2.git'
4. Pythonプログラムの例とGoogle Colaboratoryでの実行結果
4. (1) 三角関数のプロット
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
plt.style.use('ggplot')
x = np.linspace(0, 6, 100)
plt.style.use('default')
plt.plot(x, np.sin(x))
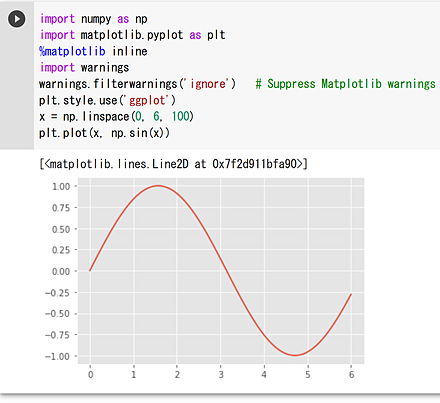
4. (2) 折れ線グラフのプロット
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
plt.style.use('ggplot')
x = [1, 2, 3, 4]
y = [3, 5, 2, 4]
plt.plot(x, y)
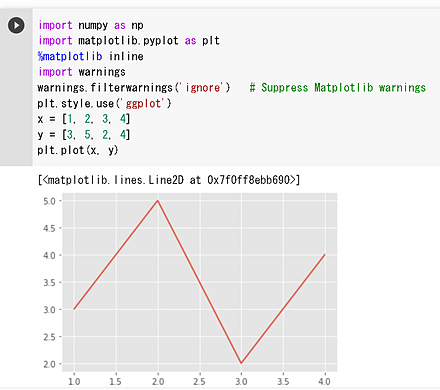
4. (3) 散布図のプロット
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
plt.style.use('ggplot')
x = [1, 2, 3, 4]
y = [3, 5, 2, 4]
plt.scatter(x, y)
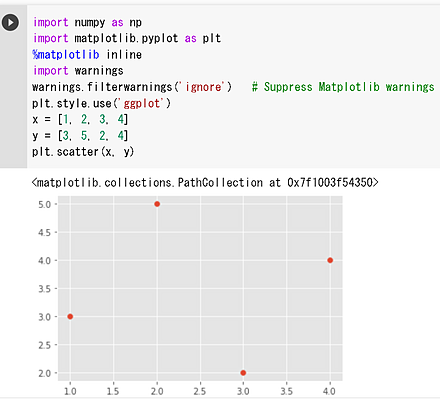
4. (4) 画像ファイルの表示
mmcvを使用する方法である。前準備としてmmcvのインストールが必要である。
import mmcv
mmcv.imshow('000000439715.jpg')
4. (5) 画像ファイルのダウンロード、画像ファイル保存、表示
from PIL import Image
import requests
from IPython.display import display
url = 'https://github.com/pytorch/hub/raw/master/images/dog.jpg'
response = requests.get(url)
img = Image.open(requests.get(url, stream=True).raw)
display(img)
img.save('dog.jpg')
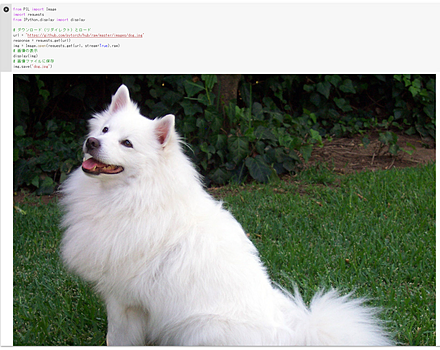
4. (6) 行列の積、主成分分析、SVD、k-Meansクラスタリング
このプログラムは、NumPyとscikit-learnを使用して行列計算と機械学習タスクを実行し、その処理時間を測定している。具体的には、行列の積、主成分分析、特異値分解(SVD)、k-meansクラスタリングを行っている。
import time
import numpy
import numpy.linalg
import sklearn.decomposition
import sklearn.cluster
X = numpy.random.rand(2000, 2000)
Y = numpy.random.rand(2000, 2000)
a = time.time(); Z = numpy.dot(X, Y); print(time.time() - a)
pca = sklearn.decomposition.PCA(n_components = 2)
a = time.time(); pca.fit(X); X_pca = pca.transform(X); print(time.time() - a)
a = time.time(); U, S, V = numpy.linalg.svd(X); print(time.time() - a)
a = time.time();
kmeans_model = sklearn.cluster.KMeans(n_clusters=10, random_state=10).fit(X)
labels = kmeans_model.labels_
print(time.time() - a)
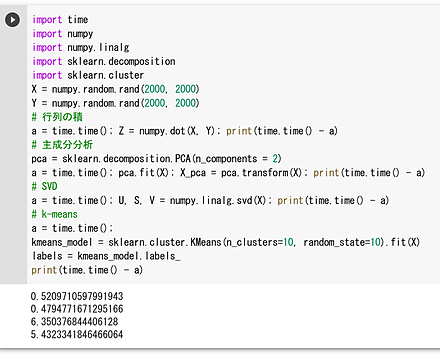
4. (7) ConvNeXt
ImageNetで学習済みのConvNeXtBaseモデルを用いた画像分類を行う。
- パソコン接続のカメラを使用するので準備しておく。
- 前準備としてPython用opencv-pythonのインストールを行う。
python -m pip install -U opencv-python opencv-contrib-python - Windowsで、コマンドプロンプトを実行する。
- エディタを起動する。
cd /d c:%HOMEPATH% notepad convnext.py - エディタで、次のプログラムを保存する。このプログラムは、TensorFlow、ConvNeXtBaseモデルを活用し、カメラから取得した画像をリアルタイムで画像分類する。プログラムでは、GPUの設定、モデルのロード、フレームの前処理、画像分類、結果と推論に要した時間を表示する。
import tensorflow as tf from tensorflow.keras.applications import ConvNeXtBase import numpy as np import time import cv2 def set_gpu_config(): physical_devices = tf.config.list_physical_devices('GPU') if len(physical_devices) > 0: print("GPU available:", physical_devices) for device in physical_devices: tf.config.experimental.set_memory_growth(device, True) else: print("No GPU found. Running on CPU.") def preprocess_image(img): img = cv2.resize(img, (224, 224)) img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) img = np.expand_dims(img, axis=0) img = tf.keras.applications.convnext.preprocess_input(img) return img def load_model(): return ConvNeXtBase(weights='imagenet') def classify_camera_frames(model): cap = cv2.VideoCapture(0) while cap.isOpened(): ret, frame = cap.read() if not ret: break img = preprocess_image(frame) start_time = time.perf_counter() preds = model.predict(img) end_time = time.perf_counter() prediction_time = end_time - start_time top_pred_index = np.argmax(preds) class_label = tf.keras.applications.convnext.decode_predictions(preds, top=1)[0][0][1] confidence = preds[0][top_pred_index] cv2.putText(frame, f"Class: {class_label}", (10, 30), cv2.FONT_HERSHEY_SIMPLEX, 0.9, (0, 255, 0), 2) cv2.putText(frame, f"Confidence: {confidence:.4f}", (10, 70), cv2.FONT_HERSHEY_SIMPLEX, 0.9, (0, 255, 0), 2) cv2.putText(frame, f"Time: {prediction_time:.4f} seconds", (10, 110), cv2.FONT_HERSHEY_SIMPLEX, 0.9, (0, 255, 0), 2) cv2.imshow("Camera Classification", frame) if cv2.waitKey(1) & 0xFF == ord('q'): break cap.release() cv2.destroyAllWindows() def main(): set_gpu_config() model = load_model() classify_camera_frames(model) if __name__ == '__main__': main()
- Pythonプログラムの実行を行う。
Pythonプログラムの実行方法は次のとおりである。
- Windowsではpython(Pythonランチャーはpy)
- Ubuntuではpython3
サイト内の関連ページ: Pythonのまとめ: 別ページ
プログラムをconvnext.pyのようなファイル名で保存したので、「python convnext.py」のようなコマンドで実行する。
python convnext.py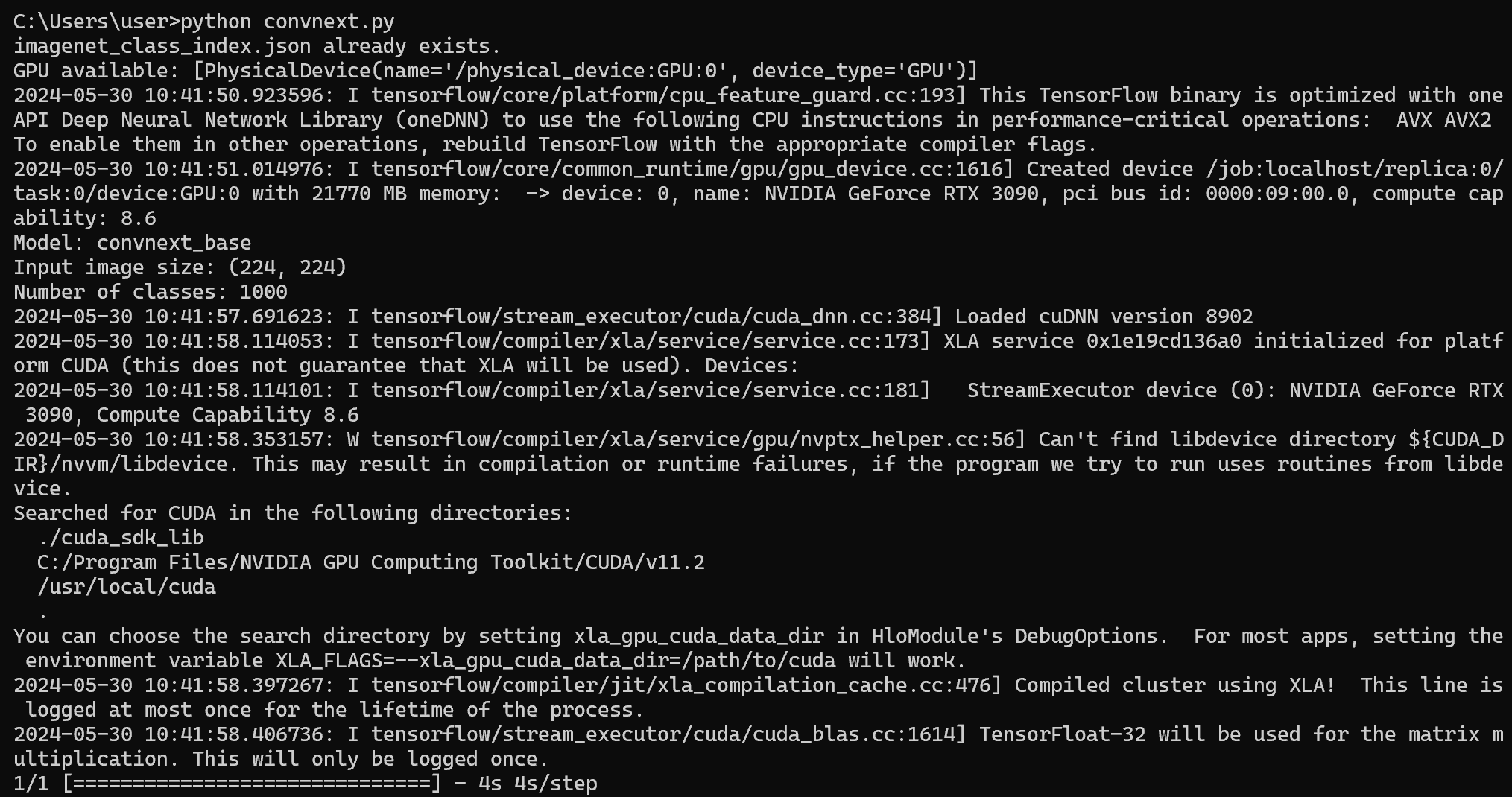
- 結果の確認を行う。終了はqキーである。

4. (8) 空白などで区切られたテキストをリストに変換
import re
def removeletters(s):
return re.sub(r':|\||-', ' ', s)
def getdata(s):
m = re.match(r'[0-9]+(b|B|k|K|m|M|g|G|t|T)*', s)
if m:
return m.group()
else:
return ''
s = 'system 07-09 15:00:03| 0 0 100 0 0: 0 0 100 0 0: 0 0 100 0 0: 0 0 100 0 0: 1 0 99 0 0: 0 0 100 0 0: 0 0 100 0 0: 0 0 100 0 0| 0 40k| 173 243 |0.03 0.05 0|1856M 14.1G 1553M 13.1G'
a = removeletters(s)
b = a.split()
print(list(map(getdata, b)))

5. Python 関係のツール
5. (1) pip
pipはPythonのパッケージマネージャである。
Windows
- pipの起動は「pip」または「python -m pip」である。
- Windowsのユーザ名で日本語を使っているときは、コマンドプロンプトを管理者として実行してから、「pip」または「python -m pip」を実行する。
- venvを使うときは、venvが定めるactivateを実行した後に「pip」または「python -m pip」を実行する。
Ubuntu
- システムPythonを使っていて、隔離したPython環境を作らない(pyenv、venvなども使っていない)ときは、pipではなくて、aptでインストールする。
- pyenvを使うときは、「pyenv shell <バージョン>」のあとに「pip」または「python -m pip」を実行する。
- venvを使うときは、venvが定めるactivateを実行した後に「pip」または「python -m pip」を実行する。
5. (2) Python パッケージ・インデックス (PyPI)
パッケージの検索や調査を行うときに、次のURLを使う。
Python パッケージ・インデックス (PyPI) の URL: https://pypi.org/
5. (3) Google Colaboratory での pip の操作
Google Colaboratoryではpipを次のように操作する。頭に「!」を付ける。
- パッケージのインストール
!pip3 install <パッケージ名>パッケージのバージョン指定を行うときは、パッケージ名(例えば「numpy」)の後に、「numpy==19.5」のように付ける。
- インストール済みパッケージの一覧
!pip3 list - アンインストール
!pip3 uninstall <パッケージ名> - パッケージの情報
!pip3 show <パッケージ名>
5. (4) Windows での pip の操作
Windowsではpipを次のように操作する。
- Python のバージョン指定なし
Windowsで複数のPythonをインストールしているときは、環境変数Pathで先頭のPythonが使用される。
- パッケージのインストール
pip install <パッケージ名>Windowsで、管理者の領域にPythonをインストールしている場合には、管理者の権限で実行する。
パッケージのバージョン指定を行うときは、パッケージ名(例えば「numpy」)の後に、「numpy==19.5」のように付ける。
- インストール済みパッケージの一覧
pip list - アンインストール
pip uninstall <パッケージ名>Windowsで、管理者の領域にPythonをインストールしている場合には、管理者の権限で実行する。
- パッケージの情報
pip show <パッケージ名>
- パッケージのインストール
- WindowsのPython ランチャーでPythonのバージョン指定
- パッケージのインストール
py -3.10 -m pip install <パッケージ名> (Python 3.10 の pip を使う場合)Windowsで、管理者の領域にPythonをインストールしている場合には、管理者の権限で実行する。
パッケージのバージョン指定を行うときは、パッケージ名(例えば「numpy」)の後に、「numpy==19.5」のように付ける。
- インストール済みパッケージの一覧
py -3.10 -m pip list (Python 3.10 の pip を使う場合) - アンインストール
py -3.10 -m pip uninstall <パッケージ名> (Python 3.10 の pip を使う場合)Windowsで、管理者の領域にPythonをインストールしている場合には、管理者の権限で実行する。
- パッケージの情報
py -3.10 -m pip show <パッケージ名> (Python 3.10 の pip を使う場合)
- パッケージのインストール
venvを使うときは、venvが定めるactivateコマンドを実行した後、「python」で起動する。
5. (5) Ubuntu での pip の操作
UbuntuでシステムPythonを使う場合は、pipを次のように操作する。
- パッケージのインストール
sudo pip3 install <パッケージ名> (システムPythonを使う場合)Ubuntuでは、「sudo pip3 install」でパッケージをインストールする前に、「apt-cache search <キーワード>」でUbuntuのパッケージを検索し、Ubuntuパッケージが見つかった場合にはそちらを「apt install <UbuntuのパッケージA名>」でインストールする。
パッケージのバージョン指定を行うときは、パッケージ名(例えば「numpy」)の後に、「numpy==19.5」のように付ける。
- インストール済みパッケージの一覧
pip3 list (システムPythonを使う場合) - アンインストール
sudo pip3 uninstall <パッケージ名> (システムPythonを使う場合) - パッケージの情報
pip3 show <パッケージ名> (システムPythonを使う場合)
pyenvを用いてインストールしたPythonは、pyenvの設定の後、「python」で起動する。
venvを使うときは、venvが定めるactivateコマンドを実行した後、「python」で起動する。
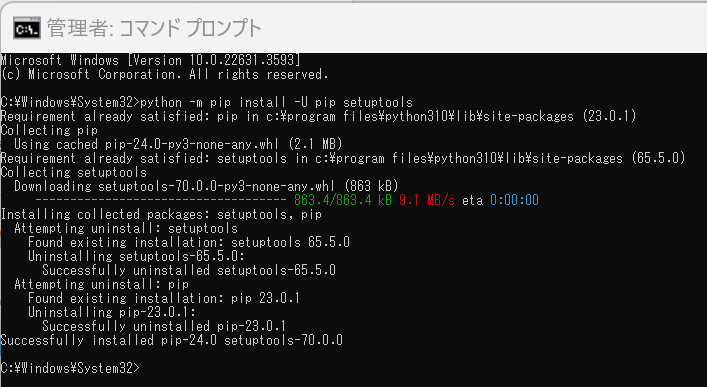
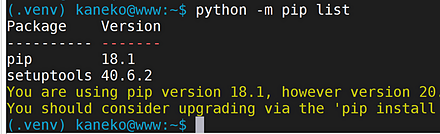
5. (6) pip と setuptools を最新版に更新
- Windowsの場合
Windowsでは、コマンドプロンプトを管理者として開き次のコマンドを実行する。
python -m pip install -U pip setuptools - Ubuntuの場合
sudo apt -y upgrade python3-pip python3-setuptools
5. (7) pip のインストールを手動で行いたい場合
Pythonをインストールするとpipがインストールされるので、ここに書いた操作は通常は必要ない。
- Windowsでpypaを使ってpipの更新を行う操作
cd /tmp curl -O https://bootstrap.pypa.io/get-pip.py python get-pip.py - 次のページから.whl形式ファイルをダウンロードしてpipでインストールする場合もある
「Geospatial library wheels for Python on Windows」のページ: https://github.com/cgohlke/geospatial-wheels
5. (8) Python の setup.py の実行
次のような操作になる。「pip」のところは、Ubuntuでは必要に応じて「pip3」に読み替えること。
git clone https://github.com/openai/gym
cd gym
pip install -e .
必要に応じて、「pip install -e .」の代わりに、次のように操作する。
git clone https://github.com/openai/gym
cd gym
python setup.py build
python setup.py install
python setup ... にオプションを付けたいときは「--set CMAKE_PREFIX_PATH="c:\dlib"」のように付け加える。
Windowsでは、setup.pyの実行前に、次のようなコマンドを実行し、環境変数などを設定できる場合がある。
set MSVC_VERSION=16
set CMAKE_GENERATOR=Visual Studio 16 2019
set PREBUILD_COMMAND=vcvarsall.bat
set PREBUILD_COMMAND_ARGS=x64
# call "vcvarsall.bat" x64 -vcvars_ver=14.11
Pythonのsetup.pyを用いて、wheel形式のpipパッケージを作成したいとき。
python -m pip install wheel
python setup.py bdist_wheel
5. (9) Python の build_ext の実行
Pythonのpipコマンドで、pillowをソースコードからビルドしている例である。
python -m pip install pillow==6 --global-option="build_ext" --global-option="--disable-jpeg" --global-option="--disable-zlib"
pillowのソースコードをダウンロードし、ビルドしている例である。
cd c:\pytools
git clone https://github.com/python-pillow/Pillow
cd Pillow
python setup.py build_ext --disable-zlib --disable-jpeg install
5. (10) Geospatial library wheels for Python on Windows
「Geospatial library wheels for Python on Windows」のページ
https://github.com/cgohlke/geospatial-wheels
5. (11) 2to3
2to3は、Pythonバージョン2用のソースコードをPythonバージョン3用に変換するプログラムである。次のように実行する。
2to3 -w .
Windowsで2to3が動かないとき、環境変数PATHの設定により動くようになる。
システムの環境変数PATHに、「C:\Program Files\Python\Python310\Tools\scripts」を加える。「C:\Program Files\Python\Python310」は、実際にPythonをインストールしたディレクトリに読み替えること。
Windowsで次のようにフルパスを書いて実行してもよい。
python %LOCALAPPDATA%\Programs\Python\Python310\Tools\scripts\2to3.py -w .
6. Python 開発環境、Python コンソール(Jupyter Qt Console、Jupyter ノートブック (Jupyter Notebook)、Jupyter Lab、Nteract、spyder、PyCharm)
Pythonプログラムを動かして、結果をビジュアルに見たいときは、Pythonの開発環境やPythonコンソール(Jupyter Qt Console、Spyder、PyCharm、PyScripterなど)が便利である。
6. (1) Python、pip、Python 開発環境、Python コンソールのコマンドでの起動
Python、pip、Python開発環境の起動コマンドのまとめである。
Windowsの場合
Windowsで複数のPythonをインストールしているときは、環境変数Pathで先頭のPythonが使用される。
- python: python
- pip: python -m pip または pip
- Jupyter Qt Console: jupyter qtconsole あるいは python -m jupyter qtconsole
- Jupyter ノートブック (Jupyter Notebook): jupyter notebook
- Jupyter Lab: jupyter lab あるいは python -m jupyter lab
- Nteract: jupyter nteract あるいは python -m jupyter nteract
- Spyder: spyder
WindowsのPythonランチャーでバージョン指定する場合
- インストール済みPythonのバージョン一覧: py -0
- python: py -3.10 (Python 3.10 を使う場合)
- pip: py -3.10 -m pip (Python 3.10 の pip を使う場合)
- Jupyter Qt Console: py -3.10 -m qtconsole (Python 3.10 を使う場合)
- Jupyter ノートブック (Jupyter Notebook): py -3.10 -m notebook (Python 3.10 を使う場合)
- Jupyter Lab: py -3.10 -m jupyterlab (Python 3.10 を使う場合)
Ubuntuの場合
- python: python3
- pip: sudo pip3
- Jupyter Qt Console: jupyter qtconsole あるいは python -m jupyter qtconsole
- Jupyter ノートブック (Jupyter Notebook): jupyter notebook
- Jupyter Lab: jupyter lab あるいは python -m jupyter lab
- Nteract: jupyter nteract あるいは python -m jupyter nteract
- Spyder: spyder
6. (2) Windows での Python 開発環境として、Jupyter Qt Console、Jupyter ノートブック (Jupyter Notebook)、Jupyter Lab、Nteract、spyder のインストール
Pythonのバージョン指定なし
Windowsで複数のPythonをインストールしているときは、環境変数Pathで先頭のPythonが使用される。
- Pythonコンソール(Jupyter Qt Console)、Jupyter ノートブック (Jupyter Notebook)、Jupyter Lab、Nteract、spyderのインストール
Windowsでは、コマンドプロンプトを管理者として実行し、次のコマンドを実行する。
python -m pip install -U pip setuptools requests notebook==6.5.7 jupyterlab jupyter jupyter-console jupytext PyQt5 nteract_on_jupyter spyder
- WindowsでのPyCharmのインストールは、別ページで説明している。
- WindowsでのPyScripterのインストールは、別ページで説明している。
WindowsのPythonランチャーでPythonのバージョン指定
使用するPythonのバージョンを指定する。Python 3.10 を使う場合は、コマンドプロンプトを管理者として開き次のコマンドを実行する。
py -3.10 -m pip install -U pip setuptools requests jupyterlab jupyter jupyter-console jupytext PyQt5 nteract_on_jupyter spyder
6. (3) Ubuntu での Python 開発環境として、Jupyter Qt Console、Jupyter ノートブック (Jupyter Notebook)、Jupyter Lab、Nteract、spyder のインストール
Ubuntuでインストールを行うには、次のコマンドを実行する。
# パッケージリストの情報を更新
sudo apt update
sudo apt -y install python-is-python3 python3-dev python-dev-is-python3 python3-pip python3-setuptools python3-venv build-essential
sudo pip3 uninstall -y ptyprocess sniffio terminado tornado jupyterlab jupyter jupyter-console jupytext nteract_on_jupyter spyder
sudo apt -y install jupyter jupyter-qtconsole spyder3
sudo apt -y install python3-ptyprocess python3-sniffio python3-terminado python3-tornado
sudo pip3 install -U jupyterlab jupyter jupyter-console jupytext nteract_on_jupyter
Ubuntuで複数のPythonバージョンを共存しているときは、pyenvを使う。次のようにバージョン指定する。
pyenv shell 3.8.3
python -m pip install jupyterlab jupyter jupyter-console jupytext
6. (4) Python コンソール
Pythonコンソールは、Pythonのシェルの画面のことである。プロンプトが出て、Pythonのプログラムを受け付ける。そして、その実行結果を表示する。
- Jupyter Qt Console : Pythonコンソールの機能を持つ
- Spyder: Pythonコンソールの機能を持つ(デフォルトで右下の画面がPythonコンソールになっている)
- PyCharm: Pythonコンソールの機能を持つ
- python
Windowsでは、端末で「python」あるいは「py -3.10(Python 3.10 を使う場合)」を実行して起動する。
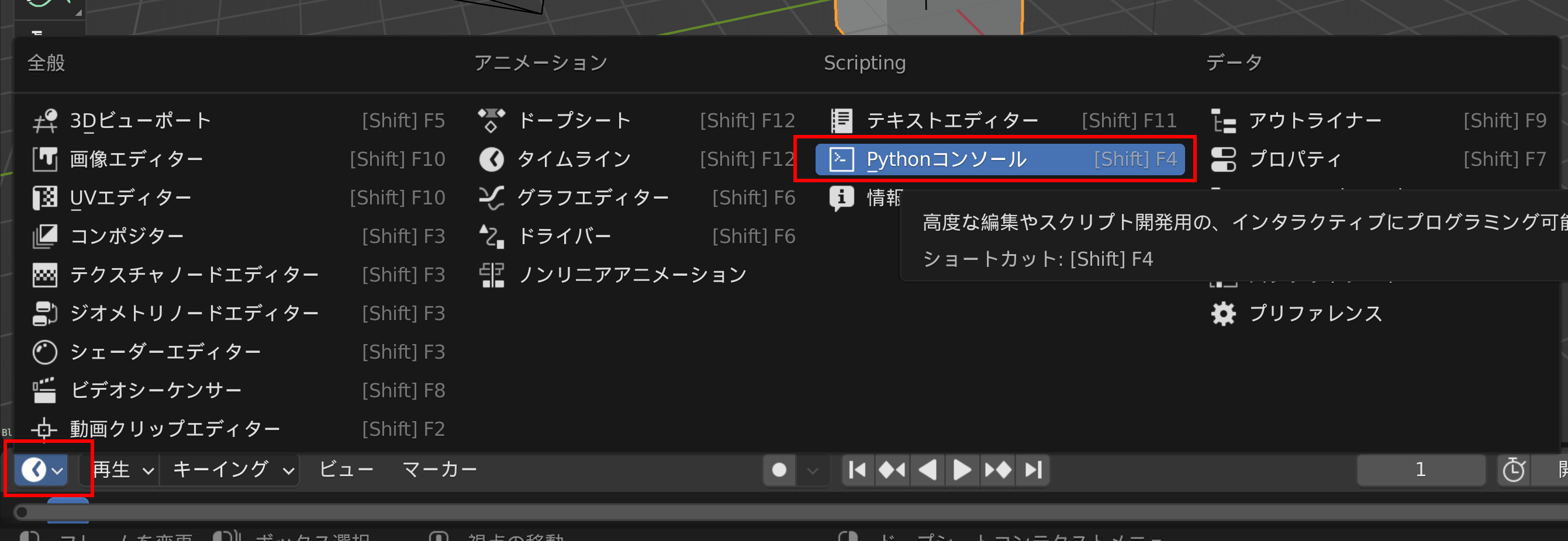
Blender の Python コンソール
Blenderに内蔵されたPythonのコンソールである。Blender 3.0では次の手順で開くことができる。
画面として「Pythonコンソール」を選ぶ。
6. (5) Jupyter Qt Console
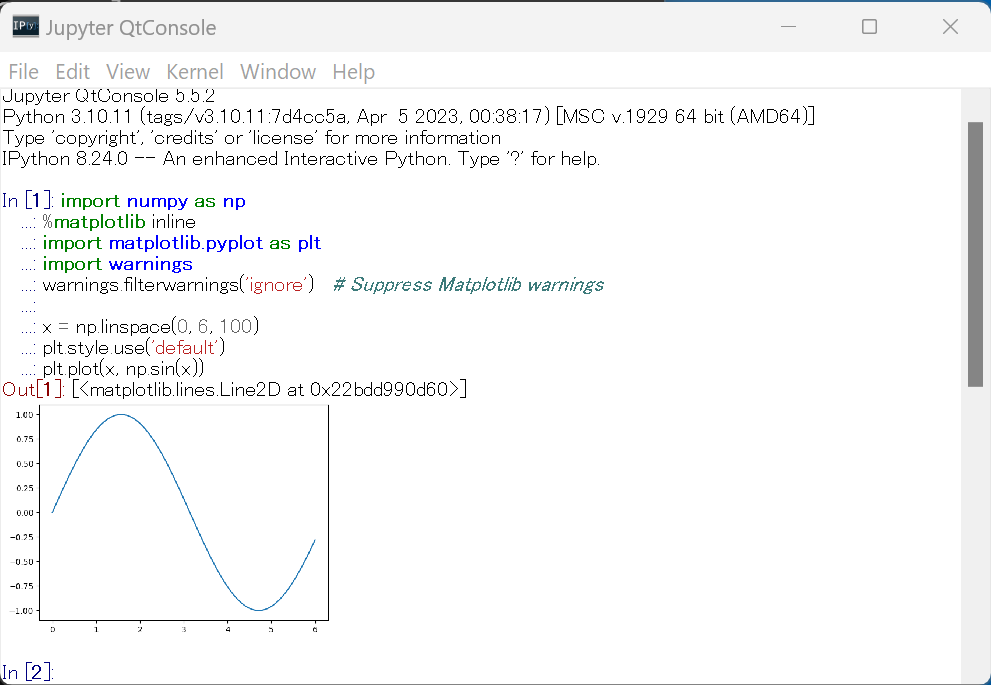
Jupyter Qt ConsoleはPythonコンソールの機能を持ったソフトウェアである。インストールは、このページの別の項目で説明している。
Jupyter Qt Consoleの起動は、「jupyter qtconsole」または「py -3.10 -m qtconsole」(Python 3.10 を使う場合)である。
次のPythonプログラムを実行してみる。
次のプログラムは、NumPyとMatplotlibを使用して、0から6までの範囲のsin関数のグラフを描画する。warningsモジュールを使用してMatplotlibの警告表示を抑制し、Matplotlibでは、デフォルトのスタイルを使用する。
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore') # Suppress Matplotlib warnings
x = np.linspace(0, 6, 100)
plt.style.use('default')
plt.plot(x, np.sin(x))
6. (6) Jupyter ノートブック (Jupyter Notebook)
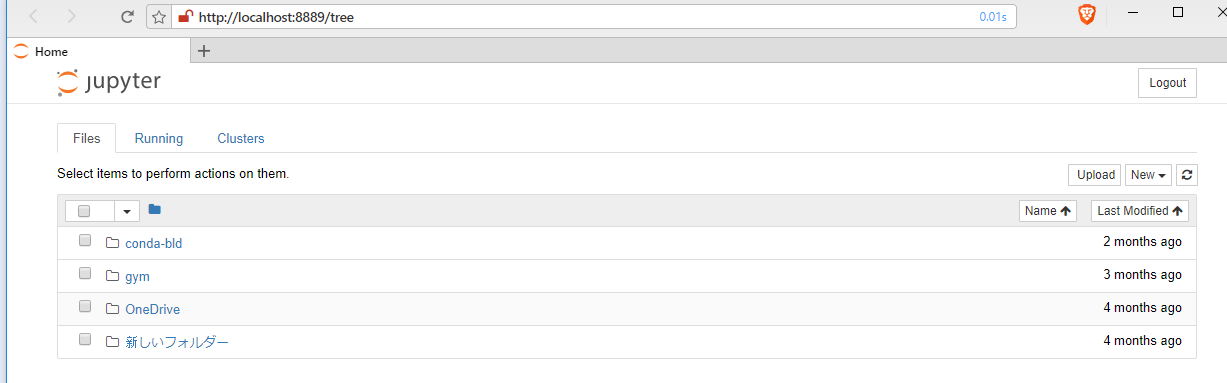
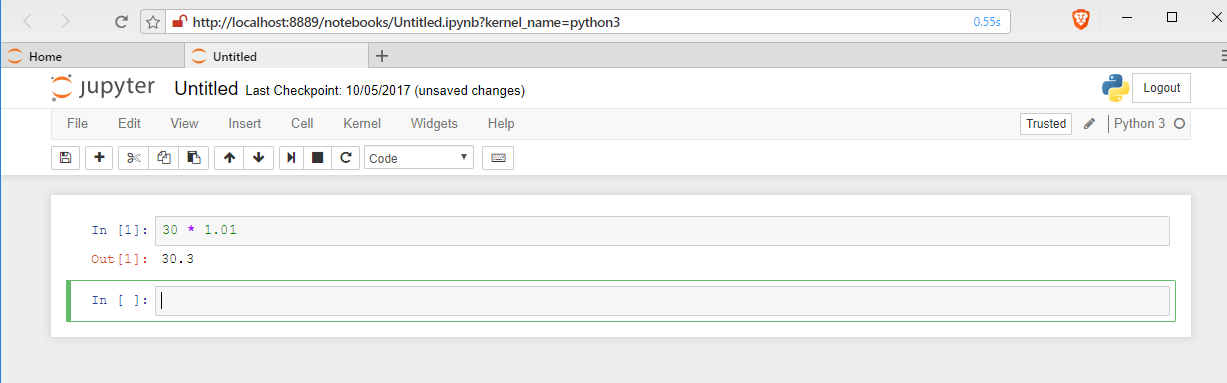
Jupyter ノートブックは、Pythonなどのプログラムのソースコード、実行結果などを1つのノートとして残す機能をもったノートブックである。インストールは、このページの別の項目で説明している。
Jupyter ノートブック (Jupyter Notebook)の起動は、「jupyter notebook」または「py -3.10 -m notebook」(Python 3.10 を使う場合)である。
6. (7) Jupyter Lab
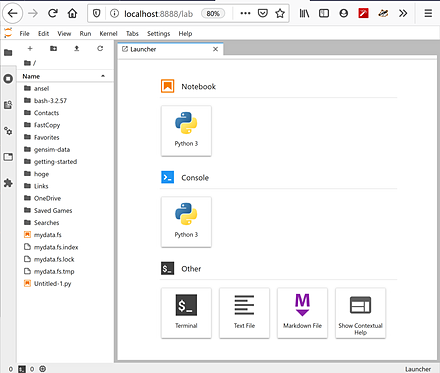
Jupyter LabはPythonプログラム作成に関する種々の機能を持ったソフトウェアである。インストールは、このページの別の項目で説明している。
Jupyter Labの起動は、「jupyter lab」または「py -3.10 -m jupyterlab」(Python 3.10 を使う場合)である。
pyenvを使うときは、次のようにバージョン指定する。
JupyterLabの起動は、「pyenv shell <バージョン>; jupyter lab」である。Jupyter Qt Consoleの起動は、「pyenv shell <バージョン>; jupyter qtconsole」である。
6. (8) Nteract
Nteractは、Pythonなどのプログラムのソースコード、実行結果などを1つのノートとして残す機能をもったノートブックである。インストールは、このページの別の項目で説明している。
Nteractの起動は、「jupyter nteract」である。
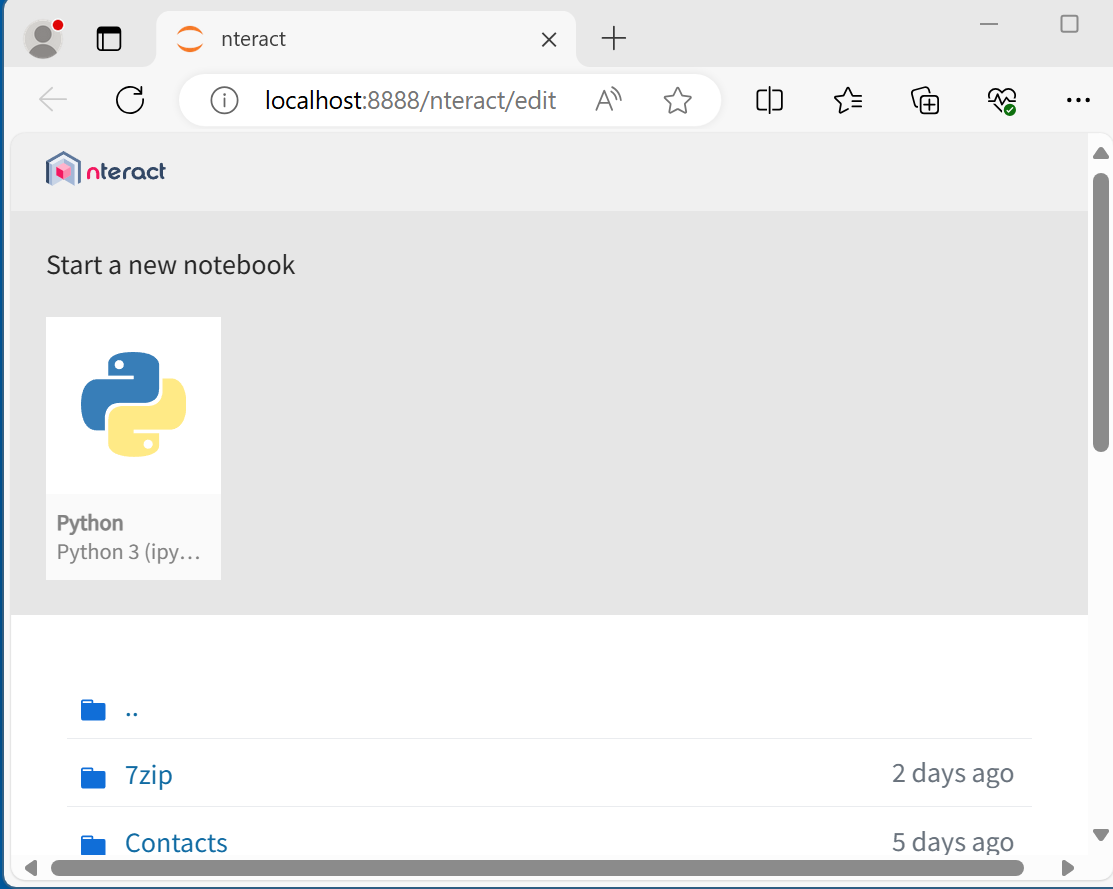
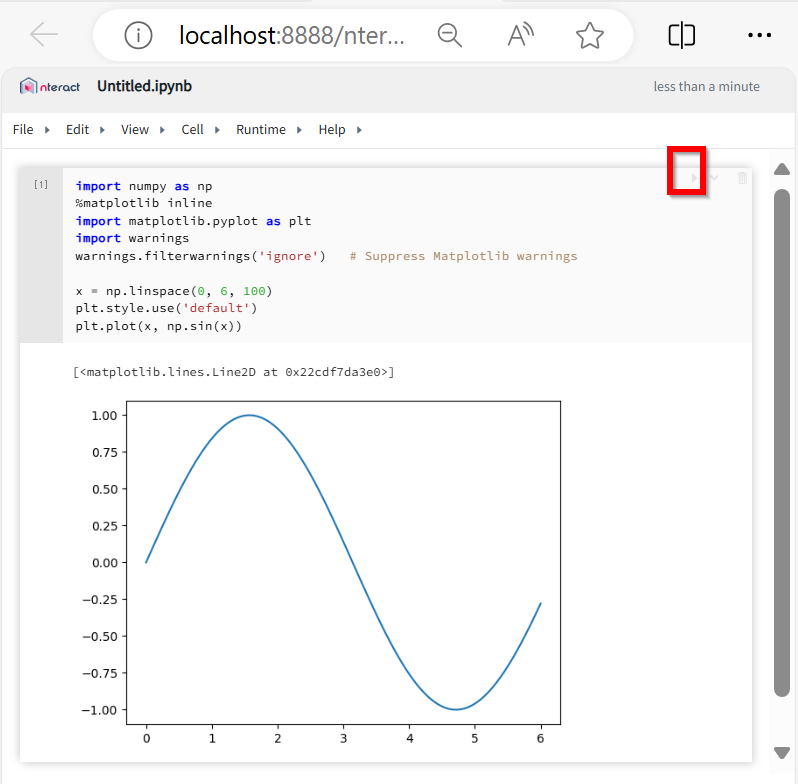
次のPythonプログラムを実行してみる。そのために「Start a new notebook」の下の「Python」をクリックし、次のプログラムを入れ実行する。
次のプログラムは、NumPyとMatplotlibを使用して、0から6までの範囲のsin関数のグラフを描画する。warningsモジュールを使用してMatplotlibの警告表示を抑制し、Matplotlibでは、デフォルトのスタイルを使用する。
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore') # Suppress Matplotlib warnings
x = np.linspace(0, 6, 100)
plt.style.use('default')
plt.plot(x, np.sin(x))
Jupyter Notebookの保存設定
Jupyter Notebookで、保存のときに、.pyファイルと.ipynbファイルが保存されるように設定する。(この設定を行わないときは.ipynbファイルのみが保存される)
- 次のコマンドで、設定ファイルを生成する
jupyter notebook --generate-config - jupyter/jupyter_notebook_config.pyを編集し、末尾に、次を追加する
c.NotebookApp.contents_manager_class = "jupytext.TextFileContentsManager"
6. (9) PyScripter
PyScripterはPythonプログラム作成に関する種々の機能を持ったソフトウェアである。
WindowsでのPyScripterのインストールは、別ページで説明している。
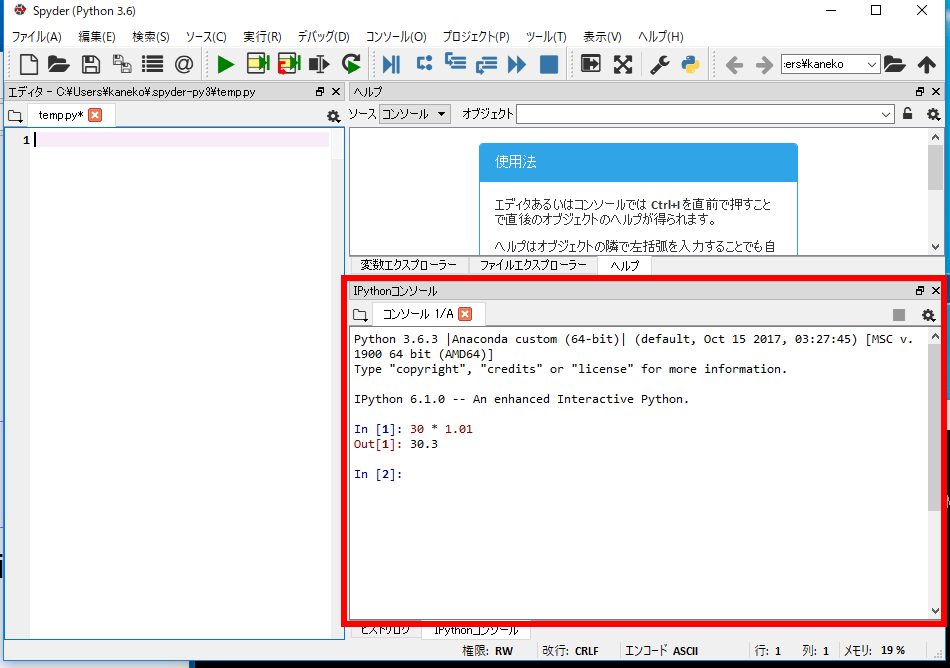
6. (10) spyder
Windowsで、Anaconda3をインストールしたときは、スタートメニューの「Anaconda3 (64-bit)」の下に「Spyder」があるので、これを使って実行するのが簡単である。
Ubuntuでは「spyder」で実行する。
spyderの右下の画面は、既定(デフォルト)で、Pythonコンソールになっている。
ラズベリーパイの場合は、次のコマンドでspyderをインストールすることができる。
sudo apt install python3-spyder
sudo apt install spyder3
6. (11) PyCharm
PyCharmはPythonプログラム作成に関する機能を持ったソフトウェアである。次の機能を持つ。
- Pythonプログラムの編集と実行
- Pythonコンソール
- Pythonの仮想環境
PyCharmでは、既定(デフォルト)でPythonの仮想環境が利用される。pipでPythonパッケージをインストールしたときなどで、システムのPythonを使いたいときは、別ページで説明する手順で設定する。
【PyCharm Community版の主な機能】
- 日本語言語パックのプラグイン
操作: Plugins、japaneseで検索、「Install」をクリック
- Pythonコードインスペクション
シンタックスハイライト、整形(コードフォーマッタ)、コード解析、修正候補の提示と実行(クイックフィックス)(Alt+Enterを使用)、コード補完など
- 検索
検索は、SHIFTを2回押す
- ビジュアルなデバッガ
ブレークポイント(マウスで指定可能)、変数値の表示など
https://www.jetbrains.com/ja-jp/pycharm/features/tools.html#debugger
- リファクタリング
名前の変更、メソッドの抽出など(メニューで実行可能)
- 型ヒント
型ヒントは、Alt+Enterを使用
https://www.jetbrains.com/help/pycharm/2016.3/type-hinting-in-pycharm.html
- 単体テストでpy.testを使うように設定
ファイル(File)、設定(Settings)、Python統合ツール(Python Integrated tools)、デフォルトのテストランナー(Default test runner)で、「pytest」を設定
Pythonプログラミングの基礎
7. (1) オブジェクトの生成と削除、同値、同一性
プログラミングでのオブジェクトは、コンピュータでの操作や処理の対象である。
キーワード: =、del、==、is
- 同値
a = 123 b = 123 print(a == b)
- 同一性
x = True y = None print(x is True) print(y is None)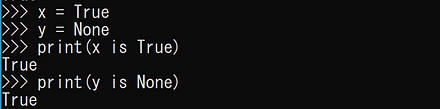
- オブジェクトの生成と削除
最後の「print(c)」の実行ではエラーメッセージが出る。
c = 123 print(c) del c print(c)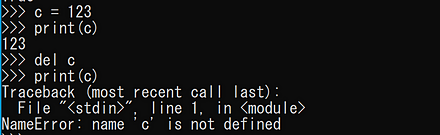
7. (2) 単純値のデータ型
- キーワード: int、float、Decimal、True、False、bool、None、str、bytes、list、range、tuple、dict、set
- int: 整数
- float: 浮動小数点数
- bool: ブール値
- str: 文字列
- bytes: バイト列
- 辞書(dictionary)
dic = {} dic.update( {"kaneko": 30} ) print(dic)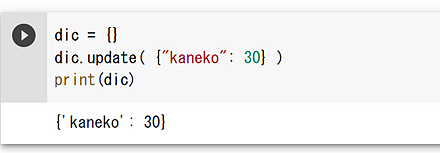
- 名前付きタプル(named tuple)
import collections Point3d = collections.namedtuple('Point3d', 'x y z') p = Point3d(10, 20, 30) print(p)
7. (3) オブジェクトのタイプ
print( type(100) )
print( type(1.23) )
print( type(True) )
print( type(False) )
print( type("Hello") )
print( type([1, 2, 3]) )
dic = {}
dic.update( {"kaneko": 30} )
print( type(dic) )
import collections
Point3d = collections.namedtuple('Point3d', 'x y z')
p = Point3d(10, 20, 30)
print( type(p) )
import numpy as np
print( type(np.zeros(10)) )
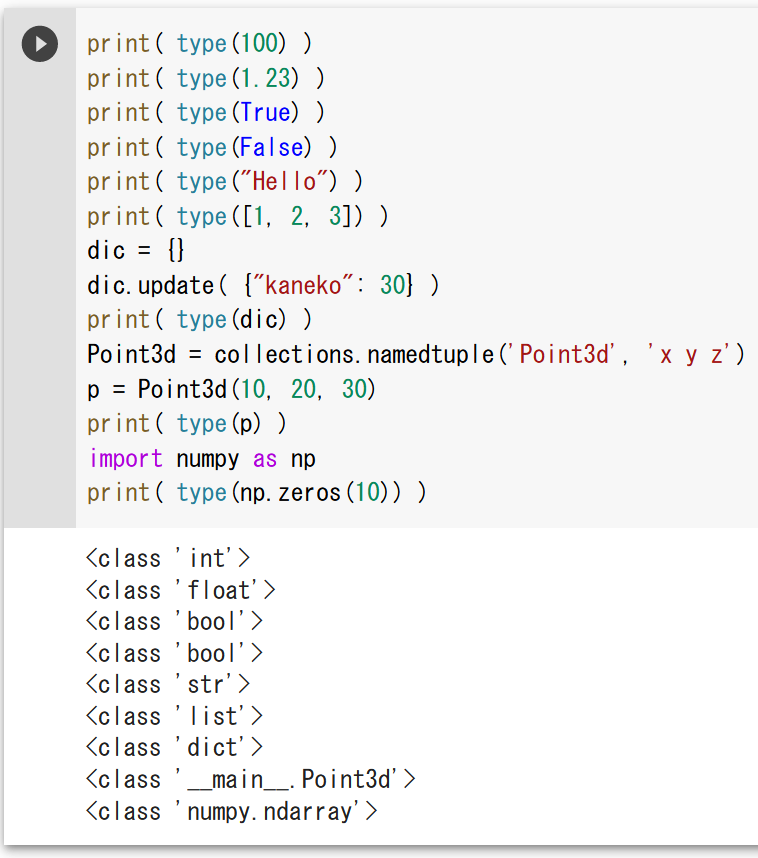
制御構造(条件分岐、繰り返し)
キーワード: if、elif、else、while、break、for
条件分岐
- 条件分岐
変数の値によって、実行の流れが変わる。
age = 15 if (age <= 12): print(500) else: print(1800)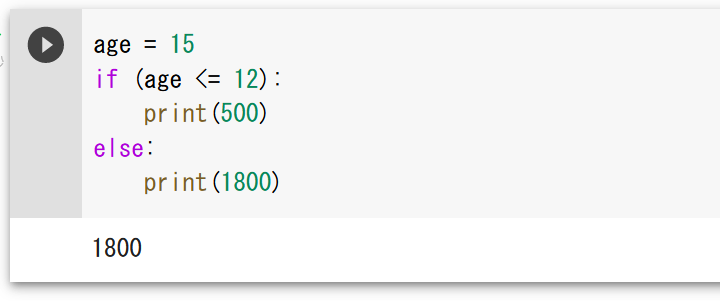
- 多分岐
age = 15 if age <= 12: print(500) elif age <= 15: print(1000) else: print(1800)
繰り返し
- whileによる繰り返し
b = 8 s = 0 while s < 100: s = s + b print(s)
- forによる繰り返し
for i in range(10): print(i)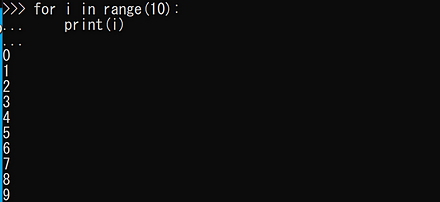
- 月の日数
月の日数についてのデータを作る。うるう年は考慮しない。
import numpy as np days = np.array([0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]) print( days[7] ) print( days[9] )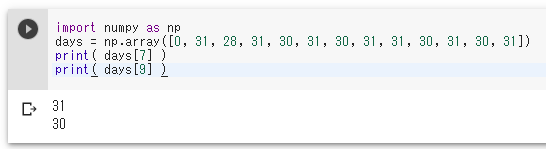
- 物体の落下
import numpy as np x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) for t in x: print( (9.8 / 2) * t * t )
- 10倍
import numpy as np x = np.array([8, 6, 4, 2, 3]) y = np.array([0, 0, 0, 0, 0]) for i in range(0,5): y[i] = x[i] * 10 print(x) print(y)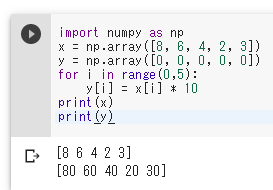
- 「*」の表示を18回繰り返す
import sys for i in range(18): sys.stdout.write("*")
文字列の演算子
キーワード: +、in、%、split、join、replace、strip、match、sprintf
pandasデータフレーム
Pandasを用いたデータの扱い(CSVファイル読み込み、散布図、要約統計量、ヒストグラム)を示す。
説明のために、次のCSVファイルを使う。ファイル名はenquete.csvである。
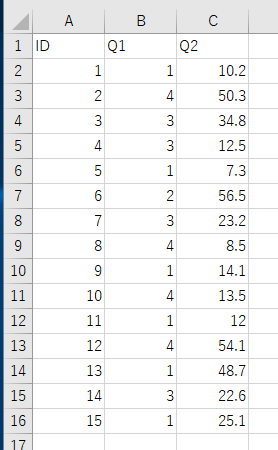
このCSVファイルのダウンロードは、Windowsでコマンドプロンプトを管理者として開き、次のコマンドを実行する。
cd C:\
curl -O https://www.kkaneko.jp/sample/csv/enquete.csv
上のコマンドが実行できないときは、次のリンクからダウンロードする。ダウンロードしたファイルは、C:\の直下に置く。 https://www.kkaneko.jp/sample/csv/enquete.csv
CSVファイルの読み込み、確認
Pythonでグラフや図を表示する場合、Windowsでは、スタートメニューの「IDLE(Python ...)」、spyder3コマンド、PyCharmが便利である。
- アンケートデータの読み込み
import pandas as pd import seaborn as sns x = pd.read_csv('C:/enquete.csv', encoding='SHIFT-JIS')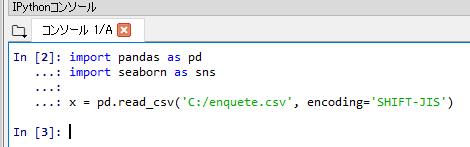
先頭行にデータ本体がある(先頭行が属性名でない)ときは、「pd.read_csv('hoge.csv', header=None)」のようにする。
- 読み込んだデータの表示
print(x)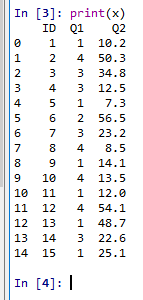
- 読み込んだデータのうち、1列目と2列目の表示
オブジェクトxには0列目と1列目と2列目がある。
print(x.iloc[:,1]) print(x.iloc[:,2])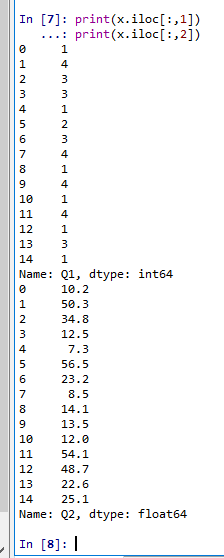
- 読み込んだデータについて、1列目と2列目の散布図
「plt.style.use('ggplot')」はグラフの書式の設定である。「ro」は赤い丸を意味する。
%matplotlib inline import matplotlib.pyplot as plt import warnings warnings.filterwarnings('ignore') plt.style.use('ggplot') plt.plot(x.iloc[:,1], x.iloc[:,2], 'ro') plt.show()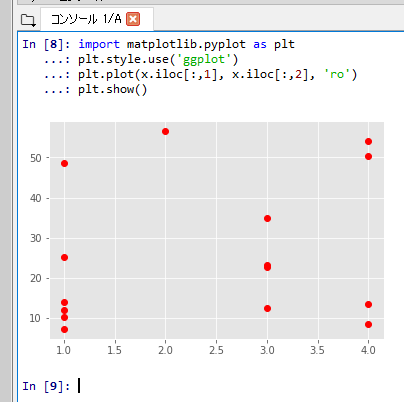
- 各列について、基本的な情報の表示
- head: 先頭部分の表示
- shape: サイズ
- ndim: 次元数
- columns: 属性名
- info(): 各属性のデータ型
print(x.head()) print(x.info()) print(x.shape) print(x.ndim) print(x.columns)
- CSVファイルに書き出し
x.to_csv('hoge.csv', header=True, index=False, encoding='SHIFT-JIS')
各属性の要約統計量
総数、平均、標準偏差、最小、四分位点、中央値、最大を表示する。
print(x.describe())

JSONファイルの書き出しと読み込み
import pandas as pd
x.to_json('hoge.json')
a = pd.read_json('hoge.json')
pandas.DataFrameのコンストラクタ
- リストから
import pandas as pd pd.DataFrame([1, 2, 3]) - numpy.ndarrayから
import numpy as np import pandas as pd pd.DataFrame( np.array([1,2,3]) )import numpy as np import pandas as pd pd.DataFrame( np.array([[1,2,3], [10,20,30], [100,200,300]]) ) - 辞書から
import pandas as pd pd.DataFrame( {'x' : [1, 2, 3], 'y' : [4, 5, 6]} )
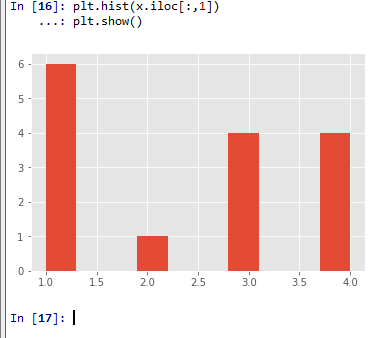
ヒストグラムの表示
import matplotlib.pyplot as plt
plt.hist(x.iloc[:,1])
plt.show()
plt.hist(x.iloc[:,2])
plt.show()
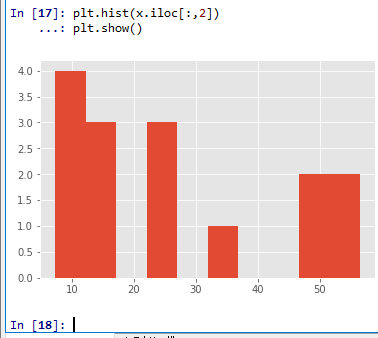
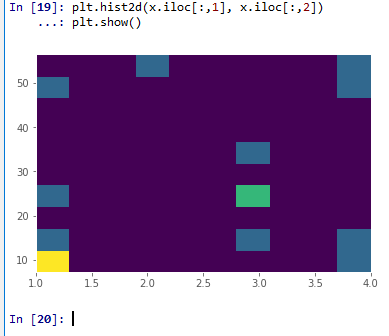
2次元ヒストグラム
import matplotlib.pyplot as plt
plt.hist2d(x.iloc[:,1], x.iloc[:,2])
plt.show()
numpy全般
次元数
numpyの1次元の配列の次元数は1である(ndimで得る)。
1次元の配列の形は(<要素数>,)のように表示される(shapeで得る)。
import numpy as np
x = np.zeros(10)
print( x.ndim )
print( x.shape )

numpyの2次元の配列の次元数は2である(ndimで得る)。
2次元の配列の形は(<要素数>,<要素数>)のように表示される(shapeで得る)。
import numpy as np
x = np.zeros((2, 3))
print( x.ndim )
print( x.shape )

データ型と、要素のデータ型
1次元の配列のデータ型はnumpy.ndarrayである(typeで得る)。
配列の要素のデータ型はdtypeを使って表示する。「float64」は浮動小数点数である。
import numpy as np
x = np.zeros(10)
print( type( x ) )
print( x.dtype )

2次元の配列のデータ型はnumpy.ndarrayである(typeで得る)。
配列の要素のデータ型はdtypeを使って表示する。「float64」は浮動小数点数である。
import numpy as np
x = np.zeros((2, 3))
print( type( x ) )
print( x.dtype )

1次元の配列
配列は、データの並びで、それぞれのデータに、0から始まる番号(添字)が付いている。
1次元の配列の生成
- 0要素
typeはオブジェクトのタイプの取得である。shapeは配列のサイズの取得である。
import numpy as np x = np.zeros(10) print(x) print(type(x)) print(x.shape)表示の「0.」は「0」を意味する。
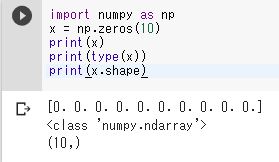
- 1要素
import numpy as np x = np.ones(10) print(x) print(type(x)) print(x.shape)表示の「1.」は「1」を意味する。
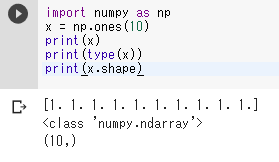
- 乱数(正規分布、平均が0)
import numpy as np x = np.random.randn(10) print(x) print(type(x)) print(x.shape)
- 要素指定
import numpy as np x = np.array([3, 1, 2, 5, 4]) print(x) print(type(x)) print(x.shape)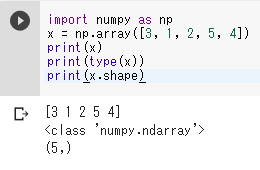
- arangeによる指定
-5から開始して、2ずつ増やし、4まで
import numpy as np x = np.arange(-5, 4, 2) print(x) print(type(x)) print(x.shape)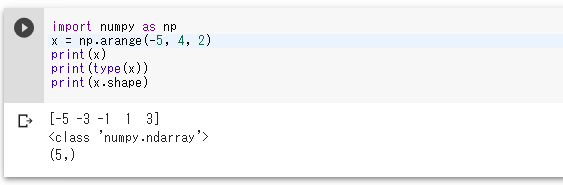
- linspaceによる指定
-2から、2まで、全部で、9個
import numpy as np x = np.linspace(-2, 2, 9) print(x) print(type(x)) print(x.shape)
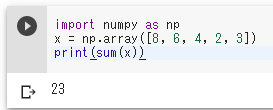
合計
import numpy as np
x = np.array([8, 6, 4, 2, 3])
print(sum(x))
2次元の配列
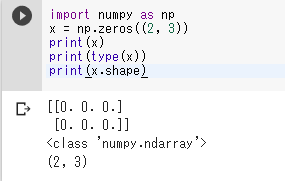
import numpy as np
x = np.zeros((2, 3))
print(x)
print(type(x))
print(x.shape)
表示の「0.」は「0」を意味する。
import numpy as np
x = np.ones((2, 3))
print(x)
print(type(x))
print(x.shape)
表示の「1.」は「1」を意味する。

import numpy as np
x = np.random.randn(2,3)
print(x)
print(type(x))
print(x.shape)
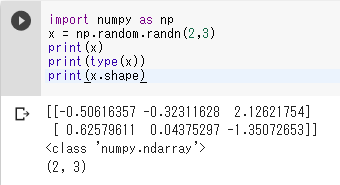
- 乱数(正規分布)
import numpy as np x = np.random.randn(2,3) print(x)
2次元の配列の処理
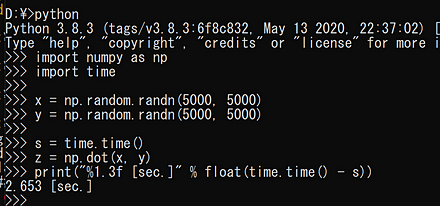
行列の積
時間計測も行う。
import numpy as np
import time
x = np.random.randn(5000, 5000)
y = np.random.randn(5000, 5000)
s = time.time()
z = np.dot(x, y)
print("%1.3f [sec.]" % float(time.time() - s))
CuPyを用いて行列の積を求める
時間計測も行う。
- CPUを用いて、行列の積を求める
!pip3 install cupy import numpy as np use_gpu=False if use_gpu: import cupy npcp = cupy else: npcp = np x = npcp.random.random((5000, 5000)) y = npcp.random.random((5000, 5000)) import datetime a = datetime.datetime.now() npcp.dot(x, y) print( (a - datetime.datetime.now()).microseconds )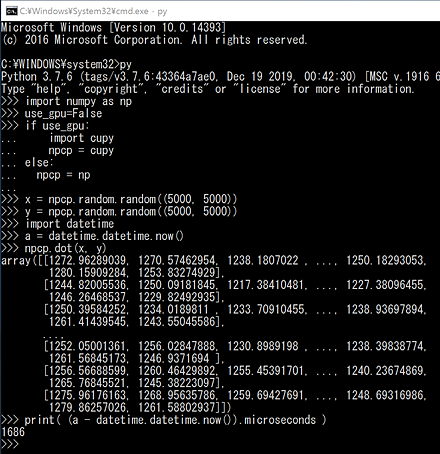
- GPUを用いて、行列の積を求める
上のプログラムで、「use_gpu=False」を「use_gpu=True」に変更する。
!pip3 install cupy import numpy as np use_gpu=True if use_gpu: import cupy npcp = cupy else: npcp = np x = npcp.random.random((5000, 5000)) y = npcp.random.random((5000, 5000)) import datetime a = datetime.datetime.now() npcp.dot(x, y) print( (a - datetime.datetime.now()).microseconds )
行列の積、主成分分析、SVD、k-means
次のプログラムは、NumPyとscikit-learnを使用して、行列計算とデータ分析を行う。
- 2000x2000の乱数行列XとYを生成し、それらの行列積を計算する。
- scikit-learnのPCAを使用して、Xの主成分分析を行い、2次元に次元削減する。
- NumPyのsvd関数を使用して、Xの特異値分解を行う。
- scikit-learnのKMeansを使用して、Xに対して10クラスタのk-meansクラスタリングを行う。
各操作の実行時間を測定し、結果を出力する。
import time
import numpy
import numpy.linalg
import sklearn.decomposition
import sklearn.cluster
X = numpy.random.rand(2000, 2000)
Y = numpy.random.rand(2000, 2000)
# 行列の積
a = time.time(); Z = numpy.dot(X, Y); print(time.time() - a)
# 主成分分析
pca = sklearn.decomposition.PCA(n_components = 2)
a = time.time(); pca.fit(X); X_pca = pca.transform(X); print(time.time() - a)
# SVD
a = time.time(); U, S, V = numpy.linalg.svd(X); print(time.time() - a)
# k-means
a = time.time();
kmeans_model = sklearn.cluster.KMeans(n_clusters=10, random_state=10).fit(X)
labels = kmeans_model.labels_
print(time.time() - a)
numpyのnpz形式ファイルの書き出しと読み込み
import numpy as np
np.savez('hoge.npz',a = np.array([1, 2, 3]), b = np.array([1, 2, 3]))
m = np.load('hoge.npz')
print( m['a'] )
print( m['b'] )
2次元配列データのCSVファイル読み書き
CSVファイルへの書き出しはpandasの機能で行う。次のプログラムを実行すると、ファイルXX.csvとYY.csvが作成される。
import numpy as np
import pandas as pd
X, Y = np.meshgrid( np.array([2, 3, 4]), np.array([10, 20]) )
XX = pd.DataFrame(X)
print(XX)
XX.to_csv("XX.csv", header=False, index=False)
YY = pd.DataFrame(Y)
print(YY)
YY.to_csv("YY.csv", header=False, index=False)
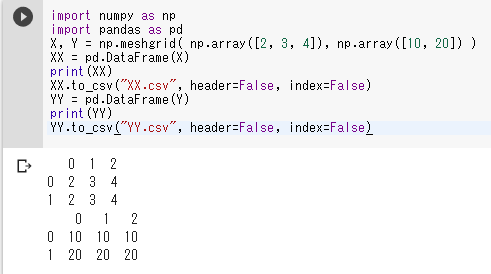
CSVファイルの読み込みもpandasの機能で行う。次のプログラムは、作成したファイルXX.csvを読み込む。
pd.read_csv("XX.csv", header=None)
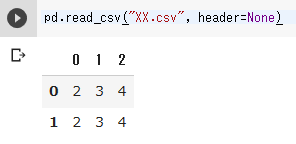
同様に、ファイルYY.csvを読み込む。
pd.read_csv("YY.csv", header=None)

メッシュグリッド
メッシュグリッドは、3次元グラフの作成や繰り返し計算を行う際に使用する。
import numpy as np
X, Y = np.meshgrid( np.array([2, 3, 4]), np.array([10, 20]) )
print(X)
print(type(X))
print(X.shape)
print(Y)
print(type(Y))
print(Y.shape)

配列の次元を増やす
1次元配列を2次元配列に変換する。次のプログラムは、1次元配列xを2次元配列AとBに変換する。
import numpy as np
x = np.array([3, 1, 2, 5, 4])
A = x[:, np.newaxis]
B = x[np.newaxis, :]
print(A)
print(type(A))
print(A.shape)
print(B)
print(type(B))
print(B.shape)
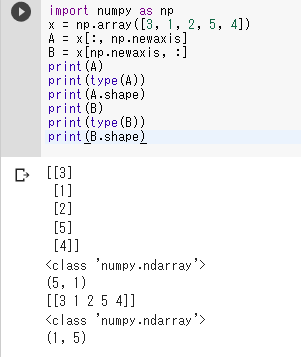
リスト
Pythonのリストは、複数の要素を格納できるデータ構造である。
a = [1, 2, 3, 4]
print(a)
type(a)

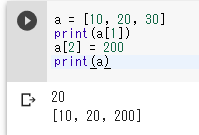
Pythonのリストの添字は0から開始する。
a = [10, 20, 30]
print(a[1])
a[2] = 200
print(a)
Pythonのモジュール
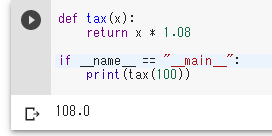
Pythonのモジュールは、1つ以上の関数を集めて1つのファイルにまとめたものである。次のモジュールには関数taxが含まれている。
Pythonのモジュールは単体でも実行できるように作成できる。これはモジュールのテストを行う際に有用である(「if __name__ == "__main__"」から始まる部分が、単体実行を可能にする記述である)。
def tax(x):
return x * 1.08
if __name__ == "__main__":
print(tax(100))
このモジュールを他のプログラムでインポートして使用する場合は、モジュールを「hoge.py」のようなファイル名で保存する。その後、プログラムを次のように記述する。
import hoge
print(hoge.tax(10))
Pythonのライブラリ
Pythonには様々な機能を提供するライブラリが用意されている。
現在の日時
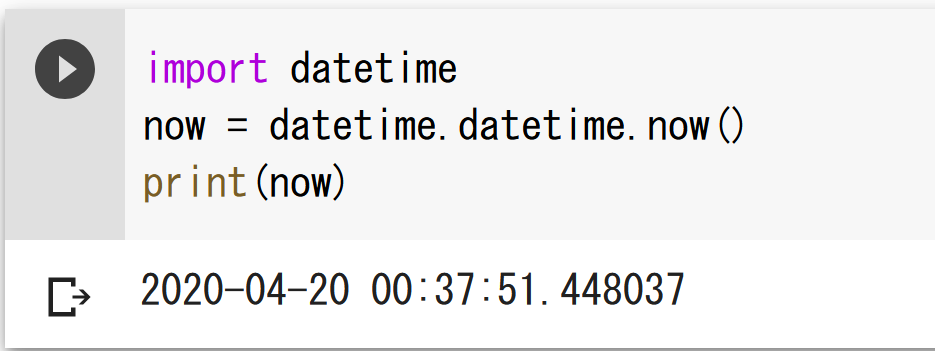
オペレーティングシステムのタイマーを利用して、現在の日時を取得できる。
import datetime
now = datetime.datetime.now()
print(now)
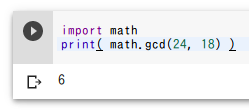
最大公約数
24と18の最大公約数を求める。
import math
print( math.gcd(24, 18) )
方程式を解く
方程式4x + 1 = 0を解く。
from scipy import optimize
def foo(x):
return 4 * x + 1
print( optimize.fsolve(foo, 10) )
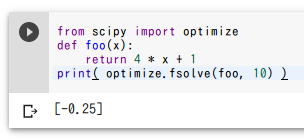
平方根
面積が7の正方形の一辺の長さを求める。
import math
print( math.sqrt(7) )
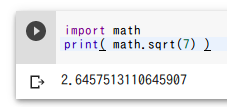
円の面積
半径3の円の面積を求める。円周率にはmath.piを使用する。
import math
print( 3 * 3 * math.pi )
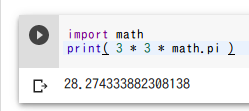
三角形の面積
2辺の長さが4と6で、その間の角度が60度の三角形の面積を求める。
import math
print( (1/2) * 4 * 6 * math.sin(60 * math.pi / 180) )
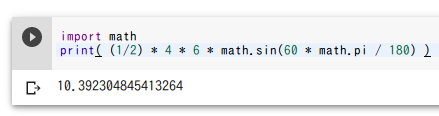
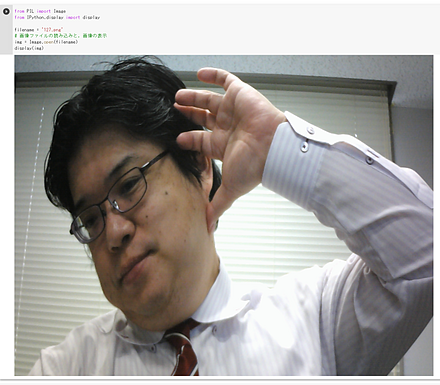
IPython.displayを用いた画像表示
画像ファイルを読み込んで表示する。
from PIL import Image
from IPython.display import display
filename = '127.png'
img = Image.open(filename)
display(img)
Matplotlibを用いた散布図のプロット
matplotlibは、オープンソースのPythonプロットライブラリである。
- リストx、yからの散布図の作成
%matplotlib inline import matplotlib.pyplot as plt import warnings warnings.filterwarnings('ignore') import numpy as np x = [1, 2, 3, 4, 5] y = [2, 4, 1, 3, 5] plt.style.use('ggplot') plt.scatter(x, y)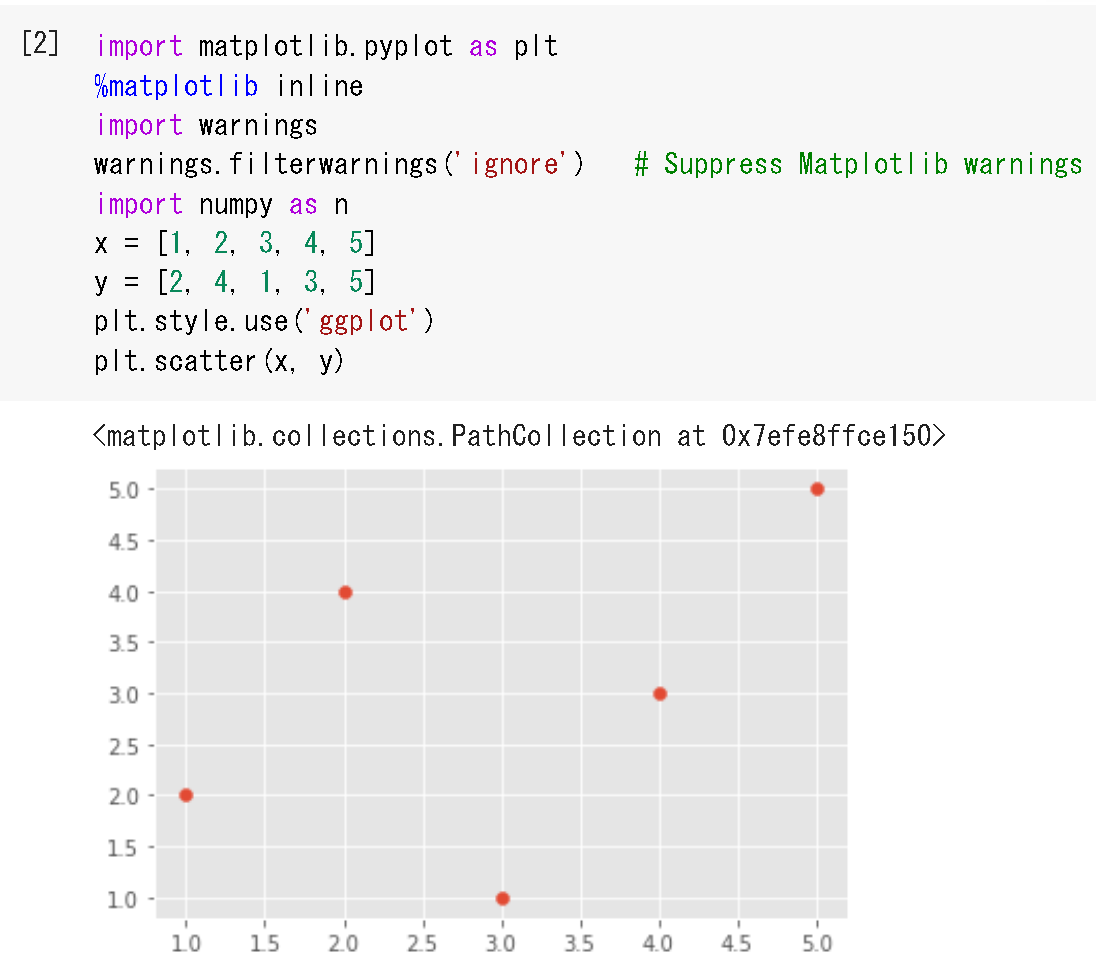
- pandasのDataFrameの2つの属性x、yからの散布図の作成
import numpy as np import pandas as pd %matplotlib inline import matplotlib.pyplot as plt import warnings warnings.filterwarnings('ignore') a = pd.DataFrame( {'x' : [1, 2, 3, 4, 5], 'y' : [2, 4, 1, 3, 5]} ) plt.style.use('ggplot') plt.plot(a['x'], a['y'], 'ro') plt.show()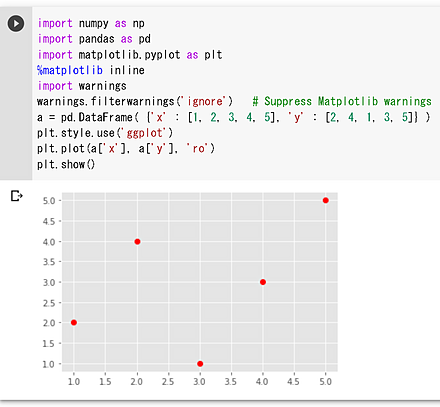
3次元散布図
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
import numpy as np
from mpl_toolkits.mplot3d import axes3d
plt.style.use('ggplot')
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
x = [1, 2, 3, 4, 5]
y = [2, 4, 1, 3, 5]
z = [1, 1, 2, 2, 3]
ax.scatter(x, y, z, c='b')
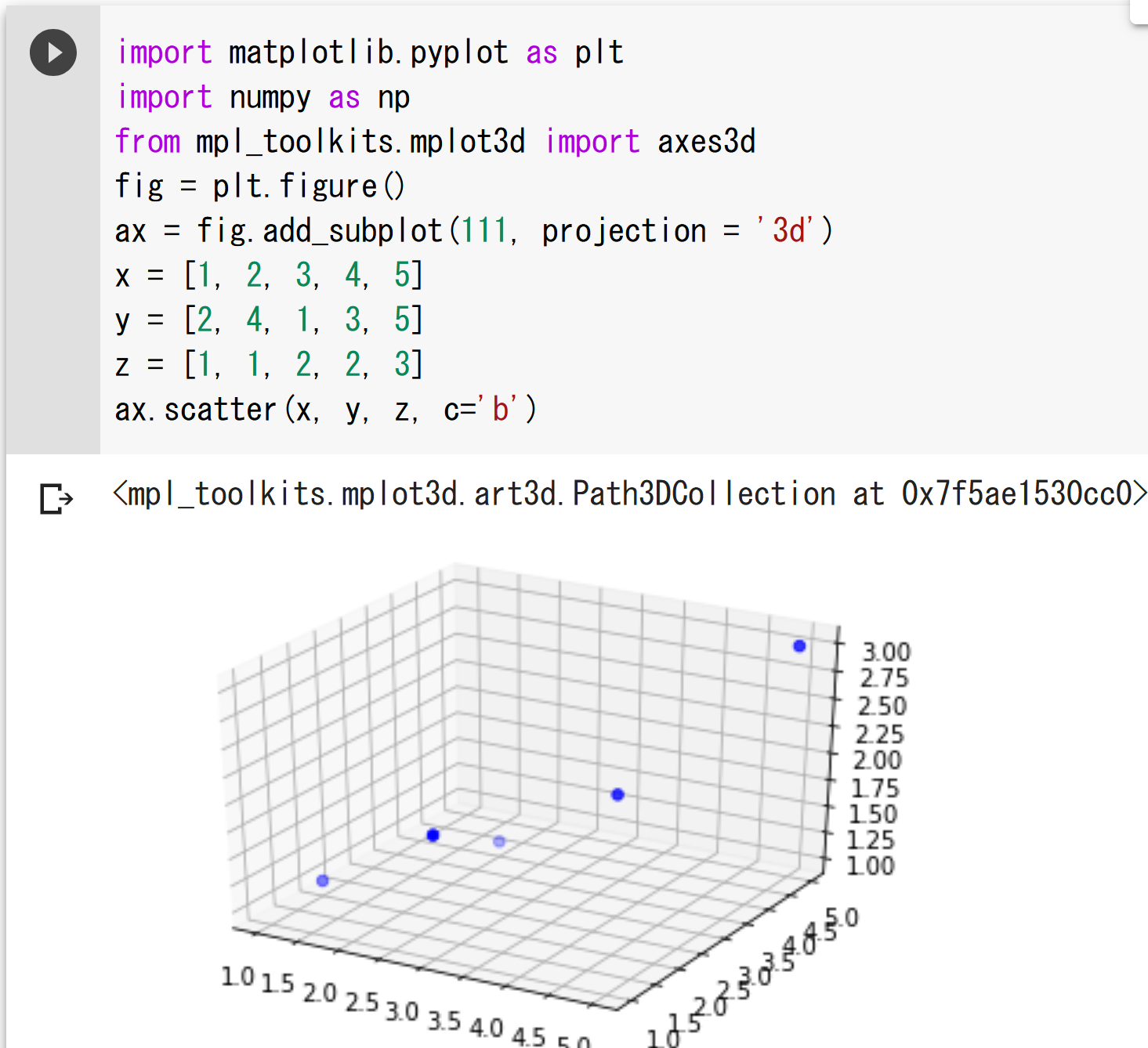
Matplotlibを用いた種々のプロット
OpenCV画像の表示
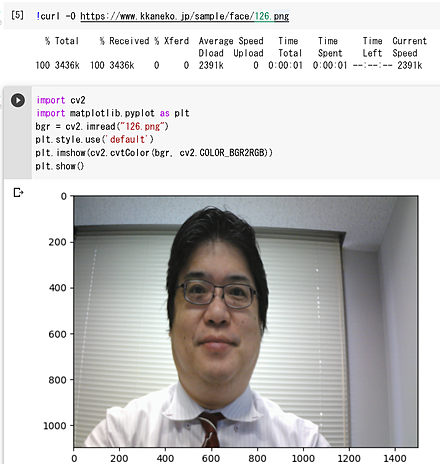
matplotlibを用いてOpenCVのカラー画像を表示する。
import cv2
import matplotlib.pyplot as plt
bgr = cv2.imread("126.png")
plt.style.use('default')
plt.imshow(cv2.cvtColor(bgr, cv2.COLOR_BGR2RGB))
plt.show()
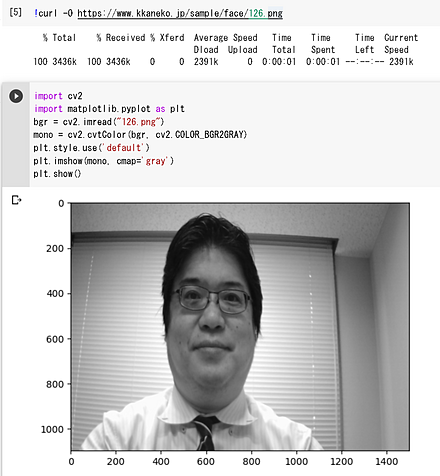
matplotlibを用いてOpenCVの濃淡画像を表示する。
import cv2
import matplotlib.pyplot as plt
bgr = cv2.imread("126.png")
mono = cv2.cvtColor(bgr, cv2.COLOR_BGR2GRAY)
plt.style.use('default')
plt.imshow(mono, cmap='gray')
plt.show()
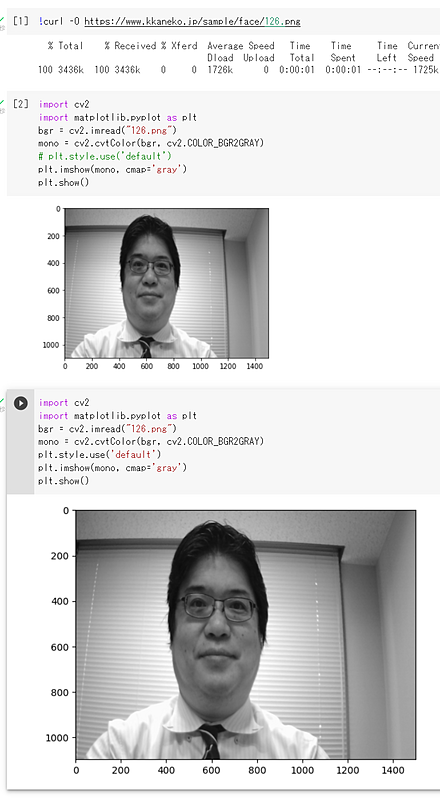
Matplotlibでのサイズ調整
MatplotlibでOpenCV画像を表示すると、デフォルトでは小さく表示される場合がある。「plt.style.use('default')」を実行することで、表示サイズを大きくできる。
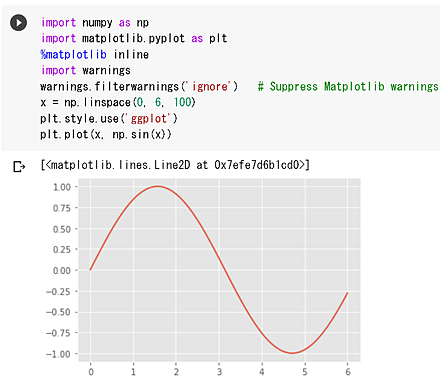
関数のプロット
matplotlibを用いたグラフ描画の例を示す。
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
x = np.linspace(0, 6, 100)
plt.style.use('ggplot')
plt.plot(x, np.sin(x))
メッシュグリッドと関数の3次元プロット
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
import numpy as np
from mpl_toolkits.mplot3d import axes3d
plt.style.use('ggplot')
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
X, Y = np.meshgrid( np.array([-2, -1, 0, 1, 2]), np.array([-3, -2, -1, 0, 1, 2, 3]) )
def f(x,y):
return x * y
Z = f(X, Y)
ax.scatter(X, Y, Z, c='b')
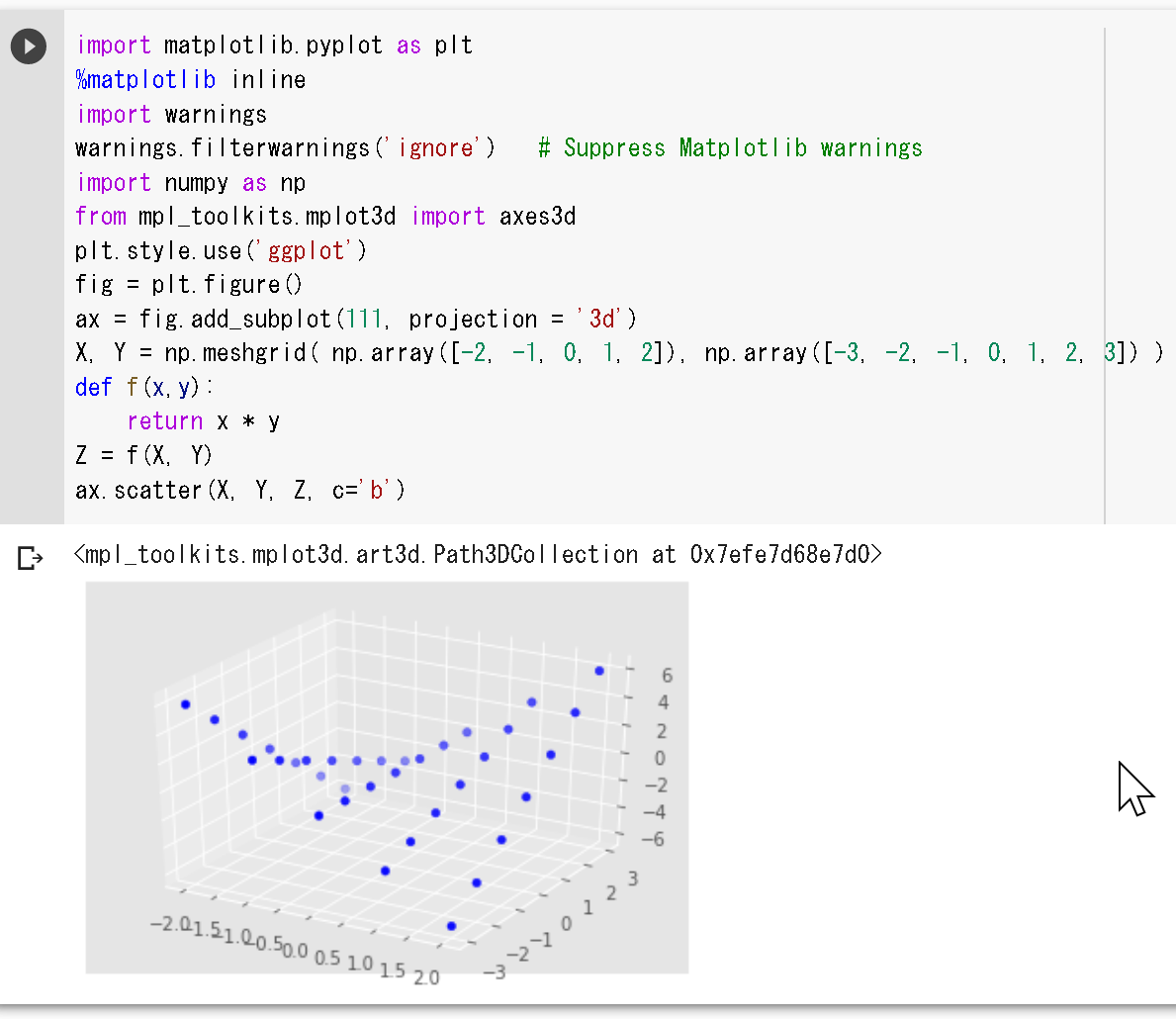
x1、x2のソフトマックス関数の3次元プロット。
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
import numpy as np
from mpl_toolkits.mplot3d import axes3d
plt.style.use('ggplot')
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
X1, X2 = np.meshgrid( np.array([-2, -1, 0, 1, 2]), np.array([-3, -2, -1, 0, 1, 2, 3]) )
def softmax(x):
A = np.exp(x - np.max(x))
return A / A.sum()
def f(x1, x2):
return softmax( np.array([x1, x2]) )
Z = f(X1, X2)
ax.scatter(X1, X2, Z[0], c='b')
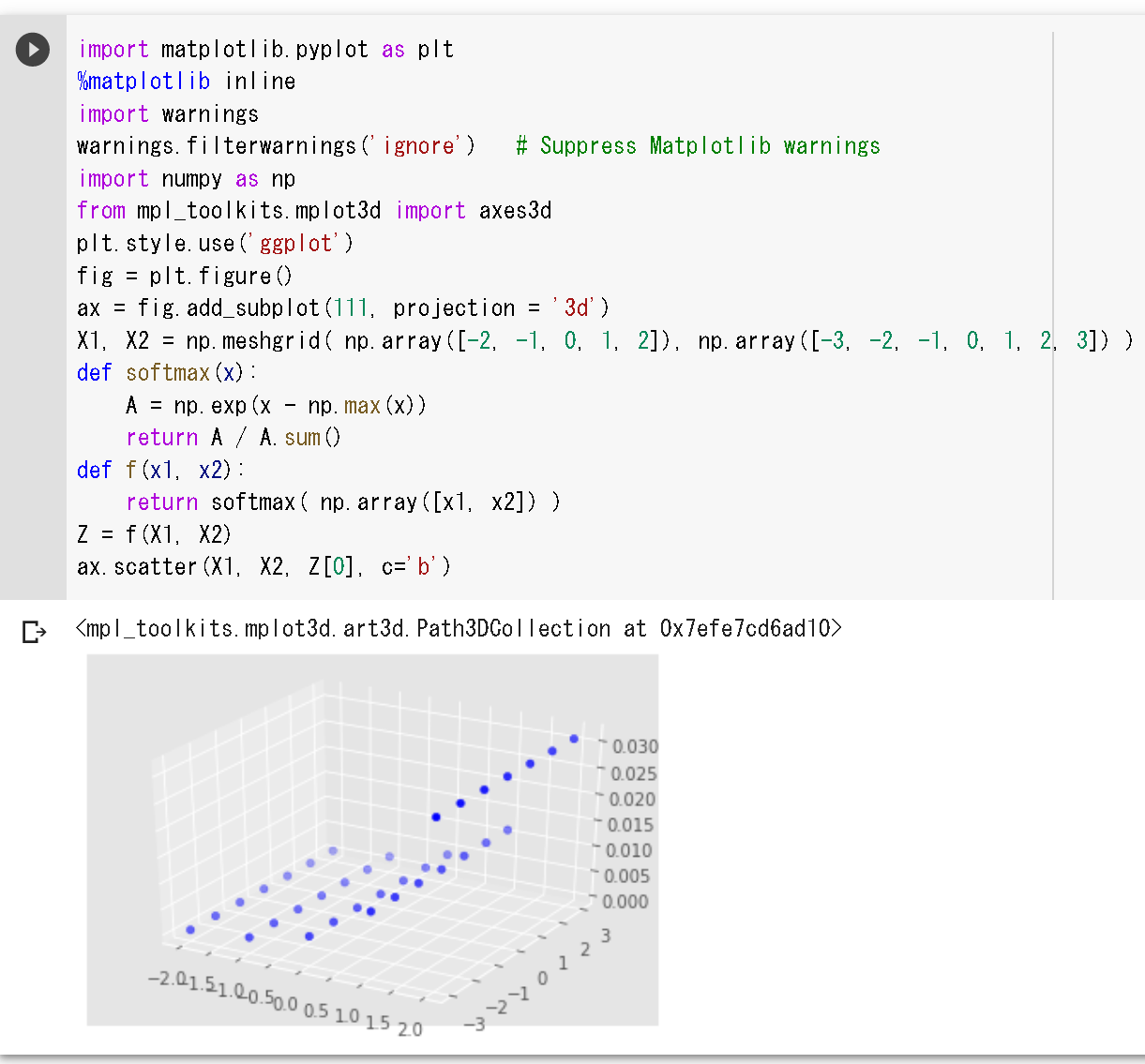
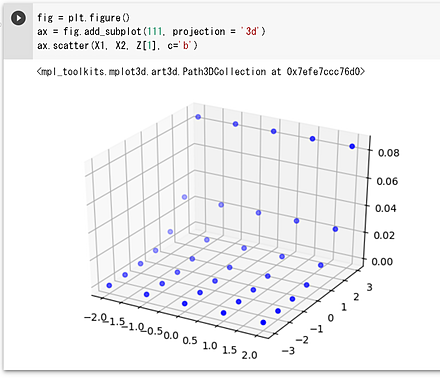
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
ax.scatter(X1, X2, Z[1], c='b')
TensorFlow
TensorFlowは、Googleが開発した機械学習フレームワークである。Python、C/C++言語から利用可能で、CPU、GPU、TPU上で動作する。TensorFlowの特徴として「データフローグラフ」がある。これは、データの流れを表現するもので、グラフの節点は演算を、エッジはデータ(テンソル)の流れを表す。TensorFlowを使用することで、音声、画像、テキスト、ビデオなど多様なデータを扱う機械学習アプリケーションの開発が容易になる。
TensorFlowのプログラム例として、行列の足し算を示す。
import tensorflow as tf
import numpy as np
a = tf.constant( np.reshape([1, 1, 1, 1, 1, 1], (2, 3) ) )
b = tf.constant( np.reshape( [1, 2, 3, 4, 5, 6], (2, 3) ) )
c = tf.add(a, b)
print(c)

Keras
Kerasは、TensorFlowを用いてディープラーニング(深層学習)でのモデルの構築と訓練を簡単に行えるようにするソフトウェアである。
用語集
- Kerasのモデルは、複数の層が組み合わさったものである。単純に層を積み重ねたもの(シーケンシャル)や、複雑な構成のもの(グラフ)がある。
- Kerasの層には、活性化関数、層の重みの種類(カーネル、バイアスなど)を設定できる。
- Kerasの層には、全結合、畳み込み(コンボリューション)などの種類がある。
- 学習のために、オプティマイザの設定を行う。
- Kerasのモデルの構成やオプティマイザの設定は保存できる。
- 学習の結果は結合の重みになる。結合の重みも保存できる。
ニューラルネットワークのデモサイト: http://playground.tensorflow.org
手順
-
パッケージのインポート
from __future__ import absolute_import, division, print_function, unicode_literals import tensorflow as tf import tensorflow_datasets as tfds from tensorflow import keras import numpy as np %matplotlib inline import matplotlib.pyplot as plt import warnings warnings.filterwarnings('ignore') print(tf.__version__)
- 画像データセットMNISTの準備
x_train: サイズ28×28の60000枚の濃淡画像
y_train: 60000枚の濃淡画像それぞれの種類番号(0から9のどれか)
x_test: サイズ28×28の10000枚の濃淡画像
y_test: 10000枚の濃淡画像それぞれの種類番号(0から9のどれか)
mnist, metadata = tfds.load( name="mnist", as_supervised=False, with_info=True, batch_size = -1) train, test = mnist['train'], mnist['test'] print(metadata) x_train, y_train = train["image"].numpy().astype("float32") / 255.0, train["label"] x_test, y_test = test["image"].numpy().astype("float32") / 255.0, test["label"]
- 画像データセットMNISTの確認表示
plt.style.use('default') plt.figure(figsize=(10,10)) for i in range(25): plt.subplot(5,5,i+1) plt.xticks([]) plt.yticks([]) plt.grid(False) image, label = train["image"][i], train["label"][i] plt.imshow(image.numpy()[:, :, 0].astype(np.float32), cmap='gray') plt.xlabel(label.numpy()) plt.show()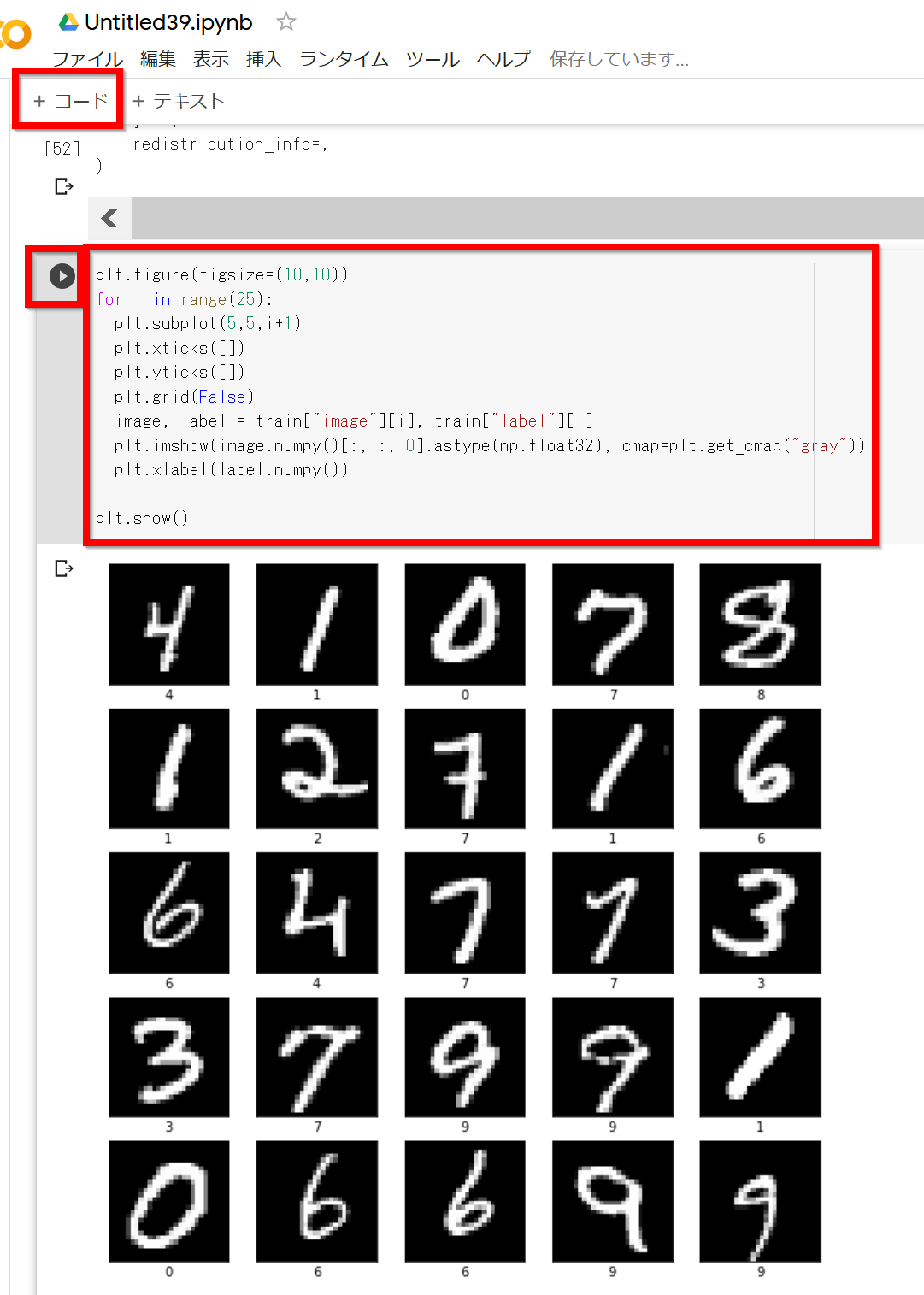
- 配列の形状と次元の確認
配列の形: 60000×28×28
次元: 3
print( x_train.shape ) print( x_train.ndim )
- ディープニューラルネットワークのモデルの作成
2層のニューラルネットワークを作成する。1層目のユニット数は128、2層目のユニット数は10である。
m = tf.keras.Sequential() m.add(tf.keras.layers.Flatten(input_shape=(28, 28, 1))) m.add(tf.keras.layers.Dense(units=128, activation='relu')) m.add(tf.keras.layers.Dropout(rate=0.2)) m.add(tf.keras.layers.Dense(units=10, activation='softmax')) m.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.001), loss='sparse_categorical_crossentropy', metrics=['accuracy'])
- ニューラルネットワークの確認表示
print(m.summary())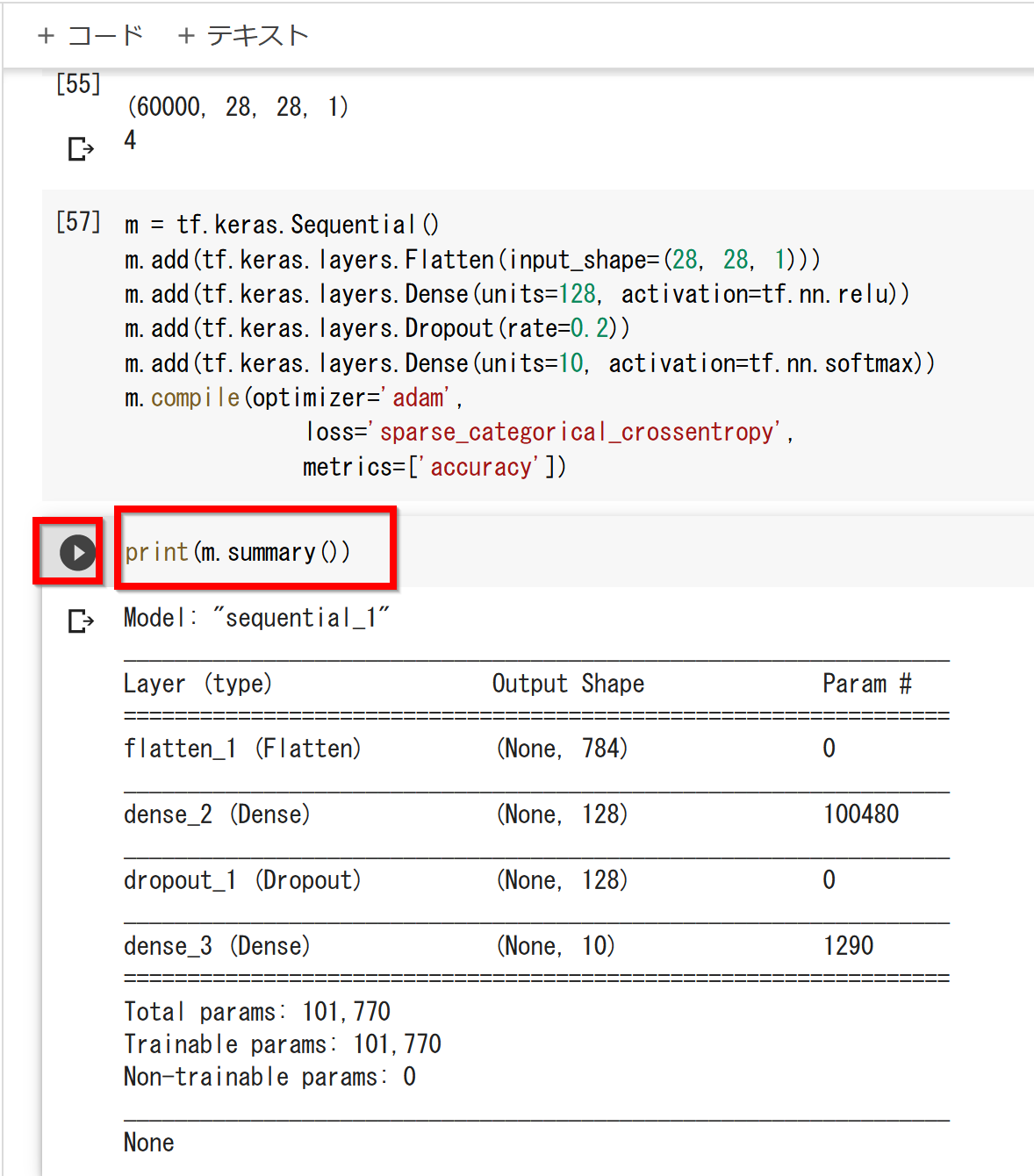
- ニューラルネットワークの学習を行う
history = m.fit(x_train, y_train, epochs=50)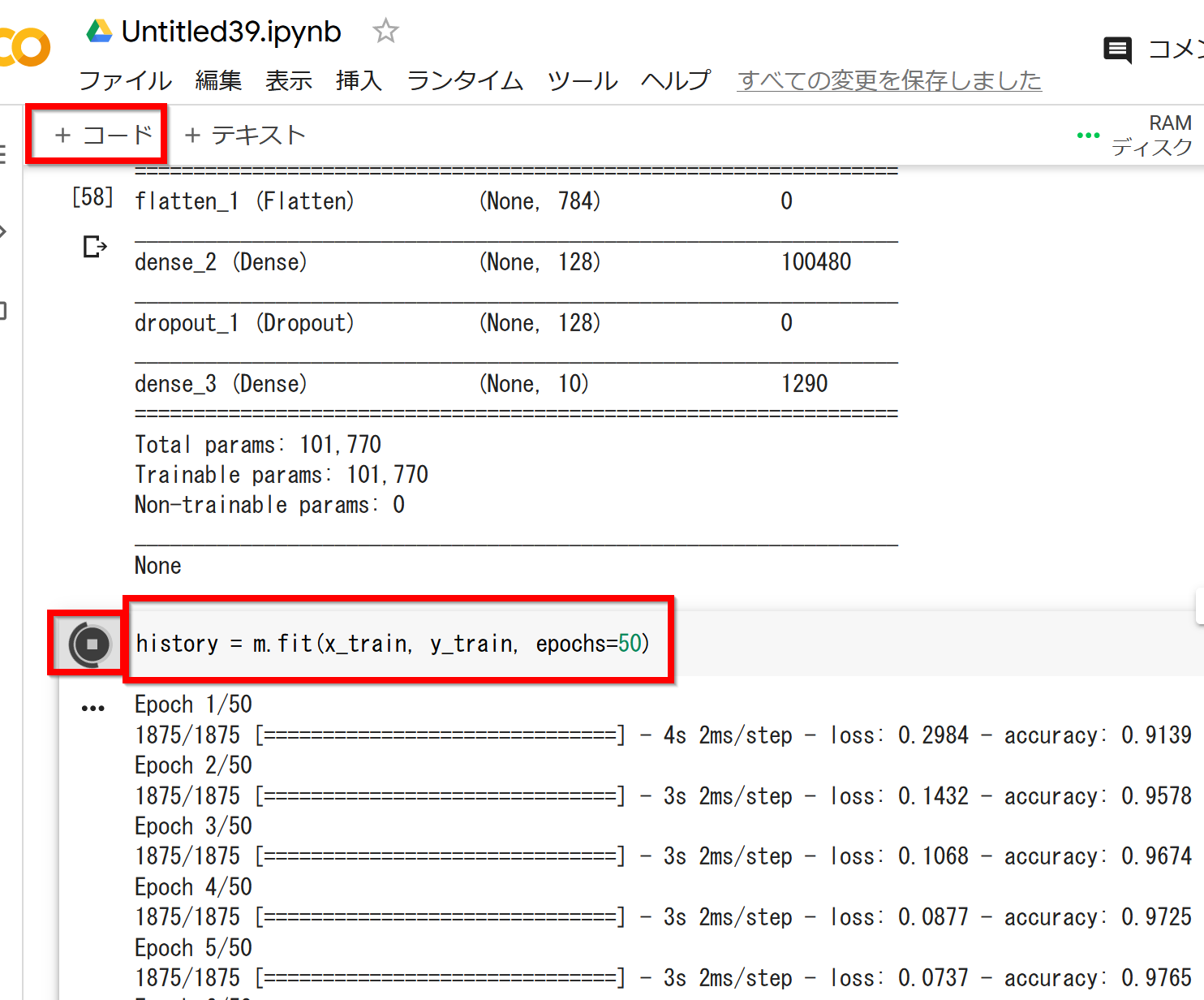
- 検証用データで検証する
print( m.evaluate(x_test, y_test, verbose=2) )訓練(学習)などで乱数が使われるため、実行ごとに結果が異なる場合がある。
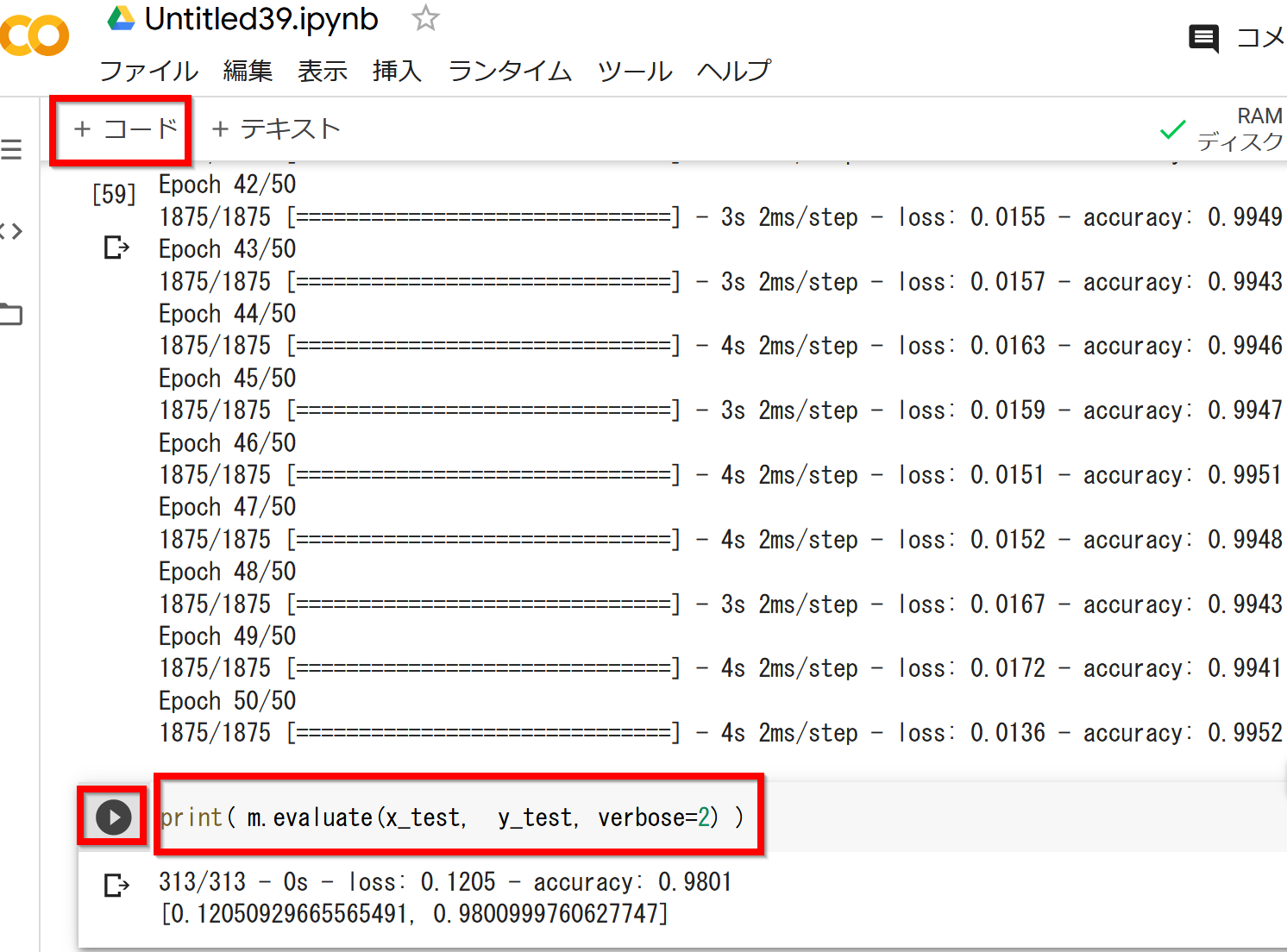
- ニューラルネットワークを使ってみる
テスト画像をニューラルネットワークに与えて予測させる。テスト画像は0から9の数字が書かれた画像である。
predictions = m.predict(x_test) print(predictions[0])結果の見方: 0である確率、1である確率、2である確率、...、9である確率と、10個の数字が結果として得られる。先ほど作成したニューラルネットワークの2層目は10個のユニットがあった。各ユニットから1個の数字が得られている。
訓練(学習)などで乱数が使われるため、実行ごとに結果が異なる場合がある。
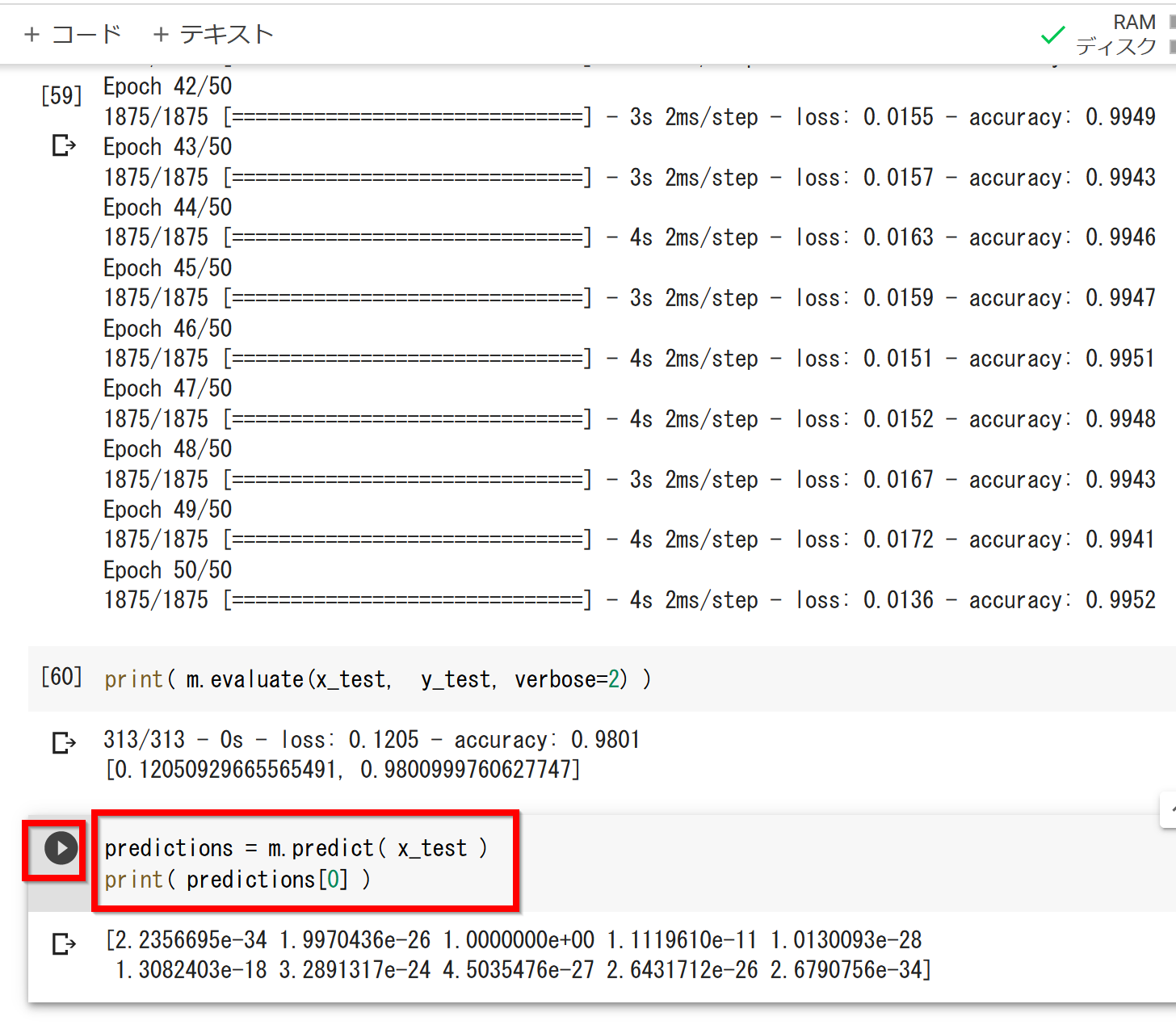
- 正解表示
テスト画像0番の正解を表示する。
print(y_test[0])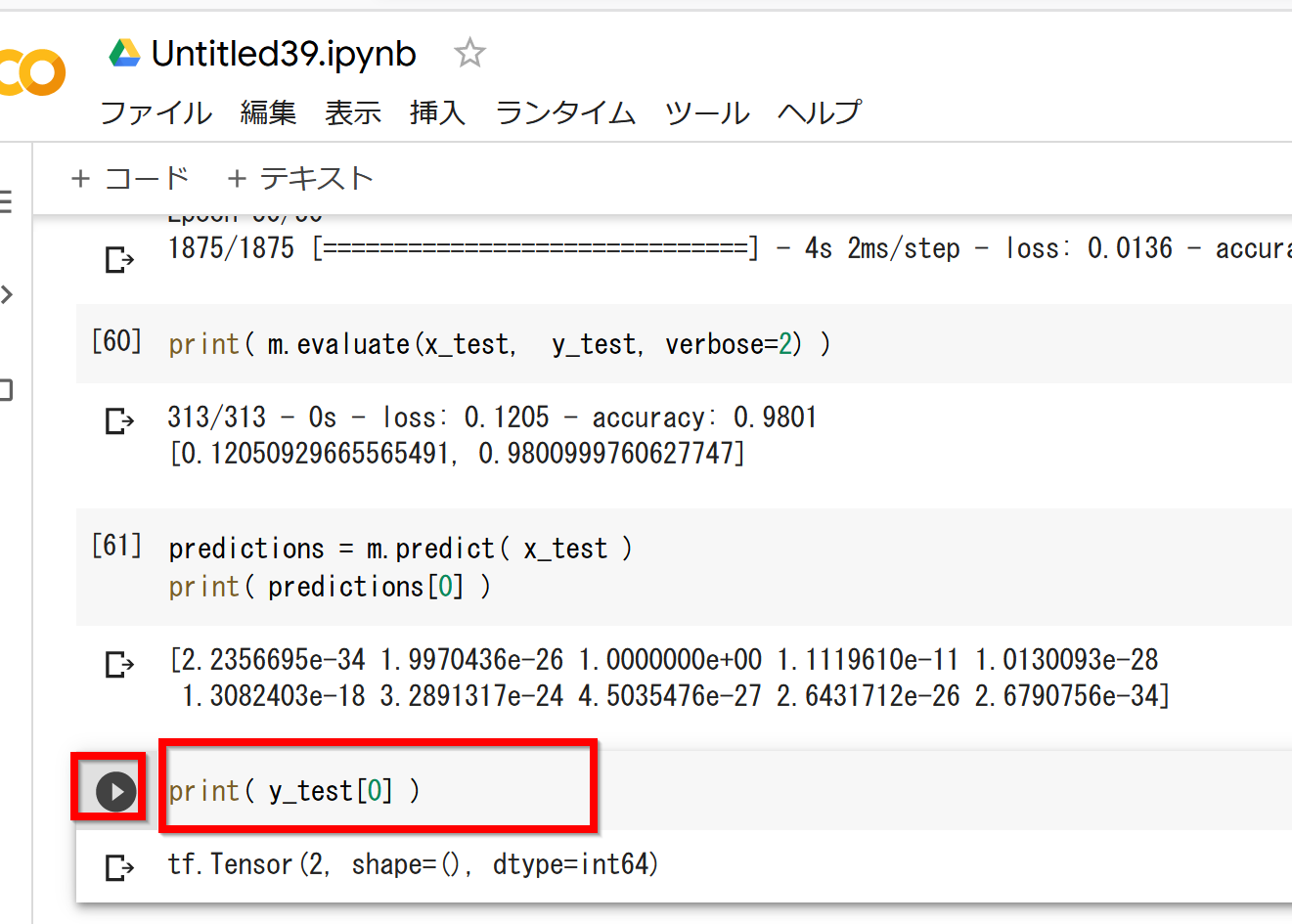
式と変数
変数は、変化するデータのことである。「x = 100」のように書くとxの値が100に変化する。
式の実行結果として値が得られる。式の中に変数名を書くことができる。
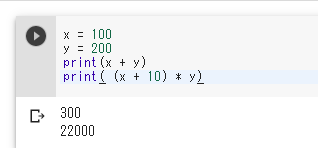
x = 100
y = 200
print(x + y)
print( (x + 10) * y)
teihen = 2.5
takasa = 5
print(teihen * takasa / 2)

関数定義と関数オブジェクト
関数定義はdefを用い、戻り値はreturnで指定する。
- アッカーマン関数の定義
def a(m, n): if m == 0: return n + 1 elif n == 0: return a(m-1, 1) else: return a(m-1, a(m, n-1)) print(a(3, 2)) print(a(m = 3, n = 2)) print(a(n = 2, m = 3))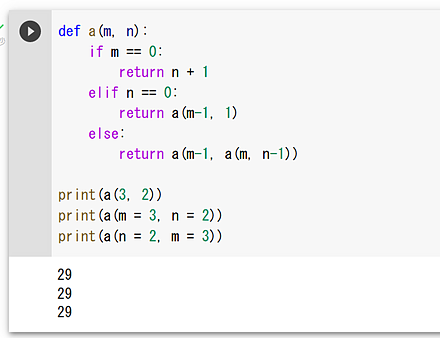
- 既定値(デフォルト値)
def a(m, n = 1): if m == 0: return n + 1 elif n == 0: return a(m-1, 1) else: return a(m-1, a(m, n-1)) print(a(3, 1)) print(a(3)) print(a(m = 3))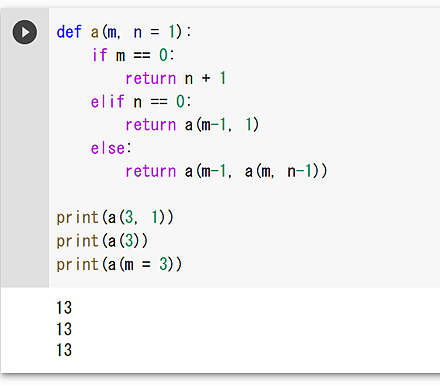
- 関数オブジェクト
f = lambda x: x + 1 print(f(100))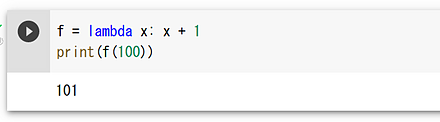
式の抽象化と関数
式の抽象化は、類似した複数の式を変数を使って1つにまとめることである。次の3つの式を考える。
print(100 * 1.08)
print(150 * 1.08)
print(400 * 1.08)
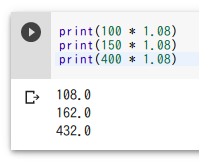
上の3つの式を抽象化すると「a * 1.08」のような式になる。
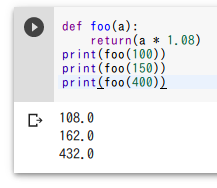
式「a * 1.08」を本体式とするような関数(関数名はfoo)の定義とその使用例を示す。関数の利用により、繰り返し同じことを書くことを防ぐことができ、ミスを減らすこともできる。プログラムの変更も簡単になる。
def foo(a):
return a * 1.08
print(foo(100))
print(foo(150))
print(foo(400))
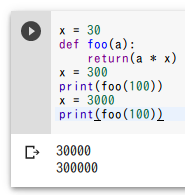
式の評価のタイミング
関数の中の式の評価では、最新の変数値が用いられる。
x = 30
def foo(a):
return(a * x)
x = 300
print(foo(100))
x = 3000
print(foo(100))
クラス定義、オブジェクト生成、属性アクセス
- メソッド: オブジェクトに属する操作や処理
- クラス: 同一種類のオブジェクトの集まり
- クラス定義: あるクラスが持つ属性とメソッドを定めること
- 属性アクセス: 「.」+属性名で属性にアクセスする。メソッド内では、self +「.」で属性にアクセスする
クラス定義、オブジェクト生成、属性アクセスの例
クラス名: C
属性名: qty、weight、name
class C(object):
def __init__(self, qty, weight, name):
self.qty = qty
self.weight = weight
self.name = name
x = C(5, 170.51, 'apple')
y = C(3, 40.97, 'orange')
print(vars(x))
print(vars(y))
print(x.name)
print(y.name)
varsはオブジェクトの属性名と値を取得する。「x.name」、「y.name」は属性アクセスである。
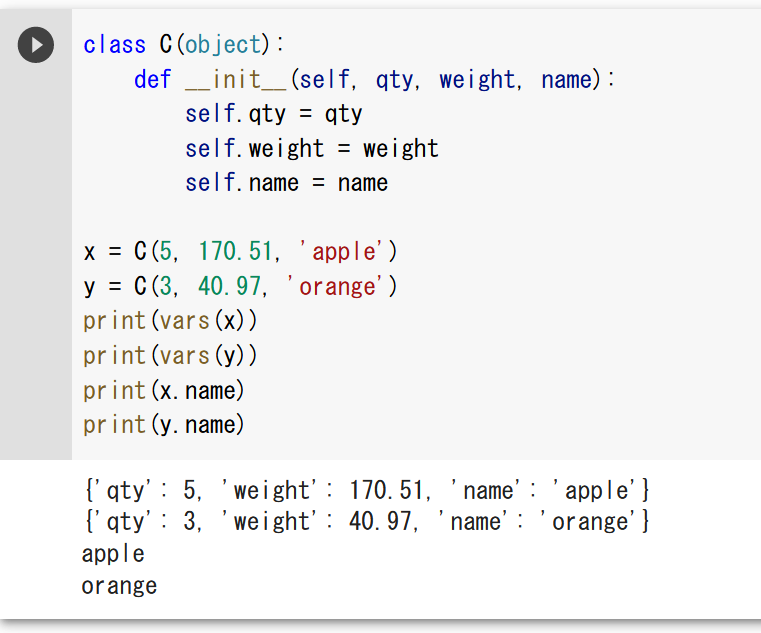
getattrによる属性値の取得
クラス名: C
属性名: qty、weight、name
class C(object):
def __init__(self, qty, weight, name):
self.qty = qty
self.weight = weight
self.name = name
x = C(5, 170.51, 'apple')
y = C(3, 40.97, 'orange')
print(getattr(x, 'qty'))
print(getattr(y, 'weight'))
getattrはオブジェクトと属性名(文字列)を指定して値を取得する。
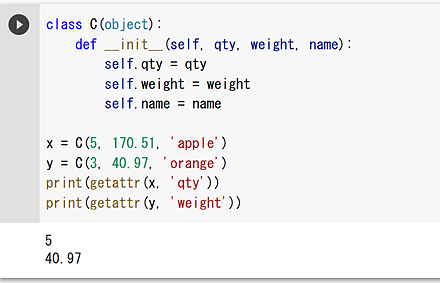
setattrによる属性の動的な追加
クラス名: C
属性名: qty、weight、name
class C(object):
def __init__(self, qty, weight, name):
self.qty = qty
self.weight = weight
self.name = name
x = C(5, 170.51, 'apple')
y = C(3, 40.97, 'orange')
setattr(x, 'color', 'red')
print(vars(x))
print(vars(y))
setattrでは、オブジェクトと属性名(文字列)と値を指定する。
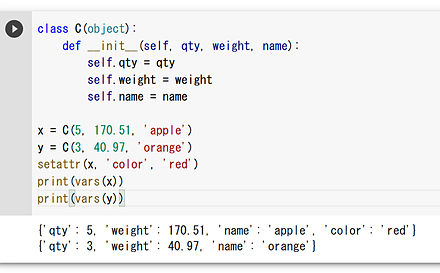
コンストラクタでの既定値(デフォルト値)
既定値(デフォルト値)を設定している場合には、引数を省略できる。コンストラクタ以外のメソッドでも同様である。
クラス名: D
属性名: s_hour、s_minute、e_hour、e_minute
class D(object):
def __init__(self, s_hour, s_minute):
self.s_hour = s_hour
self.s_minute = s_minute
self.e_hour = None
self.e_minute = None
z = D(15, 30)
z2 = D(16, 15)
print(vars(z))
print(vars(z2))

メソッド
メソッドの例
- メソッドアクセス: 「.」+メソッド名でメソッドにアクセスする。メソッド内では、self +「.」で属性やメソッドにアクセスする
class C(object):
def __init__(self, qty, weight, name):
self.qty = qty
self.weight = weight
self.name = name
def total(self):
return self.qty * self.weight
x = C(5, 170.51, 'apple')
print(vars(x))
print(x.total())
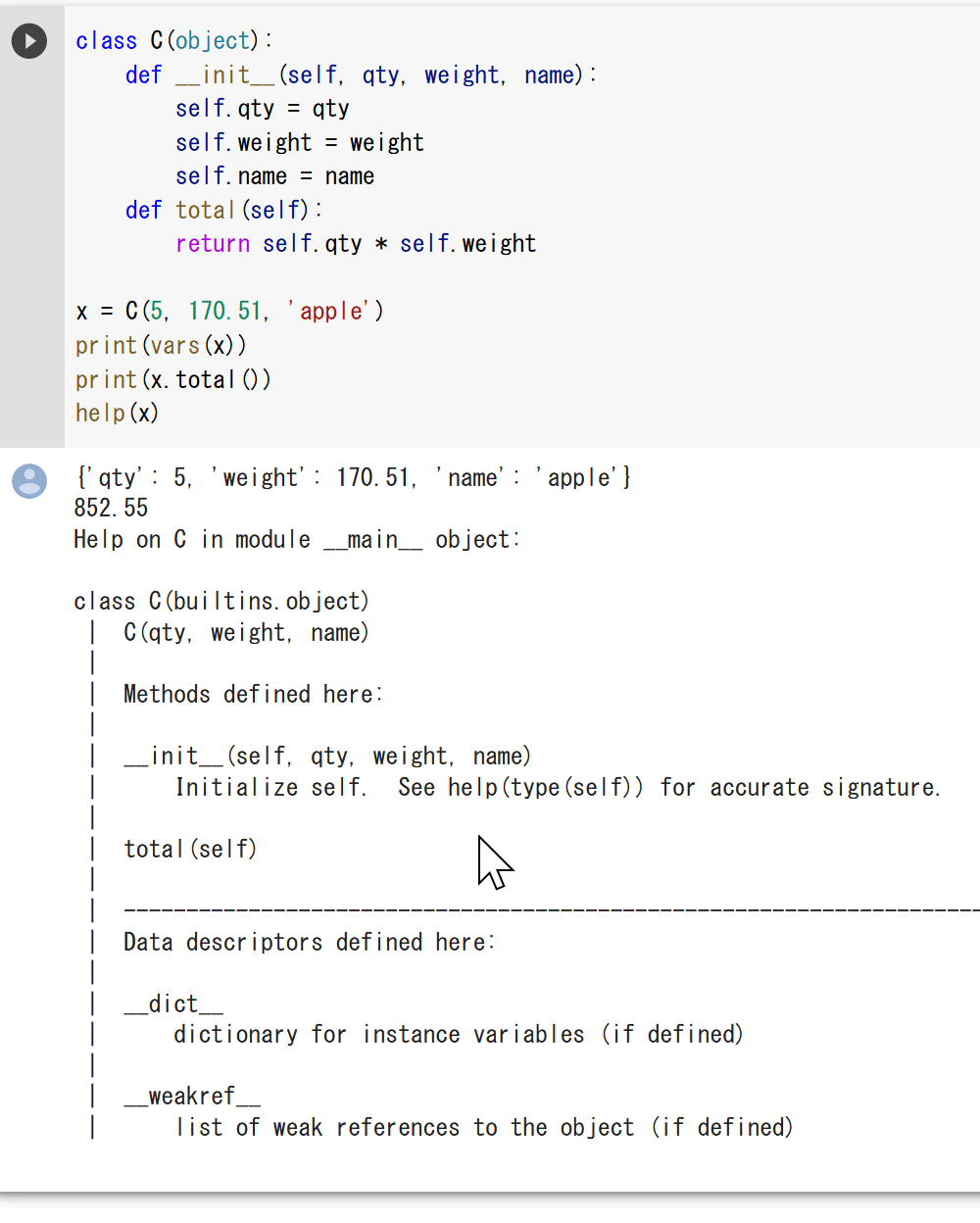
help(x)
helpは、メソッドの説明を表示する。
setattrによるメソッドの追加
class C(object):
def __init__(self, qty, weight, name):
self.qty = qty
self.weight = weight
self.name = name
def total(self):
return self.qty * self.weight
x = C(5, 170.51, 'apple')
setattr(C, 'hoge', lambda self: int(self.weight))
print(x.hoge())
help(x)
スーパークラスからの継承
クラス名: C
属性名: qty、weight、name
クラス名: E
属性名: qty、weight、name、price
クラスEは、スーパークラスであるクラスCの属性とメソッドを継承する。
class C(object):
def __init__(self, qty, weight, name):
self.qty = qty
self.weight = weight
self.name = name
def total(self):
return self.qty * self.weight
class E(C):
def __init__(self, qty, weight, name, price):
super(E, self).__init__(qty, weight, name)
self.price = price
def payment(self):
return self.qty * self.price
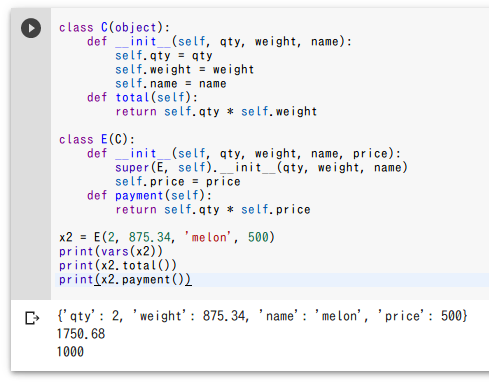
x2 = E(2, 875.34, 'melon', 500)
print(vars(x2))
print(x2.total())
print(x2.payment())
ファイルの選択
ファイルダイアログ(tkinterを使用)
次のPythonプログラムは、tkinterのfiledialogを使用し、ファイルを選択するためのダイアログを表示する。
import tkinter as tk
from tkinter import filedialog
root = tk.Tk()
root.withdraw()
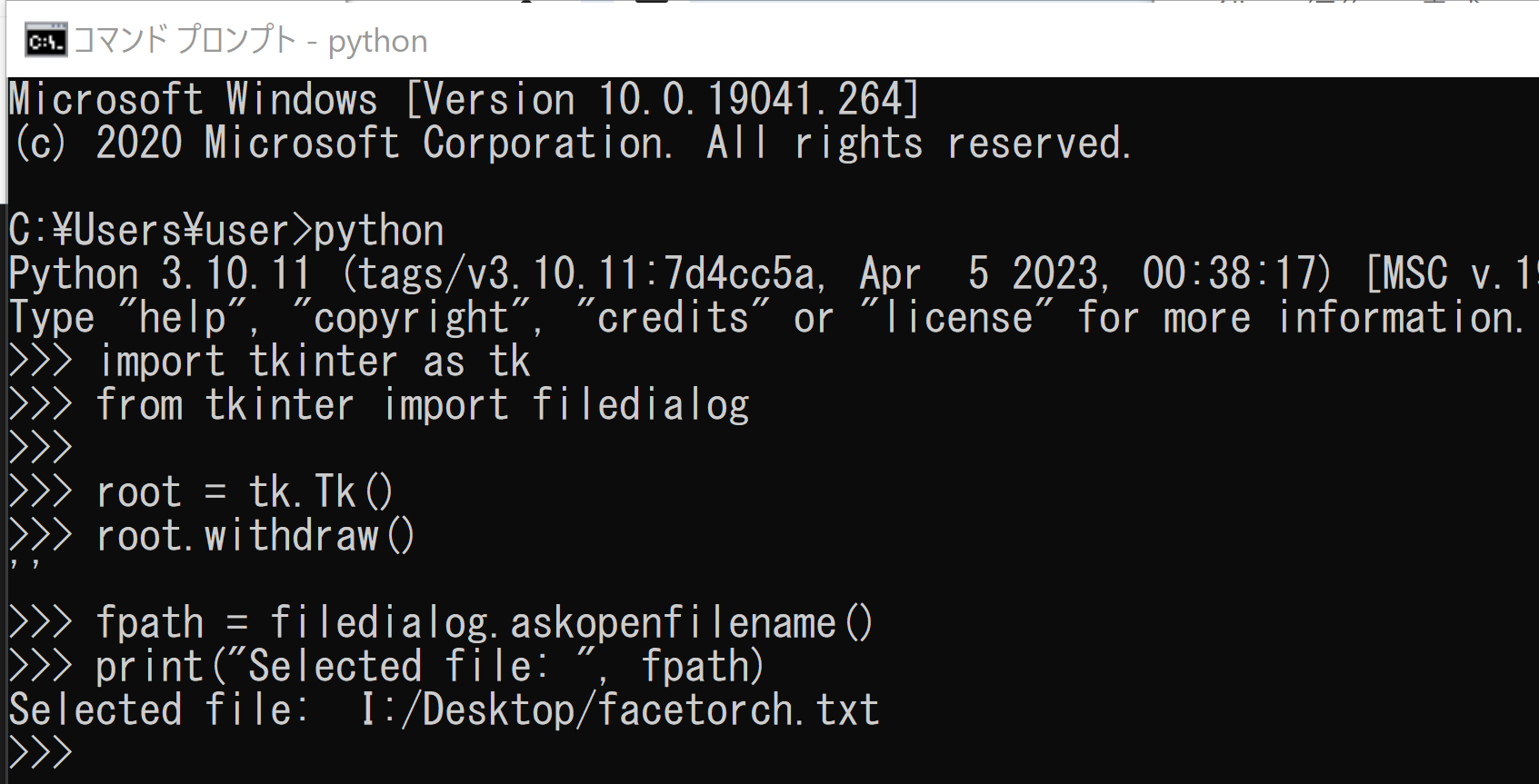
fpath = filedialog.askopenfilename()
print("Selected file: ", fpath)
このプログラムを実行すると、ファイルダイアログが表示され、選択したファイルのパスが表示される。
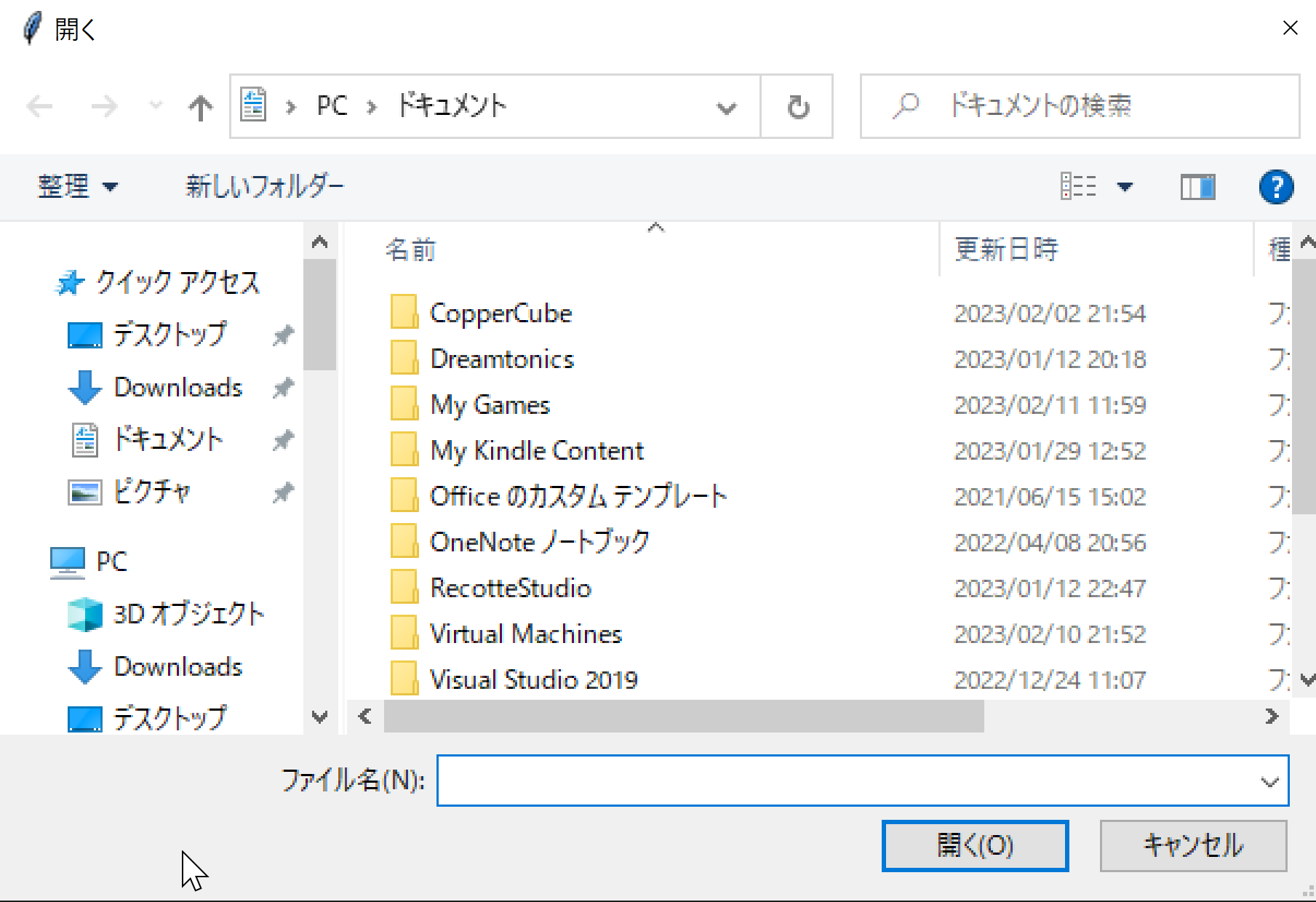
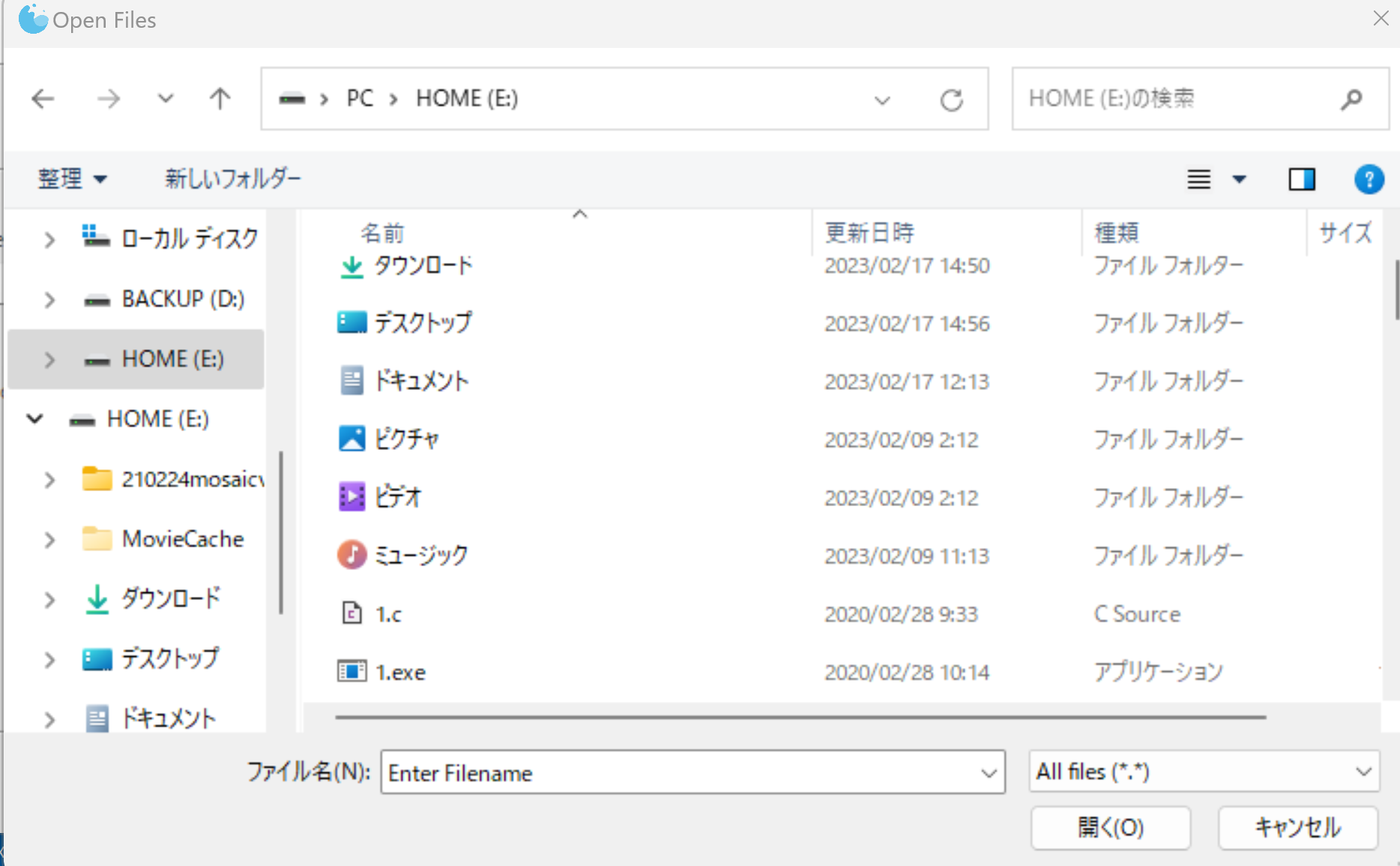
次のPythonプログラムは、tkinterのfiledialogを使用し、複数のファイルを選択するためのダイアログを表示する。
import tkinter as tk
from tkinter import filedialog
root = tk.Tk()
root.withdraw()
fpaths = filedialog.askopenfilenames()
for fpath in root.tk.splitlist(fpaths):
print("Selected file: ", fpath)
ファイルを1つ選択(pysimpleguiを使用)
次のプログラムは、PNGファイルを1つ選び、myinput.pngというファイル名にコピーする。
「python -m pip install -U pysimplegui」でインストールを行っておく。
import PySimpleGUI as sg
import shutil
layout = [
[sg.Text('png file', size=(8, 1)), sg.Input(), sg.FileBrowse()],
[sg.Submit(), sg.Cancel()]]
window = sg.Window('PNG File Upload', layout)
event, values = window.read()
window.close()
shutil.copyfile(values[0], "myinput.png")
ファイルを複数選択(gooeyを使用)
次のプログラムは、ファイルを複数選択し、選択されたファイル名を表示する。
「python -m pip install -U gooey」でインストールを行っておく。
from gooey import Gooey, GooeyParser
@Gooey(required_cols=0)
def main():
parser = GooeyParser(description='Process something.')
parser.add_argument('-i', '--infiles', nargs='*', metavar='InFiles', help='Choose one file or more-than-on files!', widget="MultiFileChooser")
parser.add_argument('-n', '--name', metavar='Name', help='Enter some text!')
parser.add_argument('-f', '--foo', metavar='Flag 1', action='store_true', help='I turn things on and off')
parser.add_argument('-b', '--bar', metavar='Flag 2', action='store_true', help='I turn things on and off')
a = parser.parse_args()
print(a.infiles)
print(a.name)
print(a.foo)
print(a.bar)
if __name__ == '__main__':
main()
画像ファイルの表示、画像ファイルのサイズの取得
PILのshowを使用して画像ファイルを表示する。
from PIL import Image
Image.open('1.png').show()
MatplotLibを使用して画像ファイルを表示する。
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
img = mpimg.imread('1.png')
plt.imshow(img)
plt.show()
PILを使用して画像のサイズを取得する。
from PIL import Image
width, height = Image.open(image_path).size
print(width, height)
ply ファイルの表示
次のプログラムは,ファイルダイヤログにより ply ファイルを1つ選択ののち,表示を行うプログラムである.マウスの左クリックとマウス移動により回転できる.マウスホイールにより,前後移動する.
import pygame
from pygame.locals import *
from OpenGL.GL import *
from OpenGL.GLUT import *
from OpenGL.GLU import *
from plyfile import PlyData, PlyElement
# PLYファイルを読み込む
import tkinter as tk
from tkinter import filedialog
root = tk.Tk()
root.withdraw()
fpath = filedialog.askopenfilename()
plydata = PlyData.read(fpath)
vertex_data = plydata['vertex'].data
face_data = plydata['face'].data
# 頂点と面をリストとして取得
vertices = [list(elem) for elem in vertex_data]
faces = [face[0] for face in face_data]
# PygameとOpenGLを初期化
pygame.init()
display = (800, 600)
pygame.display.set_mode(display, DOUBLEBUF | OPENGL)
gluPerspective(45, (display[0] / display[1]), 0.1, 50.0)
glTranslatef(0.0, 0.0, -5)
# マウス操作のための変数
rotation_enabled = False
rotation_start = (0, 0)
zoom = 0.0
# メインループ
while True:
for event in pygame.event.get():
if event.type == pygame.QUIT:
pygame.quit()
quit()
elif event.type == pygame.MOUSEBUTTONDOWN:
if event.button == 1: # 左クリック
rotation_enabled = True
rotation_start = pygame.mouse.get_pos()
elif event.button == 4: # ホイール回転(上方向)
zoom = 1
elif event.button == 5: # ホイール回転(下方向)
zoom = -1
elif event.type == pygame.MOUSEBUTTONUP:
if event.button == 1: # 左クリック解除
rotation_enabled = False
elif event.type == pygame.MOUSEMOTION:
if rotation_enabled:
dx = event.pos[0] - rotation_start[0]
dy = event.pos[1] - rotation_start[1]
glRotatef(dx, 0, 1, 0) # y軸周りに回転
glRotatef(dy, 1, 0, 0) # x軸周りに回転
rotation_start = event.pos
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
# 視点の移動範囲を制限
max_zoom = 5.0
min_zoom = -5.0
zoom = max(min_zoom, min(max_zoom, zoom))
glTranslatef(0.0, 0.0, -zoom)
zoom = 0
glBegin(GL_TRIANGLES)
for face in faces:
for vertex_i in face:
glVertex3fv(vertices[vertex_i][:3])
glEnd()
pygame.display.flip()
pygame.time.wait(10)
行列計算の基礎と実装
別ページに引っ越しました:引越し先は https://www.kkaneko.jp/ai/st/matrixcalc.html
音声信号処理の基礎と実装
別ページに引っ越しました:引越し先は https://www.kkaneko.jp/ai/st/sound.html
![[kaneko lab.]](https://www.kkaneko.jp/info/logo_png.png)