Octaveによる統計計算と分析の基本機能

Octave のインストール手順（Windows上）

1. インストーラーの入手：公式サイト GNU Octave の"Windows Installers"セクションから，最新の安定版64bit版インストーラーをダウンロードする．
2. 管理者権限での実行：ダウンロードしたインストーラーを右クリックし，「管理者として実行」を選択する．セキュリティ警告が表示された場合は「実行」を選択する．
3. インストール言語：English（デフォルト）を選択し，「Next」をクリックする．現時点で日本語インターフェースには対応していない．
4. ライセンス同意：条項を確認し，「I accept the agreement」を選択して「Next」をクリックする．
5. インストール先の指定：デフォルトのパス（C:\Program Files\GNU Octave）を推奨する．重要：パスにスペースや日本語文字を含めないようにすること．
6. コンポーネントの選択：以下の項目すべてを選択する．
   • Full installation（完全インストール）
   • Create Desktop Icon（デスクトップアイコンの作成）
   • Associate .m files with GNU Octave（.mファイルの関連付け）
7. インストール実行：「Install」をクリックしてインストールを開始する．
8. 初期動作確認：インストール完了後，以下の手順で動作を確認する：
   1. デスクトップ上のOctaveアイコンをダブルクリック
   2. コマンドウィンドウが開き，プロンプト（octave:）が表示されることを確認
   3. version コマンドを実行してバージョンを確認
   4. 2 + 2 を実行し動作を確認
   5. plot([1,2,3]) を実行し，グラフ描画を確認する．

Octaveによる統計計算と分析

平均

• 行ベクトルの平均

  「mean([1 2 3 4])」は，行ベクトル [1 2 3 4] の平均値を求める．

  X が行ベクトルの場合，mean(X, OPT) として OPT を指定できる．OPT は計算方法の指定である（省略可能）．

  • "a" ・・・　算術平均（デフォルト）
  • "g" ・・・　幾何平均
  • "h" ・・・　調和平均
  
  mean を用いた行ベクトルの平均
• 行列の平均

  X が行列の場合，mean(X, DIM, OPT) として DIM, OPT を指定できる（省略可能）．

  • DIM=1 ・・・ 列方向の計算（デフォルト）
  • DIM=2 ・・・ 行方向の計算
  
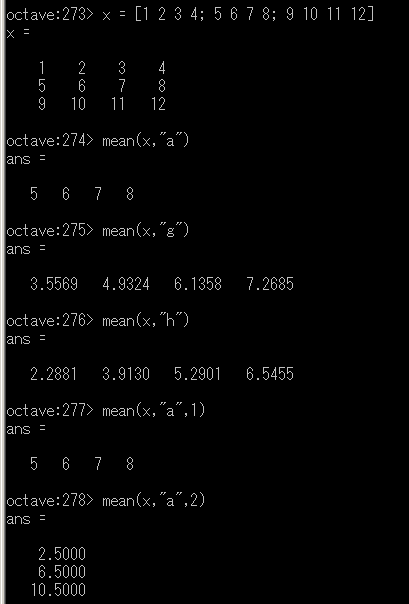
  mean を用いた行列の平均．DIM=1 は列方向，DIM=2 は行方向の計算

二乗和

• 行ベクトルの二乗和

  各要素を二乗して合計した値を求める．

  
  sumsq を用いた行ベクトルの二乗和
• 行列の二乗和

  X が行列の場合，sumsq(X, DIM) として DIM を指定できる（省略可能）．

  • DIM=1 ・・・ 列方向の計算（デフォルト）
  • DIM=2 ・・・ 行方向の計算
  
  sumsq を用いた行列の二乗和．DIM=1 は列方向，DIM=2 は行方向の計算

分散

「var(X)」はデータのばらつきを表す値である．

var (x) = sum(power(x-mean(x), 2))/(length(x)-1)

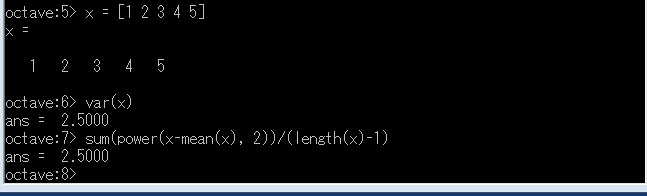
• 行ベクトルの分散

  X が行ベクトルの場合，var(X, OPT) として OPT を指定できる（省略可能）．

  • OPT=0 ・・・　N-1 で正規化（デフォルト）
  • OPT=1 ・・・　N で正規化
  
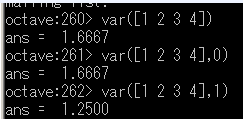
  var を用いた行ベクトルの分散
• 行列の分散

  X が行列の場合，var(X, OPT, DIM) として DIM, OPT を指定できる（省略可能）．

  • DIM=1 ・・・ 列方向の計算（デフォルト）
  • DIM=2 ・・・ 行方向の計算
  
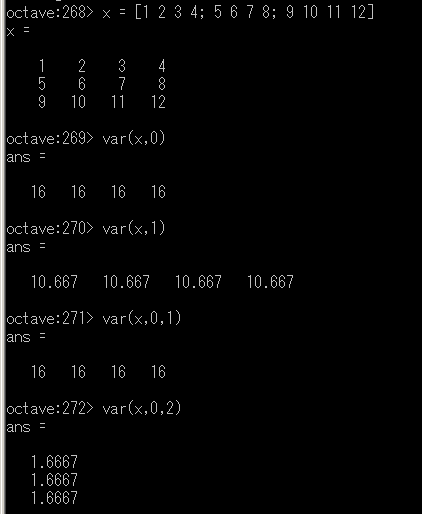
  var を用いた行列の分散

標準偏差

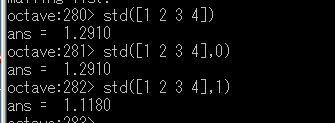
「std(X)」は分散の正の平方根である．

std (x) = sqrt (sumsq (x - mean (x)) / (n - 1))

• 行ベクトルの標準偏差

  X が行ベクトルの場合，std(X, OPT) として OPT を指定できる（省略可能）．

  • OPT=0 ・・・　不偏分散の平方根（デフォルト）
  • OPT=1 ・・・　標本分散の平方根
  
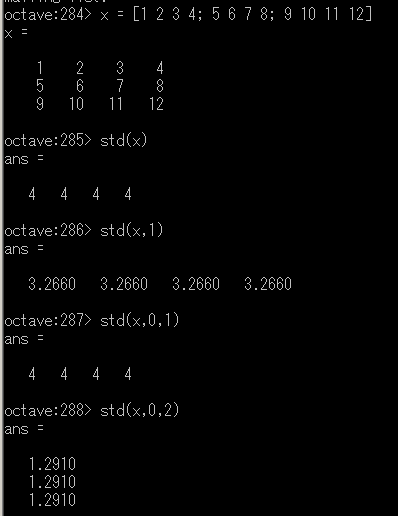
  std を用いた行ベクトルの標準偏差
• 行列の標準偏差

  X が行列の場合，std(X, OPT, DIM) として DIM, OPT を指定できる（省略可能）．

  • DIM=1 ・・・ 列方向の計算（デフォルト）
  • DIM=2 ・・・ 行方向の計算
  
  std を用いた行列の標準偏差

平均を引く

• 行ベクトルの場合

  X が行ベクトルの場合，center(X) は各要素から平均を引いた値を求める．

• 行列の場合

  X が行列の場合，center(X, DIM) として DIM を指定できる（省略可能）．

  • DIM=1 ・・・ 列方向の計算（デフォルト）
  • DIM=2 ・・・ 行方向の計算

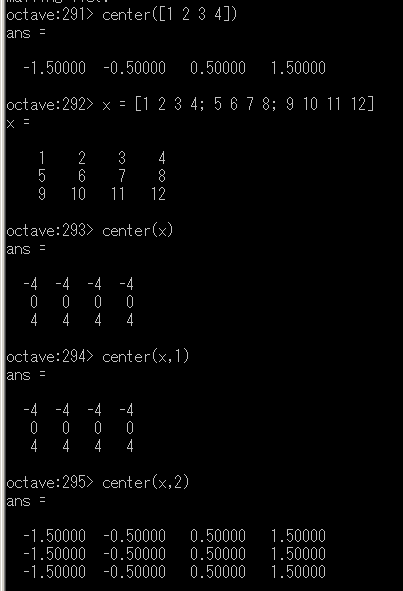
center の例

平均を引き，標準偏差で割る

• 行ベクトルの場合

  X が行ベクトルの場合，studentize(X) は各要素から平均を引き，標準偏差で割った値を求める．

• 行列の場合

  X が行列の場合，studentize(X, DIM) として DIM を指定できる（省略可能）．

  • DIM=1 ・・・ 列方向の計算（デフォルト）
  • DIM=2 ・・・ 行方向の計算
  
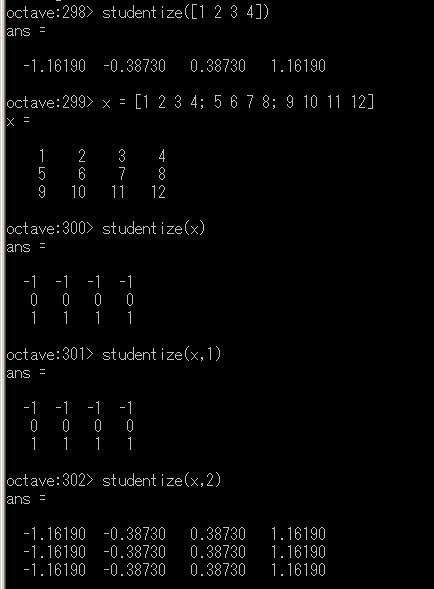
  studentize の例

尖度

長さ N のベクトルに対して次の式で計算する．

kurtosis(x) = N^(-1) std(x)^(-4) sum((x - mean(x)).^4) - 3

歪度

長さ N のベクトルに対して次の式で計算する．

skewness(x) = N^(-1) std(x)^(-3) sum((x - mean(x)).^3)

統計

次の統計量を求める：最小値，第1四分位数，中央値，第3四分位数，最大値，平均，標準偏差，歪度，尖度

• 行ベクトルの場合

  X が行ベクトルの場合，statistics(X) は列ベクトルとみなして計算する．

• 行列の場合

  X が行列の場合，statistics(X) は列方向で計算する．

  
  statistics の例

QQプロット

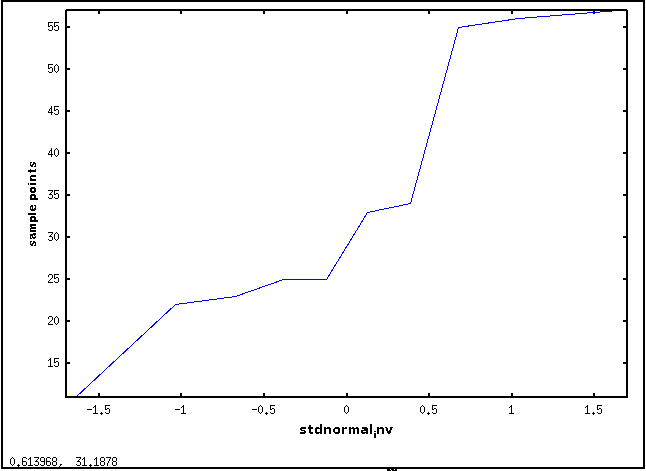
QQ プロットの例

マハラノビス距離

mahalanobis(X,Y) は X と Y のマハラノビスの D-平方距離を求める．

スピアマンの順位相関係数

spearman(X,Y) は X と Y の順位相関係数を求める．

• 分散共分散行列

  cov(X,Y) は列数 N の 2 つの行列から N 行 M 列の分散共分散行列を求める．行数は一致している必要がある．

  
  分散共分散行列の例
• 相関係数行列

  corrcoef(X,Y) は列数 N の 2 つの行列から N 行 M 列の相関係数行列を求める．行数は一致している必要がある．

  corrcoef(x,y) = cov(x,y)/(std(x)*std(y))
  

  
  相関係数行列の例
• 相関係数

  cor は相関係数を求める関数である．

  
  cor の例

確率分布

• 正規分布関数

  正規分布の確率密度関数（PDF）と累積分布関数（CDF）を計算する．

  • normpdf(X, MU, SIGMA) は，平均 MU，標準偏差 SIGMA の正規分布の確率密度を求める．MU，SIGMA は省略可能であり，その場合は標準正規分布（MU=0，SIGMA=1）となる．
  • normcdf(X, MU, SIGMA) は，平均 MU，標準偏差 SIGMA の正規分布の累積分布を求める．MU，SIGMA は省略可能であり，その場合は標準正規分布（MU=0，SIGMA=1）となる．
• t分布関数

  t分布の確率密度関数（PDF）と累積分布関数（CDF）を計算する．

  • tpdf(X, NU) は，自由度 NU の t分布の確率密度を求める．
  • tcdf(X, NU) は，自由度 NU の t分布の累積分布を求める．
• カイ二乗分布関数

  カイ二乗分布の確率密度関数（PDF）と累積分布関数（CDF）を計算する．

  • chi2pdf(X, NU) は，自由度 NU のカイ二乗分布の確率密度を求める．
  • chi2cdf(X, NU) は，自由度 NU のカイ二乗分布の累積分布を求める．
• F分布関数

  F分布の確率密度関数（PDF）と累積分布関数（CDF）を計算する．

  • fpdf(X, NU1, NU2) は，分子の自由度 NU1，分母の自由度 NU2 の F分布の確率密度を求める．
  • fcdf(X, NU1, NU2) は，分子の自由度 NU1，分母の自由度 NU2 の F分布の累積分布を求める．

分位点の計算

• norminv(P, MU, SIGMA)

  正規分布の逆累積分布関数であり，確率 P に対応する分位点を求める．

• tinv(P, NU)

  t分布の逆累積分布関数であり，確率 P に対応する分位点を求める．

• chi2inv(P, NU)

  カイ二乗分布の逆累積分布関数であり，確率 P に対応する分位点を求める．

• finv(P, NU1, NU2)

  F分布の逆累積分布関数であり，確率 P に対応する分位点を求める．

仮説検定

• 1標本のt検定

  ttest(X, M) は，ベクトル X の平均が M に等しいという帰無仮説を検定する．

  • H0: 母平均 = M（帰無仮説）
  • H1: 母平均 ≠ M（対立仮説）

  戻り値は [H, P, CI] の形式であり，H は検定結果（H=1 で帰無仮説を棄却），P は p 値，CI は信頼区間である．

• 2標本のt検定

  ttest2(X, Y) は，2つのベクトル X と Y の母平均が等しいという帰無仮説を検定する．

  • H0: 2つの母平均は等しい（帰無仮説）
  • H1: 2つの母平均は異なる（対立仮説）

  戻り値は [H, P, CI] の形式であり，H は検定結果（H=1 で帰無仮説を棄却），P は p 値，CI は信頼区間である．

• カイ二乗検定

  chi2test(O, E) は，観測度数 O と期待度数 E の差の検定を行う．

  • H0: 観測度数と期待度数の差は偶然による（帰無仮説）
  • H1: 観測度数と期待度数の差は有意である（対立仮説）

  戻り値は [P, CHI2STAT] の形式であり，P は p 値，CHI2STAT はカイ二乗統計量である．

• F検定

  vartest2(X, Y) は，2つのベクトル X と Y の母分散が等しいという帰無仮説を検定する．

  • H0: 2つの母分散は等しい（帰無仮説）
  • H1: 2つの母分散は異なる（対立仮説）

  戻り値は [H, P, CI, STATS] の形式であり，H は検定結果（H=1 で帰無仮説を棄却），P は p 値，CI は信頼区間，STATS は検定統計量である．

データの可視化

• ヒストグラム

  hist(X) は，データの度数分布を棒グラフで表示する．

  • hist(X, NBINS) は，ビンの数を NBINS に指定する．
  • hist(X, CENTERS) は，ビンの中心を CENTERS で指定する．
  • [N, X] = hist(...) は，ビンの度数 N とビンの中心位置 X を返す．
• 箱ひげ図

  boxplot(X) は，データの分布を四分位数と外れ値で表示する．

  • boxplot(X, G) は，グループ G ごとの箱ひげ図を表示する．
  • boxplot({X1, X2, ...}) は，複数のデータセットの箱ひげ図を表示する．
  • [S, H] = boxplot(...) は，統計量 S とハンドル H を返す．
• 散布図

  scatter(X, Y) は，2つの変数の関係を点で表示する．

  • scatter(X, Y, S) は，点の大きさを S で指定する．
  • scatter(X, Y, S, C) は，点の色を C で指定する．
  • H = scatter(...) は，グラフのハンドル H を返す．
• 確率プロット

  probplot(X) は，データが正規分布に従うかを確認するためのプロットを表示する．

  • probplot(X, 'distribution') は，指定した分布との適合度を確認する．
  • [H, STATS] = probplot(...) は，ハンドル H と統計量 STATS を返す．

  'distribution' には次の値を指定できる．

  • 'normal' ・・・ 正規分布（デフォルト）
  • 'exponential' ・・・ 指数分布
  • 'extreme value' ・・・ 極値分布
  • 'rayleigh' ・・・ レイリー分布
  • 'weibull' ・・・ ワイブル分布