統計分析のPython 実現ガイド
【目次】
【サイト内のPython関連主要ページ】
- Windows AI支援Python開発環境構築ガイド: 別ページ »で説明
- AIエディタ Windsurf の活用: 別ページ »で説明
- AIエディタCursorガイド: 別ページ »で説明
- Google Colaboratory: 別ページ »で説明
- Python(Google Colaboratoryを含む)のまとめ: 別ページ »で説明
- 機械学習の Python 実現ガイド: 別ページ »で説明
- 行列計算の Python 実現ガイド: 別ページ »で説明
- 統計分析のPython での実現ガイド: 別ページ »で説明
- 音声信号処理の Python 実現ガイド: 別ページ »で説明
- カラー画像処理の Python 実現ガイド: 別ページ »で説明
- Python 言語によるとても簡単なアドベンチャーゲーム(変数,式,if,while,関数,print,time.sleep, def, global を使用): 別ページ »で説明
- Pythonプログラミング講座:基礎から応用まで(授業資料,全15回): 別ページ »で説明
- Pythonプログラミングの例と実践ガイド: 別ページ »で説明
【外部リソース】
- Pythonの公式サイト: https://www.python.org
- 東京大学の「Pythonプログラミング入門」: https://utokyo-ipp.github.io/IPP_textbook.pdf
- ITmedia社の「Pythonチートシート」の記事: https://atmarkit.itmedia.co.jp/ait/articles/2004/20/news015.html
統計手法
- 記述統計量
- ヒストグラム
- クロス集計表
- 検定
記述統計量
記述統計量は、データセットの特徴を数値で要約する統計指標である。データ全体の特性を把握し、適切な分析手法の選択に役立つ。
基本的な統計量として以下が挙げられる。
- 平均値(データの中心傾向を示す指標)
- 標準偏差(データのばらつきを示す統計量)
- 中央値(データの中心的傾向を示す指標)
- 四分位数(分布の形状を示す統計量)
- 最大値(データセットの上限値)
- 最小値(データセットの下限値)
- 分散(データの変動性を示す指標)
- 歪度(分布の非対称性を示す統計量)
- 尖度(分布の尖り具合を示す統計量)
用語リスト
- 記述統計量: データ分析の基本となる数値指標の総称である。平均値、標準偏差、中央値などを含み、データの特徴把握に用いる。
- 平均値: データの総和をデータ数で除した値であり、データ分布の中心傾向を示す。外れ値の影響を受けやすい。
- 標準偏差: データのばらつきを示す指標であり、平均値からの平均的な距離を表す。値が大きいほどばらつきが大きい。
- 中央値: 順序付けられたデータの中央に位置する値である。外れ値の影響を受けにくく、非対称な分布で有用である。
- 四分位数: データを4等分する境界値であり、第1四分位数、中央値、第3四分位数から構成される。分布形状の把握と外れ値の検出に用いる。
- 最大値: データセット内の最高値である。最小値とともにデータの範囲を示す。
- 最小値: データセット内の最低値である。最大値とともにデータの範囲を示す。
- 分散: データの散らばりを表す統計量であり、各データ点と平均値の差の二乗平均である。標準偏差の二乗に等しい。
- 歪度: 分布の非対称性を示す指標である。正規分布では0となり、正の値は右に、負の値は左に裾が長い分布を示す。
- 尖度: 分布の尖り具合を示す指標である。scipy.stats.kurtosis()は超過尖度を返し、正規分布で0となる。正の値は正規分布より尖った分布、負の値は平坦な分布を示す。
- pandas: データ分析用のPythonライブラリである。記述統計量の計算やデータ処理機能を提供し、describeメソッドで主要な統計量を一括算出できる。
- 属性: データベースやデータフレームにおける各列を表す要素である。
- データフレーム: 行と列で構成される2次元のデータ構造であり、pandasの中核機能である。複数の属性と観測値を管理する。
- 外れ値: データセット内で他のデータから大きく離れた値である。統計分析結果に影響するため、適切な処理が必要である。
- 分布: データの散らばり方や偏りを示す概念である。記述統計量でその特徴を数値的に把握する。
- ヒストグラム: データの分布を視覚的に表現するグラフである。データの範囲を区間に分割し、各区間の頻度を棒グラフで表示する。
- 箱ひげ図: データの分布を視覚化するグラフであり、中央値、四分位数、最大値、最小値を一度に表示できる。外れ値の検出やグループ間の比較に用いる。
- クロス集計表: 2つの変数間の関係性を表形式で示す分析手法である。行と列の変数の組み合わせごとの度数を表示する。
- 帰無仮説: 統計的検定において「差がない」「効果がない」と仮定する仮説である。検定ではこの仮説を棄却できるかを判断する。
- 有意水準: 帰無仮説を棄却する基準となる確率である。一般的に5%(0.05)または1%(0.01)を用い、p値がこの値を下回ると統計的に有意と判断する。
- t検定: 2群の平均値の差の統計的有意性を評価する検定手法である。帰無仮説「2群の母平均が等しい」に対してp値を算出する。
- Welchのt検定: 2群の分散が等しくない場合に用いるt検定の拡張形である。等分散を仮定しないため、通常のt検定より適用範囲が広い。
- ノンパラメトリック検定: 母集団分布の形状を仮定しない検定手法である。順位や符号を用いて検定を行い、正規分布を仮定できないデータに適用する。
- Mann-Whitney U検定: 独立した2群の分布の差を検定するノンパラメトリック手法である。Wilcoxon順位和検定とも呼ばれる。正規性を仮定できない場合にt検定の代替として用いる。
- 一元配置分散分析: 3群以上の平均値の差を同時に検定する統計手法である。t検定は2群間の比較に限られるため、3群以上の比較にはこの手法を用いる。
- Shapiro-Wilk検定: データの正規性を評価する検定手法である。帰無仮説「母集団が正規分布に従う」に対してp値を算出する。パラメトリック検定の適用可否を判断する際に用いる。
- p値: 帰無仮説が真である場合に、観測データ以上に極端な結果が得られる確率である。有意水準(一般的に5%)未満であれば統計的に有意と判断する。
- データ分析: 収集されたデータから有用な情報や知見を抽出するプロセスである。記述統計量の算出は初期段階として、分析の方向性を決定する。
- 統計指標: データの特徴を数値化して表現する指標である。記述統計量はその代表例であり、データの性質や傾向を客観的に評価する基準となる。
統計処理の比較
以下の表は、同じ統計処理を異なるツールで実行する際のコマンドを比較したものである。
| 処理内容 | SPSS | R | Python (pandas/scipy) |
|---|---|---|---|
| 記述統計量 | DESCRIPTIVES、FREQUENCIES |
summary、sd、skewness、kurtosis |
df.describe()、stats.skew()、stats.kurtosis() |
| 頻度表 | FREQUENCIES |
table |
value_counts() |
| クロス集計表 | CROSSTABS |
table |
pd.crosstab() |
| 集約 | AGGREGATE |
aggregate |
groupby().agg() |
| Welchのt検定 | T-TEST |
t.test |
stats.ttest_ind() |
| 一元配置分散分析 | ONEWAY |
oneway.test |
stats.f_oneway() |
| Mann-Whitney U検定 | NPAR TESTS |
wilcox.test |
stats.mannwhitneyu() |
Pythonプログラム例
本節で使用するデータセットの構造を以下に示す。
| 科目 | 受講者 | 得点 |
|---|---|---|
| 国語 | A | 90 |
| 国語 | B | 80 |
| 算数 | A | 95 |
| 算数 | B | 90 |
| 理科 | A | 80 |
前準備
Python 3.12 のインストール
以下のいずれかの方法で Python 3.12 をインストールする。
方法1:winget によるインストール
Python がインストール済みの場合、この手順は不要である。管理者権限のコマンドプロンプトで以下を実行する。管理者権限のコマンドプロンプトを起動するには、Windows キーまたはスタートメニューから「cmd」と入力し、表示された「コマンドプロンプト」を右クリックして「管理者として実行」を選択する。
winget install -e --id Python.Python.3.12 --scope machine --silent --accept-source-agreements --accept-package-agreements --override "/quiet InstallAllUsers=1 PrependPath=1 AssociateFiles=1 InstallLauncherAllUsers=1"--scope machine を指定することで、システム全体(全ユーザー向け)にインストールされる。このオプションの実行には管理者権限が必要である。インストール完了後、コマンドプロンプトを再起動すると PATH が自動的に設定される。
方法2:インストーラーによるインストール
- Python 公式サイト(https://www.python.org/downloads/)にアクセスし、「Download Python 3.x.x」ボタンから Windows 用インストーラーをダウンロードする。
- ダウンロードしたインストーラーを実行する。
- 初期画面の下部に表示される「Add python.exe to PATH」に必ずチェックを入れてから「Customize installation」を選択する。このチェックを入れ忘れると、コマンドプロンプトから
pythonコマンドを実行できない。 - 「Install Python 3.xx for all users」にチェックを入れ、「Install」をクリックする。
インストールの確認
コマンドプロンプトで以下を実行する。
python --versionバージョン番号(例:Python 3.12.x)が表示されればインストール成功である。「'python' は、内部コマンドまたは外部コマンドとして認識されていません。」と表示される場合は、インストールが正常に完了していない。
AIエディタ Windsurf のインストール
Pythonプログラムの編集・実行には、AIエディタの利用を推奨する。ここでは、Windsurfのインストールを説明する。
Windsurf がインストール済みの場合、この手順は不要である。管理者権限のコマンドプロンプトで以下を実行する。管理者権限のコマンドプロンプトを起動するには、Windows キーまたはスタートメニューから「cmd」と入力し、表示された「コマンドプロンプト」を右クリックして「管理者として実行」を選択する。
winget install -e --id Codeium.Windsurf --scope machine --accept-source-agreements --accept-package-agreements --override "/VERYSILENT /NORESTART /MERGETASKS=!runcode,addtopath,associatewithfiles,!desktopicon"
powershell -Command "$env:Path=[System.Environment]::GetEnvironmentVariable('Path','Machine')+';'+[System.Environment]::GetEnvironmentVariable('Path','User'); windsurf --install-extension MS-CEINTL.vscode-language-pack-ja --force; windsurf --install-extension ms-python.python --force"--scope machine を指定することで、システム全体(全ユーザー向け)にインストールされる。このオプションの実行には管理者権限が必要である。インストール完了後、コマンドプロンプトを再起動すると PATH が自動的に設定される。
【関連する外部ページ】
Windsurf の公式ページ: https://windsurf.com/
必要なPythonライブラリのインストール
- Windowsで、コマンドプロンプトを管理者権限で起動する(Windowsキーまたはスタートメニューから「cmd」と入力し、右クリックメニューで「管理者として実行」を選択)。
- 以下のコマンドで必要なライブラリをインストールする。
pip install -U pandas numpy matplotlib japanize-matplotlib scipy
【関連する外部ページ】
【サイト内の関連ページ】
基本的なデータ構造とデータフレームの作成
pandasのデータフレームは、表形式のデータを扱う基本構造である。ここでは成績データを辞書から作成し、データフレームへ変換する。データ型を明示的に指定することで、メモリ使用量の削減と処理速度の向上が期待できる。
- データ作成: 辞書dataに科目、受講者、得点のデータを格納する。
- データフレームの構築: pd.DataFrame(data)でデータフレームに変換する。
- データ型の指定: astype()で「科目」と「受講者」をカテゴリ型に、「得点」を整数型(int32)に変換する。カテゴリ型は、値の種類が限られる列に指定するとメモリ効率が向上する。
import pandas as pd
# データの作成
data = {
'科目': ['国語', '国語', '算数', '算数', '理科'],
'受講者': ['A', 'B', 'A', 'B', 'A'],
'得点': [90, 80, 95, 90, 80]
}
# データフレームの作成
df = pd.DataFrame(data)
# データ型の明示的な指定
df = df.astype({
'科目': 'category',
'受講者': 'category',
'得点': 'int32'
})
print("基本データ:")
print(df)
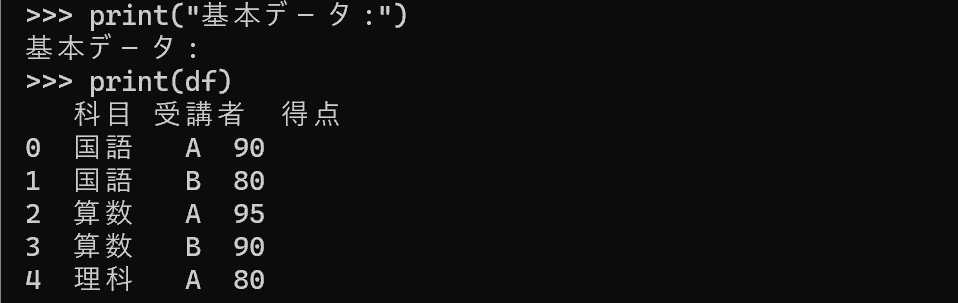
個別の統計量計算
個々の統計量を個別に算出する方法を示す。特定の統計量のみが必要な場合や、計算過程を確認したい場合に有用である。
- 「科目」と「受講者」列をカテゴリ型に、「得点」列を整数型(int32)に変換する。
- 「得点」に対して、平均、標準偏差、中央値、最大値、最小値、四分位数(第1および第3)を算出する。scipyで歪度と尖度を算出する。
- ddof=1を指定して標本標準偏差を算出する。ddof(自由度の調整値)を1に設定すると、標本から母集団の標準偏差を推定する不偏推定量となる。
import pandas as pd
from scipy import stats
# データの作成
data = {
'科目': ['国語', '国語', '算数', '算数', '理科'],
'受講者': ['A', 'B', 'A', 'B', 'A'],
'得点': [90, 80, 95, 90, 80]
}
# データフレームの作成
df = pd.DataFrame(data)
# データ型の明示的な指定
df = df.astype({
'科目': 'category',
'受講者': 'category',
'得点': 'int32'
})
# 基本統計量の個別計算
scores = df['得点']
# 標本標準偏差の計算(ddof=1指定)
print("基本統計量:")
print(f"平均値: {scores.mean():.1f}")
print(f"標準偏差: {scores.std(ddof=1):.1f}")
print(f"中央値: {scores.median():.1f}")
print(f"最大値: {scores.max()}")
print(f"最小値: {scores.min()}")
print(f"第1四分位数: {scores.quantile(0.25):.1f}")
print(f"第3四分位数: {scores.quantile(0.75):.1f}")
print(f"歪度: {stats.skew(scores):.3f}")
print(f"尖度: {stats.kurtosis(scores):.3f}")
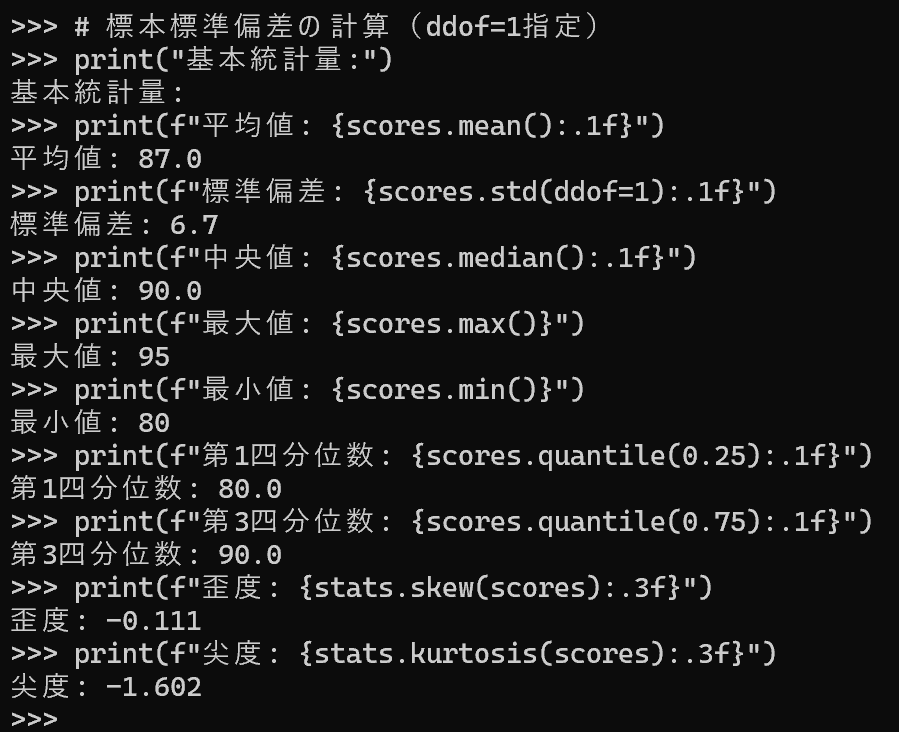
総合的な統計分析
describeメソッドは、主要な記述統計量を一括で算出する。データの概要を素早く把握したい場合に有用である。
- データ型の適正化: 「科目」と「受講者」列をカテゴリ型に、「得点」列を整数型(int32)に変換して処理効率を向上させる。
- 総合分析: describe()メソッドで全体の得点データの基本統計量を一括算出する。
- カテゴリ別分析: groupby()メソッドとdescribe()メソッドを組み合わせ、科目ごとの統計量を算出する。
import pandas as pd
# データの作成
data = {
'科目': ['国語', '国語', '算数', '算数', '理科'],
'受講者': ['A', 'B', 'A', 'B', 'A'],
'得点': [90, 80, 95, 90, 80]
}
# データフレームの作成
df = pd.DataFrame(data)
# データ型の明示的な指定
df = df.astype({
'科目': 'category',
'受講者': 'category',
'得点': 'int32'
})
# describe()メソッドによる総合的な統計量の算出
# count:データ数、mean:平均、std:標準偏差、min:最小値、25%:第1四分位、50%:中央値、75%:第3四分位、max:最大値
print("\n総合的な統計量:")
print(df['得点'].describe())
# 科目別の統計量
# groupby()で科目ごとにグループ化し、describe()で各グループの統計量を算出
print("\n科目別の統計量:")
print(df.groupby('科目')['得点'].describe())
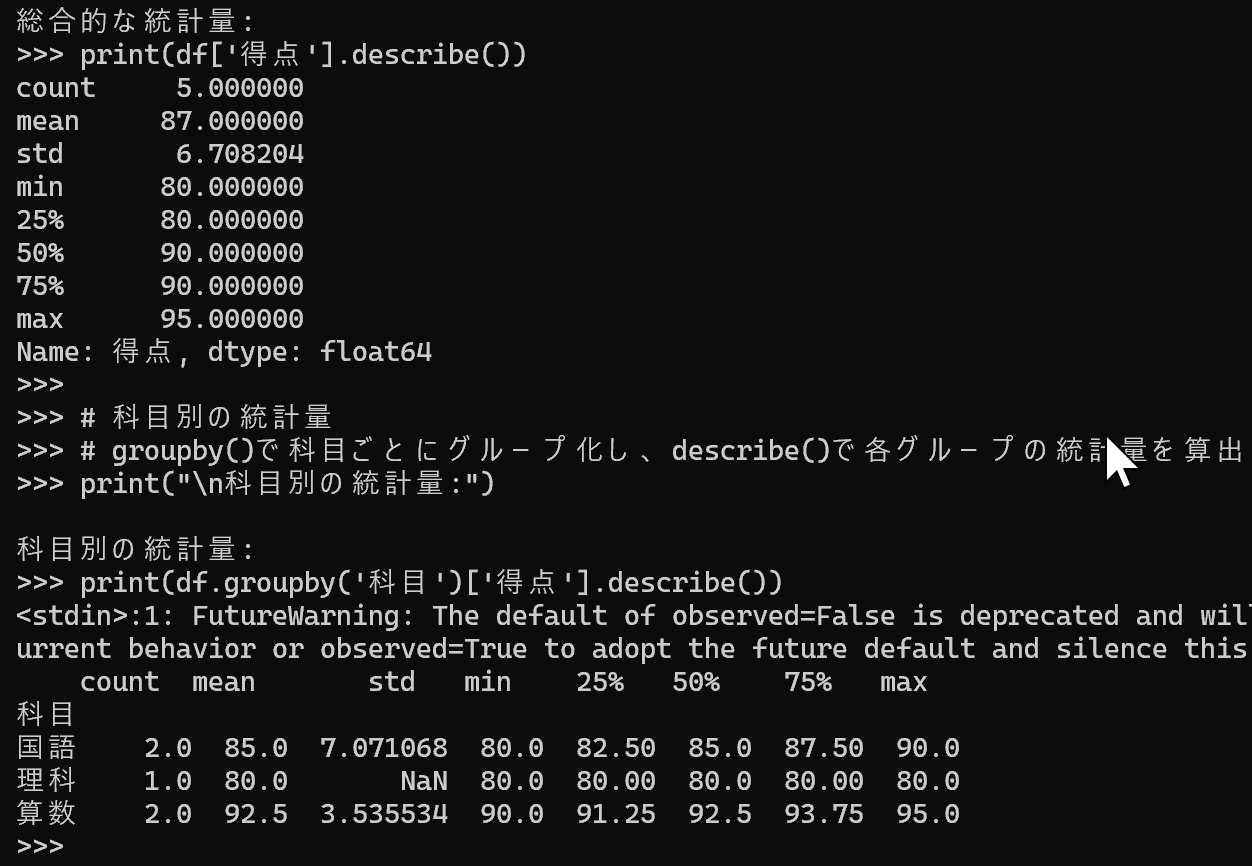
データの可視化(箱ひげ図とヒストグラム)
データの分布を視覚的に把握することで、数値だけでは見えにくい特徴を発見できる。箱ひげ図はグループ間の比較に、ヒストグラムは分布の形状把握に適している。
- 箱ひげ図の生成: pandasのboxplotメソッドで科目ごとの得点分布を可視化する。中央値、四分位数、外れ値を一度に確認できる。
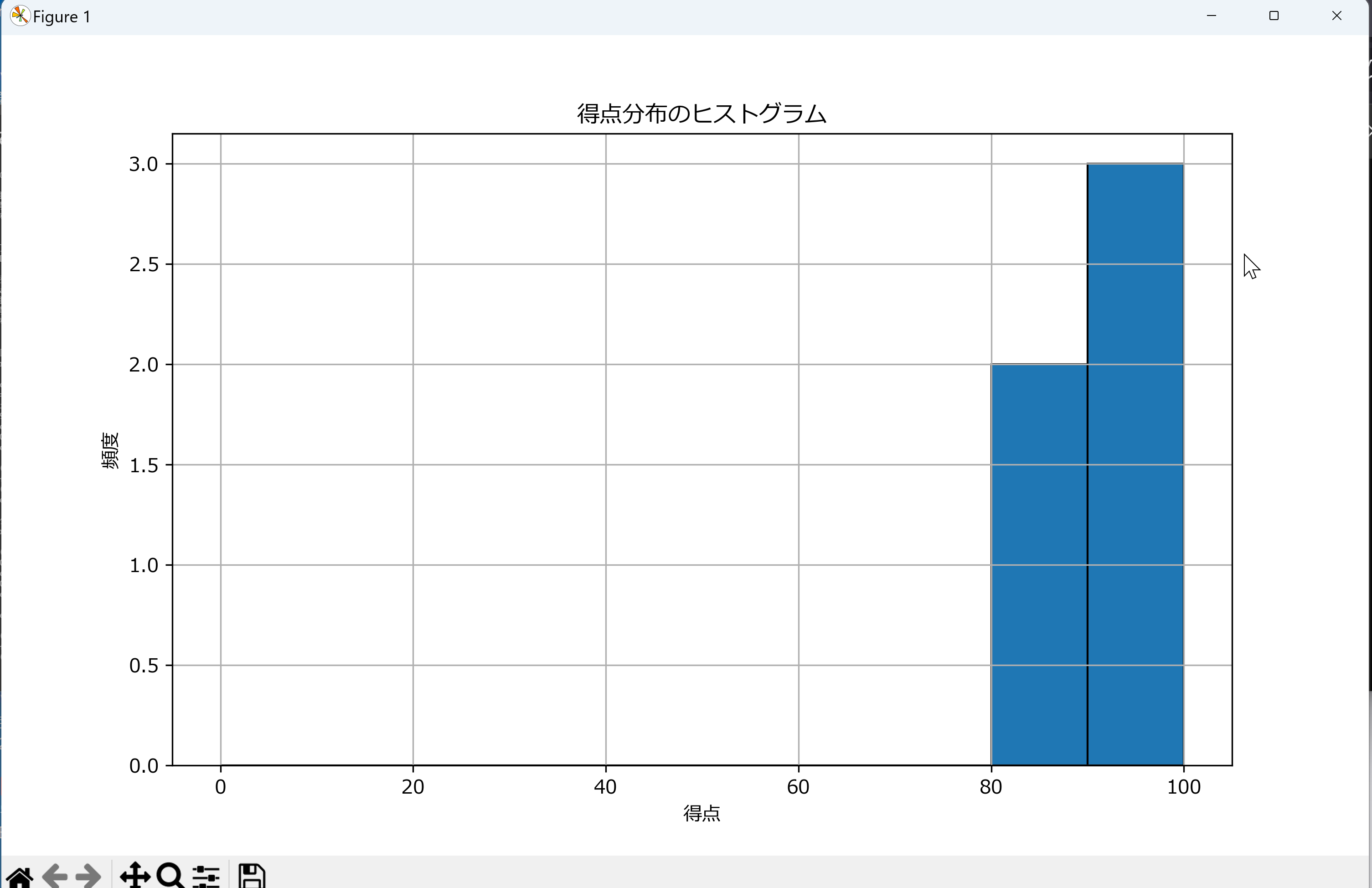
- ヒストグラムの作成: plt.histで得点分布を表示する。binsパラメータで区間幅を指定する。
- 日本語表示: japanize_matplotlibをインポートすると、グラフ内の日本語が正しく表示される。
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib # 日本語表示用
import platform
# OSがWindowsの場合のみフォントを設定
if platform.system() == 'Windows':
plt.rcParams['font.family'] = 'Meiryo'
# データの作成
data = {
'科目': ['国語', '国語', '算数', '算数', '理科'],
'受講者': ['A', 'B', 'A', 'B', 'A'],
'得点': [90, 80, 95, 90, 80]
}
# データフレームの作成
df = pd.DataFrame(data)
# データ型の明示的な指定
df = df.astype({
'科目': 'category',
'受講者': 'category',
'得点': 'int32'
})
# 箱ひげ図の作成
plt.figure(figsize=(10, 6))
df.boxplot(column='得点', by='科目')
plt.suptitle('') # 自動で付加されるサブタイトルを削除
plt.title('科目別得点分布', pad=15) # タイトルの余白調整
plt.ylabel('得点')
plt.grid(True)
plt.savefig('score_distribution.png', bbox_inches='tight') # 画像を保存
plt.show() # 画面に表示
plt.close() # 描画後にクローズ
# ヒストグラムの作成
plt.figure(figsize=(10, 6))
plt.hist(df['得点'], bins=range(0, 101, 10), edgecolor='black') # binの範囲を0-100に設定
plt.title('得点分布のヒストグラム')
plt.xlabel('得点')
plt.ylabel('頻度')
plt.grid(True)
plt.savefig('score_histogram.png', bbox_inches='tight') # 画像を保存
plt.show() # 画面に表示
plt.close() # 描画後にクローズ
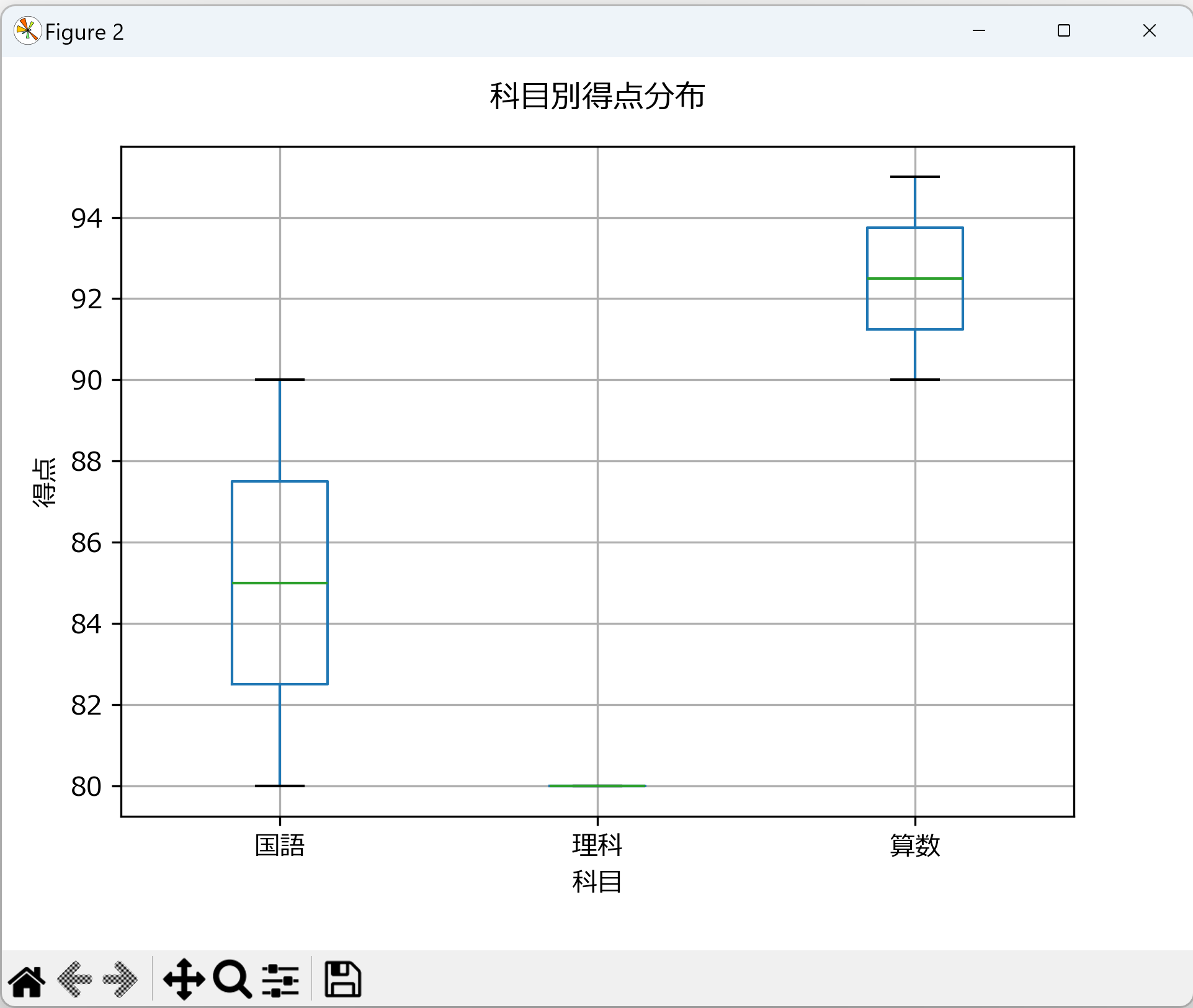
クロス集計表
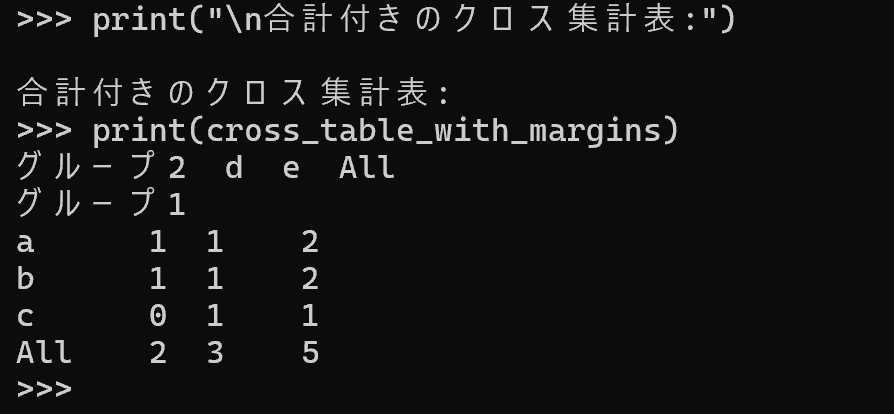
クロス集計表は、2つのカテゴリ変数の組み合わせごとの頻度を表形式で示す。変数間の関連性を把握する際に有用である。
- クロス集計の実装: pd.crosstab関数で「グループ1」を行、「グループ2」を列として、各組み合わせの出現頻度を算出する。
- 合計の表示: margins=Trueを指定すると、行と列の合計が追加される。
import pandas as pd
# データセットサンプルの作成
data = {
'グループ1': ['a', 'b', 'c', 'a', 'b'],
'グループ2': ['d', 'd', 'e', 'e', 'e']
}
df = pd.DataFrame(data)
# クロス集計表の作成
# crosstabは2つの系列間でグループ単位での頻度(出現回数)を集計する
# index=行インデックス, columns=列インデックスを指定
cross_table = pd.crosstab(df['グループ1'], df['グループ2'])
print(cross_table)
# (Optional) 行・列の合計を含めたい場合は、margins=True を指定
cross_table_with_margins = pd.crosstab(df['グループ1'], df['グループ2'], margins=True)
print("\n合計付きのクロス集計表:")
print(cross_table_with_margins)
t検定
t検定は、2群の平均値に統計的に有意な差があるかを判断する手法である。ここでは分散が等しくない場合にも適用できるWelchのt検定を実装する。
- サンプルデータの生成: numpyで正規分布から2群のサンプルデータを生成する。
- 再現性の確保: np.random.seed(42)で乱数のシードを固定すると、同じ結果を再現できる。
- 検定の実施: ttest_ind関数にequal_var=Falseを指定するとWelchのt検定となる。等分散を仮定する通常のt検定より適用範囲が広い。
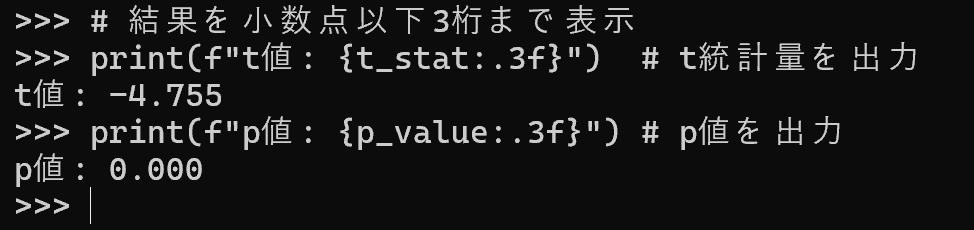
- 結果の解釈: p値が有意水準(通常0.05)未満であれば、2群の平均値に有意な差があると判断する。
import numpy as np
from scipy import stats
# シード値を固定して再現性を確保
np.random.seed(42)
# 2群のサンプルデータを正規分布から生成
# group1: 平均0、標準偏差1の正規分布から100個
# group2: 平均0.5、標準偏差1の正規分布から100個
group1 = np.random.normal(0, 1, 100)
group2 = np.random.normal(0.5, 1, 100)
# Welchのt検定を実行
# equal_var=Falseで分散が等しくないことを仮定
# 戻り値はt統計量とp値のタプル
t_stat, p_value = stats.ttest_ind(group1, group2, equal_var=False)
# 結果を小数点以下3桁まで表示
print(f"t値: {t_stat:.3f}") # t統計量を出力
print(f"p値: {p_value:.3f}") # p値を出力
一元配置分散分析
一元配置分散分析は、3群以上の平均値に差があるかを検定する手法である。t検定は2群間の比較に限られるため、3群以上を同時に比較する場合はこの手法を用いる。
- 分析の実装: scipyのstats.f_oneway()関数で一元配置分散分析を実行する。
- データ構造の準備: 各群の測定値をリストとして準備する。
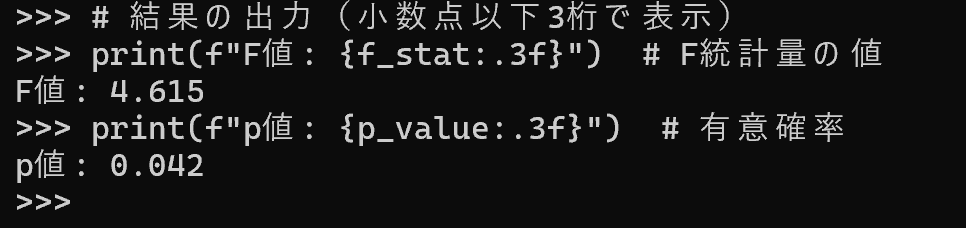
- 結果の解釈: p値が有意水準未満であれば、少なくとも1組の群間に有意な差がある。どの群間に差があるかは、多重比較(事後検定)で調べる。
from scipy import stats
# サンプルデータ(数値のグループ別データ)
group_a = [3.42, 3.84, 3.96, 3.76] # グループAの測定値
group_b = [3.17, 3.63, 3.47, 3.44, 3.39] # グループBの測定値
group_c = [3.64, 3.72, 3.91] # グループCの測定値
# 一元配置分散分析の実行
f_stat, p_value = stats.f_oneway(group_a, group_b, group_c)
# 結果の出力(小数点以下3桁で表示)
print(f"F値: {f_stat:.3f}") # F統計量の値
print(f"p値: {p_value:.3f}") # 有意確率
正規性の検定
Shapiro-Wilk検定は、データが正規分布に従うかを検定する手法である。t検定や分散分析などのパラメトリック検定は正規性を仮定するため、事前にこの検定で確認することが望ましい。
- 検定の実装: scipyのstats.shapiro()関数でShapiro-Wilk検定を実行する。
- データ生成: numpyで正規分布に従う100個のサンプルデータを生成する。
- 再現性の確保: np.random.seed(42)で乱数のシードを固定する。
- 結果の解釈: p値が有意水準(通常0.05)以上であれば、帰無仮説を棄却できず、正規性を否定する根拠がない。ただし、これは正規分布に従うことの証明ではない。p値が有意水準未満であれば、正規分布に従わない可能性が高く、ノンパラメトリック検定の使用を検討する。
from scipy import stats
import numpy as np
# データ生成:平均0、標準偏差1の正規分布から100個のサンプルを生成
np.random.seed(42)
data = np.random.normal(0, 1, 100)
# Shapiro-Wilk検定の実行
# 帰無仮説:データは正規分布に従う
stat, p_value = stats.shapiro(data)
# 結果の出力(小数点以下3桁まで表示)
print(f"検定統計量: {stat:.3f}")
print(f"p値: {p_value:.3f}")
![[kaneko lab.]](https://www.kkaneko.jp/info/logo_png.png)