GSL (GNU Scientific Library) を用いた FFT

GSL の FFT に関する機能について，一部分を紹介する．

GNU Scientific Library -- Reference Manual の 15 章「Fast Fourier Transforms (FFTs)」

前準備

GSL のインストール

Windows での GSL のインストール（ソースコードを使用）（MSYS2，configure，make を利用）: 別ページ »で説明

実数列，半複素数列の FFT

【要点】

実数データに対してFFTを行うと，結果は複素共役対称性を持つ．この対称性を利用して，冗長な部分を省いた形式で格納したものが半複素数列（half-complex sequence）である．半複素数列を使用することで，メモリ使用量を削減できる．

混合基数法は，任意のデータ長に対して使うことができる（長さが2の累乗 (radix 2)でなくても構わないということ）． GSL に実装されている混合基数法は，パウル・シュヴァルツラウバーのFFTPACK ライブラリを実装しなおしたものである．
実数列に FFT を行うと，半複素数列が得られる．この関数が gsl_fft_real_transform である．
gsl_fft_real_transform の出力である半複素数列を，一般的な複素数配列に変換するには，次の関数を使う
```
int gsl_fft_halfcomplex_unpack (const double halfcomplex_coefficient [],
gsl_complex_packed_array complex_coefficient, size_t stride, size_t n)
```
半複素数列は，実部と虚部が交互に格納される形式である．データ長 N = 5 の場合，半複素数列は以下のように格納される．
```
配列インデックス:  0    1    2    3    4
格納される値:     r(0) r(1) i(1) r(2) i(2)

r(k): 周波数成分 k の実部
i(k): 周波数成分 k の虚部
```
ここで，r(0) は直流成分（周波数0）の実部である．実数データのFFTでは直流成分の虚部は常に0となるため省略される．
半複素数列に逆 FFT を行うと実数列が得られる．この関数が gsl_fft_halfcomplex_inverse である．

下の2行は必須

#include<gsl/gsl_fft_real.h>
#include<gsl/gsl_fft_halfcomplex.h>

MSYS2 MINGW64 を実行する
スタートメニューで，「MSYS2」の下の「MSYS2 MINGW64」を選ぶ．

プログラムの準備

#include<stdio.h>
#include<math.h>
#include<gsl/gsl_fft_real.h>
#include<gsl/gsl_fft_halfcomplex.h>

#define N 18
int main (int argc, char **argv)
{
  int i;
  double data[N];

  gsl_fft_real_wavetable * real;
  gsl_fft_halfcomplex_wavetable * hc;
  gsl_fft_real_workspace * w;

  data[0]  = 0.0;
  data[1]  = 0.0;
  data[2]  = 0.0;
  data[3]  = 0.0;
  data[4]  = 0.0;
  data[5]  = 0.0;
  data[6]  = 1.0;
  data[7]  = 1.0;
  data[8]  = 1.0;
  data[9]  = 1.0;
  data[10] = 1.0;
  data[11] = 1.0;
  data[12] = 0.0;
  data[13] = 0.0;
  data[14] = 0.0;
  data[15] = 0.0;
  data[16] = 0.0;
  data[17] = 0.0;

  /* 元データの表示 */
  for (i = 0; i < N; i++) {
      printf ("%d: %e\n", i, data[i]);
  }

  w = gsl_fft_real_workspace_alloc(N);
  real = gsl_fft_real_wavetable_alloc(N);
  gsl_fft_real_transform (data, /* stride */ 1, N, real, w);
  gsl_fft_real_wavetable_free (real);

  /* 変換結果の表示 */
  for (i = 0; i < N; i++) {
      printf ("%d: %e\n", i, data[i]);
  }

  hc = gsl_fft_halfcomplex_wavetable_alloc(N);
  gsl_fft_halfcomplex_inverse (data, 1, N, hc, w);
  gsl_fft_halfcomplex_wavetable_free(hc);

  /* 逆変換結果の表示 */
  for (i = 0; i < N; i++) {
    printf ("%d: %e\n", i, data[i]);
  }

  gsl_fft_real_workspace_free (w);

  return 0;
}

ビルドして実行

gcc -I"C:\gsl\include" -c -o a.o a.c
gcc -L"C:\gsl\lib" -o a.exe a.o -lgsl -lgslcblas
./a.exe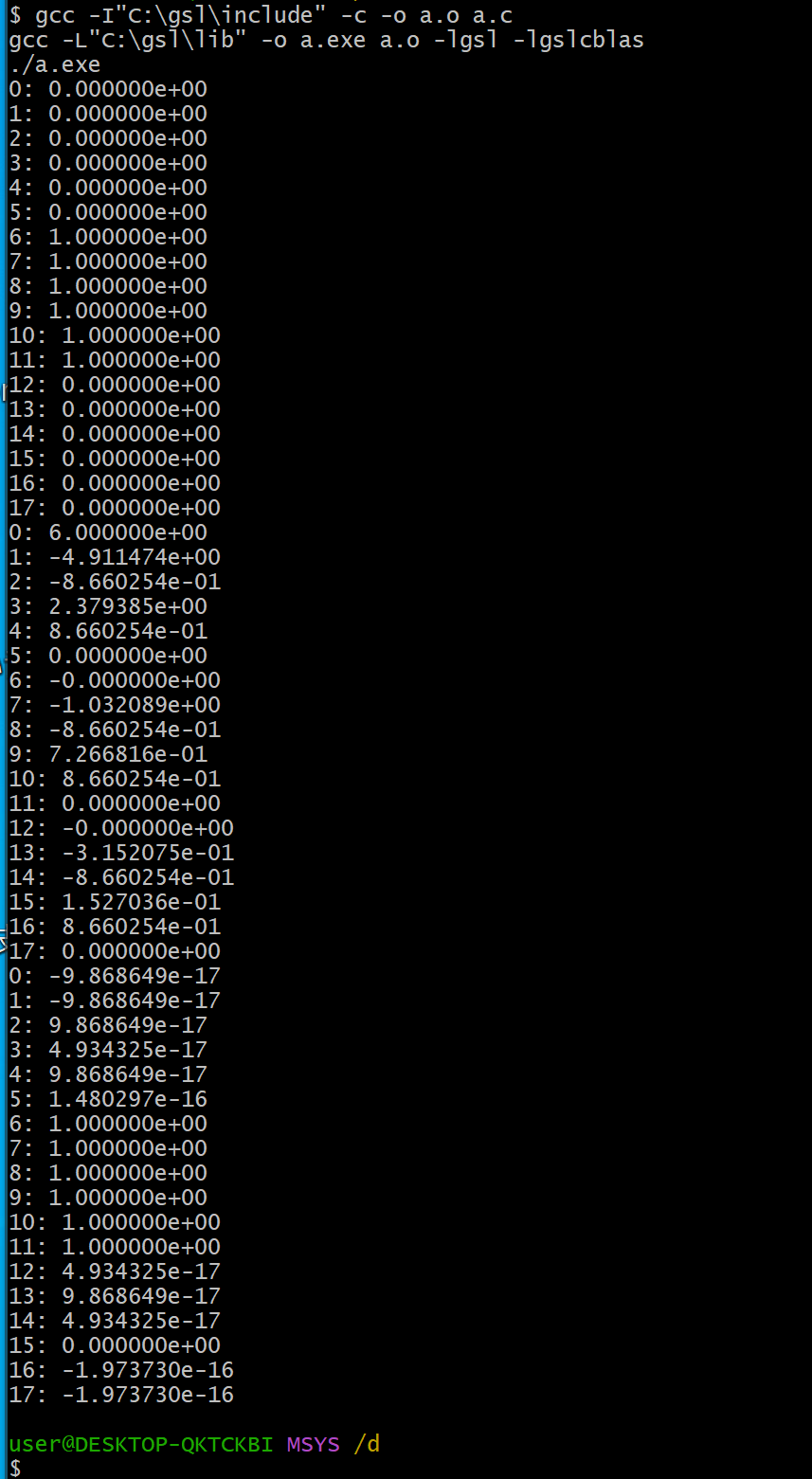

機能まとめ

GSLのFFTでは，波形表（wavetable）と作業領域（workspace）を事前に確保する必要がある．波形表にはFFT計算に必要な三角関数の値が格納され，作業領域には計算中の中間結果が格納される．これらを事前に確保することで，同じデータ長のFFTを繰り返し実行する際の効率が向上する．

実数，半複素数データ FFT用の作業領域の確保（長さが2の累乗 (radix 2)でない場合）
長さ N の実数データの FFT のための作業領域の確保
```
gsl_fft_real_workspace *w = gsl_fft_real_workspace_alloc(N);
```
実数データ FFT用の波形表の確保（長さが2の累乗 (radix 2)でない場合）
```
gsl_fft_real_wavetable *real = gsl_fft_real_wavetable_alloc(N);
```
半複素数 (half-complex) データ FFT用の波形表の確保（長さが2の累乗 (radix 2)でない場合）
```
gsl_fft_halfcomplex_wavetable *hc = gsl_fft_halfcomplex_wavetable_alloc(N);
```
実数データの FFT（長さが2の累乗 (radix 2)でない場合）
作業領域 w, 波形表 real，波形データ data，長さ N，とび数(stride) が１．
```
gsl_fft_real_transform(data, 1, N, real, w);
```
半複素数 (half-complex) データの FFT（長さが2の累乗 (radix 2)でない場合）
作業領域 w, 波形表 hc，波形データ data，長さ N，とび数(stride) が１．
```
gsl_fft_halfcomplex_inverse(data, 1, N, hc, w);
```
実数データ FFT用の波形表の解放（長さが2の累乗 (radix 2)でない場合）
```
gsl_fft_real_wavetable_free(r);
```
半複素数 (half-complex) データ FFT用の波形表の解放（長さが2の累乗 (radix 2)でない場合）
```
gsl_fft_halfcomplex_wavetable_free(hc);
```
実数，半複素数データ FFT用の作業領域の解放（長さが2の累乗 (radix 2)でない場合）
```
gsl_fft_real_workspace_free(w);
```