GSL (GNU Scientific Library) を用いた補間と数値微分

前準備

GSL のインストール

Windows での GSL のインストール（ソースコードを使用）（MSYS2，configure，make を利用）: 別ページ »で説明

補間

1. MSYS2 MINGW64 を実行する

   スタートメニューで，「MSYS2」の下の「MSYS2 MINGW64」を選ぶ．

2. プログラムの準備

   #include<stdio.h>
   #include<math.h>
   #include<gsl/gsl_spline.h>
        
   #define N 8
   int main (int argc, char **argv)
   {
     double x[N], y[N];
     gsl_interp_accel *acc = gsl_interp_accel_alloc();
     gsl_spline *spline = gsl_spline_alloc(gsl_interp_cspline, N); 
     
     /* 三角関数の値を入れる */ 
     int i;
     for(i = 0; i < N; i++) {
       x[i] = (double)i/N; 
       y[i] = sin( x[i] );
     }
   
     // 初期化
     gsl_spline_init(spline, x, y, N);
   
     // 補間
     double xi, yi;
     for(xi = 0; xi < x[N-1];) {
       yi = gsl_spline_eval(spline, xi, acc); 
       fprintf( stderr, "%f, %f\n", xi, yi ); 
       xi = xi + 0.04; 
     }
   
     gsl_spline_free(spline);
     gsl_interp_accel_free(acc);
   
     return 0;
   }
   

3. ビルドして実行

   gcc -I"C:\gsl\include" -c -o a.o a.c
   gcc -L"C:\gsl\lib" -o a.exe a.o -lgsl -lgslcblas
   ./a.exe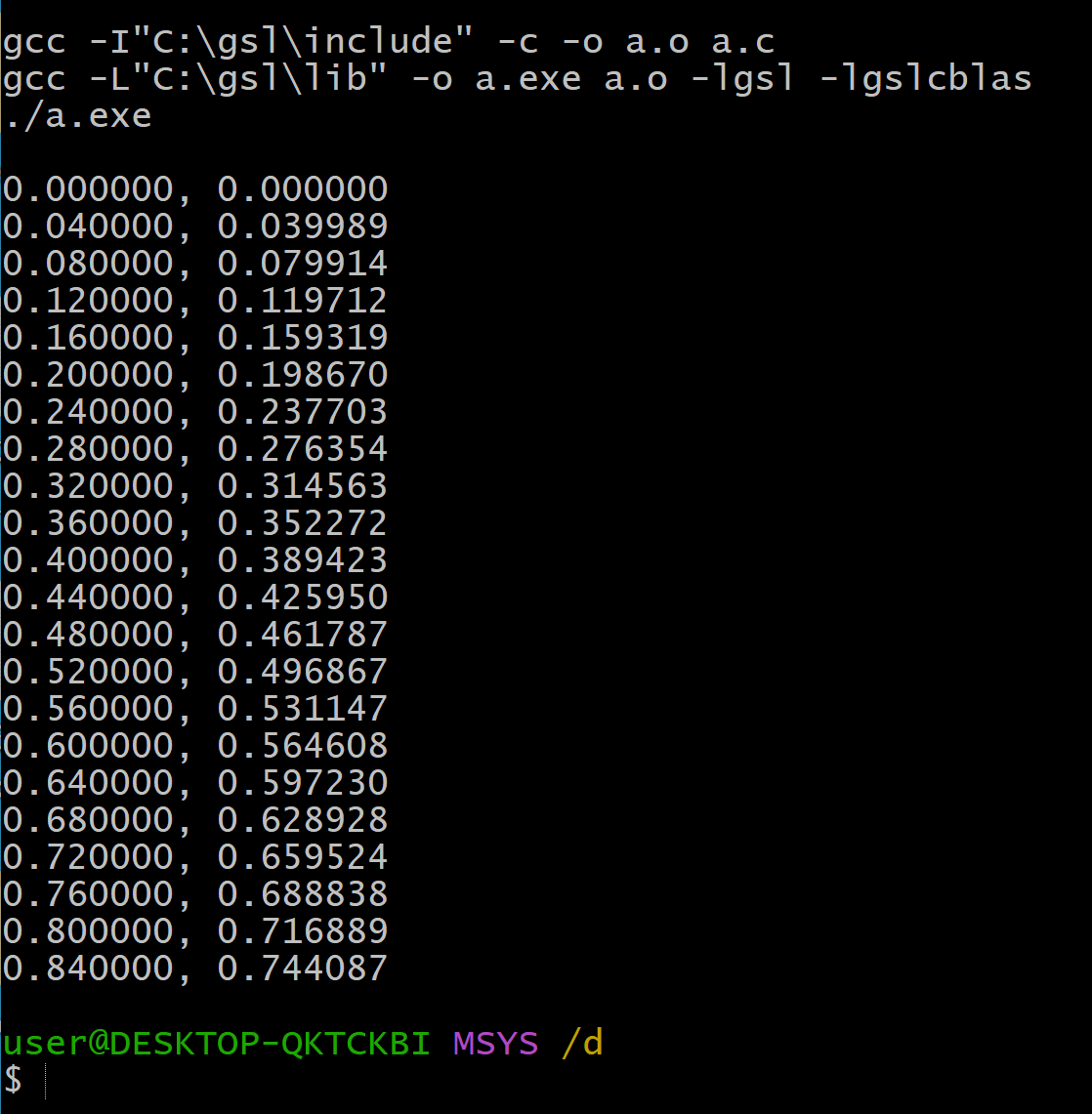
   

   

補間のまとめ

• 加速法を行うためのインスタンスの確保

  gsl_interp_accel *acc = gsl_interp_accel_alloc();
  

• 加速法を行うためのインスタンスの解放

  gsl_interp_accel_free(acc);
  

• gsl_interp インスタンスの確保

  補間法 T，点数が size に対するgsl_interp インスタンスの確保と初期化

  gsl_spline *spline = gsl_spline_alloc(T, size);
  

  T に指定できるもの

  • gsl_interp_linear : 線形補間
  • gsl_interp_polynomial : 多項式補間
  • gsl_interp_cspline : 三次スプライン（自然スプライン）。
  • gsl_interp_cspline_periodic : 周期関数に対する三次スプライン（自然スプライン）。
  • gsl_interp_akima : 秋間スプライン
  • gsl_interp_akima_periodic : : 周期関数に対する秋間スプライン
• gsl_interp インスタンスの解放

  gsl_spline_free(spline);
  

• gsl_interp インスタンスの初期化 spline は gsl_interp インスタンス

  * データ配列 x は整列しておく必要がある．y にはそのような条件はない．

  #define N 100
  ...
  double x[N], y[N];
  ...
  gsl_spline_init(spline, x, y, N);
  

• 補間

  for ( xi=x[0]; xi < x[N-1]; ) {
    yi = gsl_spline_eval(spline, xi, acc);
    xi = xi + 0.1;
    printf( "%d, %d\n", xi, yi );
  }
  

数値微分

1. MSYS2 MINGW64 を実行する

   スタートメニューで，「MSYS2」の下の「MSYS2 MINGW64」を選ぶ．

2. プログラムの準備

   #include<stdio.h>
   #include<gsl/gsl_math.h>
   #include<gsl/gsl_deriv.h>
   
   double f( double x, void* params )
   {
     return sin(x);
   }
   
   int main(int argc, char** argv)
   {
     gsl_function F;
     double result;
     double abserr;
     double x;
     double step;
     F.function = &f;
     F.params = 0;
    
     x = 0.01;
     step = 1e-07;
     gsl_deriv_central(&F, x, step, &result, &abserr);
     fprintf(stderr, "result = %f, abserr = %f\n", result, abserr);
   
     return 0;
   }
   

3. ビルドして実行

   gcc -I"C:\gsl\include" -c -o a.o a.c
   gcc -L"C:\gsl\lib" -o a.exe a.o -lgsl -lgslcblas
   ./a.exe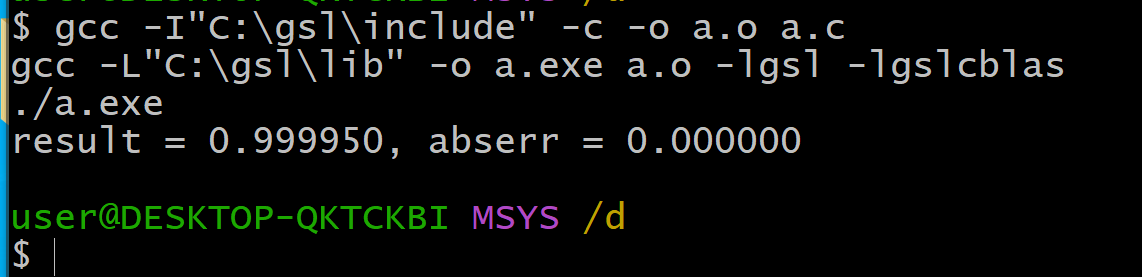
   

   

数値積分のまとめ

• gsl_deriv_central (const gsl_function * f, double x, double h, double * result, double * abserr)

  adaptive central difference アルゴリズムを用いて数値微分を行う．

  • 関数: f
  • 微分を行う点: x
  • ステップサイズ: h
  • 求まった微分値: result
  • 誤差の絶対値 (absolute error): abserr
• gsl_deriv_forward (const gsl_function * f, double x, double h, double * result, double * abserr)

  adaptive forward difference アルゴリズムを用いて数値微分を行う．

  • 関数: f
  • 微分を行う点: x
  • ステップサイズ: h
  • 求まった微分値: result
  • 誤差の絶対値 (absolute error): abserr
• gsl_deriv_backward (const gsl_function * f, double x, double h, double * result, double * abserr)

  adaptive backward difference アルゴリズムを用いて数値微分を行う．

  • 関数: f
  • 微分を行う点: x
  • ステップサイズ: h
  • 求まった微分値: result
  • 誤差の絶対値 (absolute error): abserr