GSL (GNU Scientific Library) のベクトル，行列に関する機能

GSL のベクトル，行列に関する機能について，一部分を紹介する．

最大値，最小値，整列（ソート）
GNU Scientific Library -- Reference Manual の 20 章「Statistics」
乱数
GNU Scientific Library -- Reference Manual の 17 章「Random Number Generation」
乱数の分布
GNU Scientific Library -- Reference Manual の 19 章「Random Number Distributions」
ベクトルと行列
GNU Scientific Library -- Reference Manual の 8 章「Vectors and Matrices」
BLAS
GNU Scientific Library -- Reference Manual の 12 章「BLAS Support」
固有値と固有ベクトル
GNU Scientific Library -- Reference Manual の 14 章「Eigensystems」

前準備

GSL のインストール

Windows での GSL のインストール（ソースコードを使用）（MSYS2，configure，make を利用）: 別ページ »で説明

double の配列に関する最大値，最小値，整列（ソート）

【要点】

C言語の double の配列に対して、 最大値，最小値，整列 などは簡単にできる．
下の1行は必須
```
#include<gsl/gsl_statistics_double.h>
```
飛び幅 (stride)
飛び幅を 1 より大きい値に設定すると、double の配列の中の値を、等間隔で飛び飛びに使う。

MSYS2 MINGW64 を実行する
スタートメニューで，「MSYS2」の下の「MSYS2 MINGW64」を選ぶ．

プログラムの準備

#include<stdio.h>
#include<gsl/gsl_statistics.h>

#define LEN 6

int main(int argc, char** argv)
{
  double data[LEN] = {10.5, 18.2, 10.3, 15.4, 16.2, 18.3};

  double max = gsl_stats_max( data, 1, LEN );
  double min = gsl_stats_min( data, 1, LEN );
  double mean = gsl_stats_mean( data, 1, LEN );
  double sd = gsl_stats_sd( data, 1, LEN );

  printf( "max: \t%f \n", max );
  printf( "min: \t%f \n", min );
  printf( "mean: \t%f \n", mean);
  printf( "sd: \t%f \n", sd );

  return 0;
}

ビルドして実行

gcc -I"C:\gsl\include" -c -o a.o a.c
gcc -L"C:\gsl\lib" -o a.exe a.o -lgsl -lgslcblas
./a.exe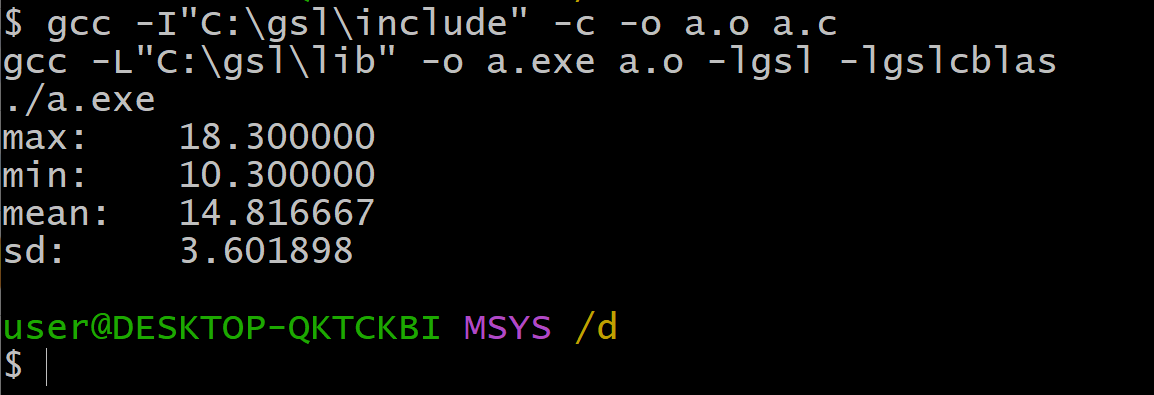

機能まとめ

最大値
データ長 N で，飛び幅 1 のデータセット a の最大値．
```
gsl_stats_max(a, 1, N)
```
最小値
データ長 N で，飛び幅 1 のデータセット a の最小値．
```
gsl_stats_min(a, 1, N)
```
整列
データ長 N で，飛び幅 1 のデータセット a を照準に整列．
```
gsl_sort(a, 1, N);
```
整列
データ長 N で，飛び幅 1 のデータセット a を照準に整列．置換を p に入れる．p は，置換を保持するのに十分な大きさ（つまり，サイズ N）の size_t 型の配列．
元の配列 a は変化しない
```
gsl_sort(p, a, 1, N);
```
上位3個を除き，0 で置き換え．
```
gsl_sort(p, a, 1, N);
for( i = 0; i < N - 3; i++) {
  a[p[i]] = 0.0;
}
```

【関連する外部ページ】

GNU Scientific Library -- Reference Manual の 20 章「Statistics」

乱数発生器

【要点】

下の3行は必須

#include<gsl/gsl_rng.h>
#include<gsl/gsl_randist.h>
#include<gsl/gsl_statistics.h>

MSYS2 MINGW64 を実行する
スタートメニューで，「MSYS2」の下の「MSYS2 MINGW64」を選ぶ．

プログラムの準備

#include<stdio.h>

// この3行は必須
#include<gsl/gsl_rng.h>
#include<gsl/gsl_randist.h>
#include<gsl/gsl_statistics.h>


#define LEN 100

int main(int argc, char** argv)
{
  double a[LEN];
  double b[LEN];

  gsl_rng_env_setup();
  gsl_rng_type *T = (gsl_rng_type *)gsl_rng_default;
  /* 乱数発生器 */
  gsl_rng *r = gsl_rng_alloc(T);
  /* システムクロックを使って乱数の初期値を設定 */
  gsl_rng_set (r, time (NULL));

  int i;
  for(i=0; i<LEN; i++) {
    a[i] =  gsl_rng_uniform(r); 
  }
  for(i=0; i<LEN; i++) {
    b[i] = gsl_ran_gaussian(r, 1.0);
  }

  for(i=0; i<LEN; i++) {
    printf( "%d, \t%7.5f, \t%7.5f \n",
        i, a[i], b[i] );
  }

  printf( "--, \t-------, \t%-------\n") ; 
  printf( "mean: \t%7.5f, \t%7.5f \n",
      gsl_stats_mean(a, 1, LEN), gsl_stats_mean(b, 1, LEN) ); 
  printf( "SD: \t%7.5f, \t%7.5f \n",
      gsl_stats_sd(a, 1, LEN), gsl_stats_sd(b, 1, LEN) );

  gsl_rng_free(r);
}

ビルドして実行

gcc -I"C:\gsl\include" -c -o a.o a.c
gcc -L"C:\gsl\lib" -o a.exe a.o -lgsl -lgslcblas
./a.exe

要点まとめ

乱数発生器
```
  gsl_rng_type *T = (gsl_rng_type *)gsl_rng_default;
  /* 乱数発生器 */
  gsl_rng *r = gsl_rng_alloc(T);
```
上のように書いているので、環境変数 GSL_RNG_TYPE が設定されている場合には，それが乱数発生器として使われる．環境変数 GSL_RNG_TYPE が未定義の場合，乱数発生器として mt19937 (メルセンヌ・ツイスター)が指定されたものとして振舞う．
解放は、gsl_rng_free()関数を使う。
乱数の種 (seed)
gsl_rng_set (r, time (NULL));
time() 関数を使って設定している。
乱数の発生
- 一様分布
  乱数発生器 r を使って，範囲 [0.0, 1.0) の一様分布の乱数を発生．
```
gsl_rng_uniform(r)
```
- ガウス分布
  乱数発生器 r を使って，σ=s のガウス分布の乱数を発生．
```
gsl_ran_gaussian(r, s)
```

double 型の GSL ベクトル

【要点】

ベクトルは，同じデータ型のデータの並び．変数 v に，double 型の要素 2, 3, 4, 1 のベクトル（要素がこの順で並ぶ）を格納したいときは，次のように書く．

gsl_vector *v = gsl_vector_alloc(4); // gsl_vector_alloc() は，double 型の要素を持つ GSL ベクトルの確保．中身は初期化されない．
gsl_vector_set(v, 0, 2.0);
gsl_vector_set(v, 1, 3.0);
gsl_vector_set(v, 2, 4.0);
gsl_vector_set(v, 3, 1.0);
gsl_vector_free(v); // 領域の解放

下の1行は必須

#include<gsl/gsl_vector.h>

ベクトルの領域確保と解放

gsl_vector_double *v = gsl_vector_alloc(4); // gsl_vector_alloc() は，double 型の要素を持つ GSL ベクトルの確保．中身は初期化されない．
gsl_vector_free(v); // 領域の解放

ベクトルの組み立て

要素に値にセット
ベクトル v の第 i 要素を 1.0 にセット．i の値は，0 から，＜ベクトルの長さ−１＞．
```
gsl_vector_set( x, i, 1.0 );
```
全要素を同じ値にセット
ベクトルv の全要素を x にセット．
```
gsl_vector_set_all( v, x );
```
ベクトルの複製
ベクトル src を，ベクトル dest にコピー
```
gsl_vector_memcpy( src, dest );
```

ベクトルの値の取得

要素の取り出し
ベクトルv の第 i 要素を取り出す．i の値は，0 から，＜ベクトルの長さ−１＞．
```
double d = gsl_vector_get( v, i );
```

ベクトルに関する2項演算

要素同士の加算
ベクトル b の要素の値を，ベクトル a の要素に加える (ai <- ai + bi)
```
gsl_vector_add( a, b )
```
要素同士の減算
ベクトル b の要素の値を，ベクトル a の要素から減ずる (ai <- ai - bi)
```
gsl_vector_sub( a, b )
```
要素同士の乗算
ベクトル b の要素の値を，ベクトル a の要素に乗ずる (ai <- ai * bi)
```
gsl_vector_mul( a, b )
```
要素同士の除算
ベクトル b の要素の値を，ベクトル a の要素に除ずる (ai <- ai / bi)
```
gsl_vector_div( a, b )
```
全要素の定数倍
ベクトル v の要素の値を x 倍する (vi <- x * vi)
```
gsl_vector_scale( v, x )
```

集約演算

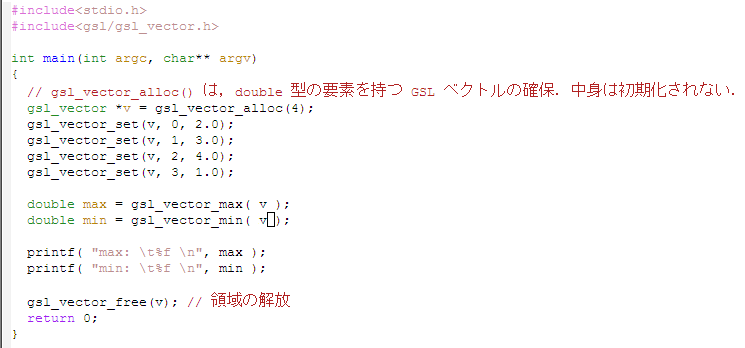
ベクトルの最大値
ベクトル v の最大値を得る
```
double d = gsl_vector_max( v );
```
ベクトルの最小値
ベクトル v の最大値を得る
```
double d = gsl_vector_min( v );
```

ファイル読み出し，書き込み

ファイル (FILE) への，バイナリ形式での読み出し，書き込み
標準出力に，ベクトル v をバイナリ形式で書き込む
```
if ( gsl_vector_fwrite( stdout, v ) != 0 ) {
    fprintf( "error \n" );
}
```
標準入力から，ベクトル v をバイナリ形式で読み出す．
```
if ( gsl_vector_fread( stdin, v ) != 0 ) {
    fprintf( "error \n" );
}
```
ファイル (FILE) への，テキスト形式での読み出し，書き込み
標準出力に，ベクトル v をテキスト形式で書き込む
```
if ( gsl_vector_fprintf( stdout, v, "%f, " ) != 0 ) {
    fprintf( "error \n" );
}
```
標準入力から，ベクトル v をテキスト形式で読み出す．
```
if ( gsl_vector_fscanf( stdin, v, "%f, " ) != 0 ) {
    fprintf( "error \n" );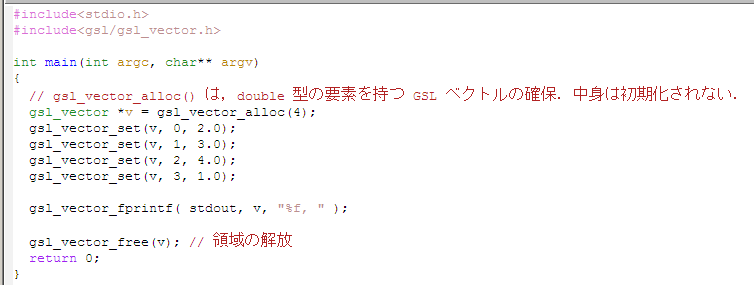
}
```

【関連する外部ページ】

GNU Scientific Library -- Reference Manual の 8 章「Vectors and Matrices」

GSL 行列

【要点】

変数 M に，要素 1, 2, 3, 4 が入った2行2列の行列，つまり， 1 3 2 4 を格納したいときは，次のように書く．「gsl_matrix_alloc(2, 2)」の最初の 2 が行数．次の 2 が列数．

gsl_matrix *M = gsl_matrix_alloc(2, 2); // gsl_matrix_alloc() は，double 型の要素の確保．中身は初期化されない．
gsl_matrix_set(M, 0, 0, 1.0);
gsl_matrix_set(M, 1, 0, 2.0);
gsl_matrix_set(M, 0, 1, 3.0);
gsl_matrix_set(M, 1, 1, 4.0);
gsl_matrix_free(M); // 領域の解放

または

double d = { 1.0, 3.0,
             2.0, 4.0 };
gsl_matrix_view MV = gsl_matrix_view_array( a, 2, 2 );
gsl_matrix v = &MV.matrix

下の1行は必須

#include<gsl/gsl_matrix.h>

ベクトルの領域確保と解放

gsl_matrix *M = gsl_matrix_alloc(2, 2); // gsl_matrix_alloc() は，double 型の要素の確保．中身は初期化されない．
gsl_matrix_free(M); // 領域の解放

行列の組み立て

要素に値にセット
行列 M の第 i 行, 第 j 列の要素を 1.0 にセット．i, j の値は，0 から，行列の縦，横−1．
```
gsl_matrix_set( M, i, j, 1.0 );
```
全要素を同じ値にセット
行列の全要素を x にセット．
```
gsl_matrix_set_all( M, x );
```
単位行列にセット
つまり，対角要素を 1 に，非対角要素を 0 にセットする．行列 M が正方行列でなくても動く．
```
gsl_matrix_set_identity( M );
```
行列の複製
行列 src を，行列 dest にコピー
```
gsl_matrix_memcpy( dest, src );
```

行列の値の取得，ベクトル像の取得

ベクトル像は，ベクトルと同様に扱うことができる．

行の取り出し
行列 M の第 j 行を取り出す．これは参照を使ってベクトル像を生成している．
* gsl_matrix v = &v1.matrix のように書いて，gsl_martix_double へのポインタが得られる
```
gsl_vector_view v1;
v1 = gsl_matrix_row(T, i)
```
列の取り出し
行列 M の第 j 列を取り出す．これは参照を使ってベクトル像を生成している．
* gsl_matrix v = &v1.matrix のように書いて，gsl_martix_double へのポインタが得られる
```
gsl_vector_view v1;
v1 = gsl_matrix_column(T, i)
```
要素の取り出し
行列 M の i 行 j 列の要素を取り出す．i の値は，0 から，＜行列の行数−１＞．j の値は，0 から，＜行列の列−１＞．
```
double d = gsl_matrix_get( v, i, j );
```

ファイル読み出し，書き込み

ファイル (FILE) への，バイナリ形式での読み出し，書き込み
標準出力に，行列 M をバイナリ形式で書き込む
```
if ( gsl_matrix_fwrite( stdout, v ) != 0 ) {
    fprintf( "error \n" );
}
```
標準入力から，行列 M をバイナリ形式で読み出す．
```
if ( gsl_matrix_fread( stdin, v ) != 0 ) {
    fprintf( "error \n" );
}
```
ファイル (FILE) への，テキスト形式での読み出し，書き込み
標準出力に，行列 M をテキスト形式で書き込む
```
if ( gsl_matrix_fprintf( stdout, v, "%f, " ) != 0 ) {
    fprintf( "error \n" );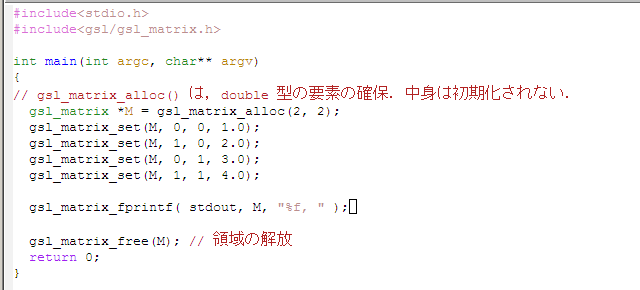
}
```
標準入力から，行列 M をテキスト形式で読み出す．
```
if ( gsl_matrix_fscanf( stdin, v, "%f, " ) != 0 ) {
    fprintf( "error \n" );
}
```

【関連する外部ページ】

GNU Scientific Library -- Reference Manual の 8 章「Vectors and Matrices」

BLAS を呼び出す機能

BLAS(Basic Linear Algebra Subprograms)とは，行列演算，ベクトル演算の機能（下記）をもったプログラム群． GSL には，BLAS の機能を呼び出す機能があります．

Level 1
ベクトルとベクトルの演算
DOT : 内積, AXPY : AXPY 演算 ( y <- ax + y の形など), NORM : ノルム　など
Level 2
行列とベクトルと計算
行列とベクトルの積 ( y <- Ax ), 行列の rank-1 更新 ( A <- A + xy' ) など
Level 3
行列同士の演算
行列と行列の積 ( Z <- XY ) など

GSL ベクトルの内積（ドット積） (Level 1)
GSL ベクトル v1 と v2 の内積（ドット積）．「ddot」の「d」は，GSL ベクトル v1 と v2 が double の精度という意味．
```
#include<gsl_blas.h>
...
double result;
gsl_blas_ddot(v1, v2, &result)
```
GSL ベクトルのノルム (Level 1)
GSL ベクトルv のノルム（ユークリッド距離によるノルム; Euclidean norm）．「dnrm2」の「d」は，GSL ベクトル v が double の精度という意味．
```
#include<gsl_blas.h>
...
double n = gsl_blas_dnrm2(v);
```
GSL ベクトルの要素の総和 (Level 1)
GSL ベクトル v の要素の総和．「dasum」の「d」は，GSL ベクトル v が double の精度という意味．
```
#include<gsl_blas.h>
...
double n = gsl_blas_dasum(v);
```
GSL ベクトルのスカラ倍 (Level 1)
GSL ベクトル v の要素を alpha 倍して，v 二格納．「dscal」の「d」は，GSL ベクトル v が double の精度という意味．
```
#include<gsl_blas.h>
...
double n = gsl_blas_dscal( alpha, v );
```

GSL ベクトルと GSL 行列の積 (Level 2)

y = M x + y

#include<gsl_blas.h>
...
/* y = M x + y */
gsl_blas_dgemv( CblasNoTrans, 1.0, M, x, 1.0, y );

GSL 行列と GSL 行列の積 (Level 3)

C = AB + C

#include<gsl_blas.h>
...
/* C = A B */
gsl_blas_dgemm( CblasNoTrans, CblasNoTrans, 1.0, A, B, 0.0, C );

【関連する外部ページ】:

GNU Scientific Library -- Reference Manual の 12 章「BLAS Support」
https://www.gnu.org/software/gsl/manual/html_node/BLAS-Support.html

固有値，固有ベクトル

【要点】

GSL 固有値，固有ベクトルを計算するには，そのための作業領域確保と解放を行うことが必要．
大きな行列の固有値と固有ベクトルを求める場合には，GSL でなく，LAPACK などを用いるべき，ということが GSL の説明書に書いてある．
下の1行は必須
```
#include<gsl/gsl_eigen.h>
```

実数対称行列

実数対称行列用の作業領域の確保
D × D の実数対称行列の固有値を計算するための作業領域の確保
```
gsl_eigen_symm_workspace *w = gsl_eigen_symm_alloc( D );
```
実数対称行列の固有値
GSL 行列 (gsl_matrix) A の固有値を計算する． A は実数対称行列であること．計算された固有値は，GSL ベクトル (gsl_vector) v に格納される．
実行の結果 A は破壊される．
```
gsl_eigen_symm( A, v, w );
```
実数対称行列用の作業領域の確保
D × D の実数対称行列の固有値と固有ベクトルを計算するための作業領域の確保
```
gsl_eigen_symmv_workspace *w = gsl_eigen_symmv_alloc( D );
```
実数対称行列の固有値と固有ベクトル
GSL 行列 (gsl_matrix) A の固有値と固有ベクトルを計算する． A は実数対称行列であること．計算された固有値は，GSL ベクトル (gsl_vector) v に格納される．計算された固有ベクトルは，GSL 行列 (gsl_matrix) c に列として格納される． v の要素と，c の列は対応する（例えば，vの第一要素は，c の第一列になる）．固有ベクトルは，お互いに直交し，長さが 1 になるように正規化されている．
実行の結果 A は破壊される．
```
gsl_eigen_symmv( A, v, c, w );
```
固有値と固有ベクトルの整列
GSL ベクトル (gsl_vector) v に格納されている固有値と， GSL 行列 (gsl_matrix) c 格納されている固有ベクトルを整列する．
```
gsl_eigen_symmv_sort( v, c, GSL_EIGEN_SORT_ABS_DEC );
```
- GSL_EIGEN_SORT_VAL_ASC 数値の昇順
- GSL_EIGEN_SORT_VAL_DESC 数値の降順
- GSL_EIGEN_SORT_ABS_ASC 絶対値の昇順
- GSL_EIGEN_SORT_ABS_ASC 絶対値の降順
実数対称行列用の作業領域の解放
作業領域の解放
```
gsl_eigne_symmv_free( w );
```

実数非対称行列

実数非対称行列用の作業領域の確保
D × D の実数非対称行列の固有値を計算するための作業領域の確保
```
gsl_eigen_nonsymm_workspace *w = gsl_eigen_nonsymm_alloc( D );
```
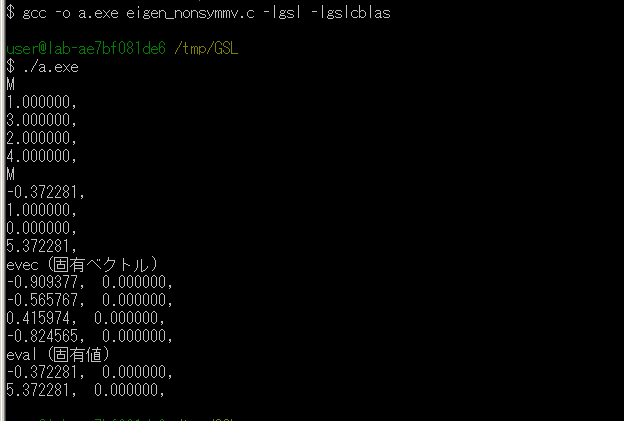
実数非対称行列の固有値
GSL 行列 (gsl_matrix) A の固有値を計算する． A は実数非対称行列．計算された固有値は，GSL 複素数ベクトル (gsl_complex_vector) v に格納される．
実行の結果 A は破壊される．
```
gsl_eigen_nonsymm( A, v, w );
```
実数非対称行列用の作業領域の確保
D × D の実数非対称行列の固有値と固有ベクトルを計算するための作業領域の確保
```
gsl_eigen_nonsymmv_workspace *w = gsl_eigen_nonsymmv_alloc( D );
```
実数非対称行列の固有値と固有ベクトル
GSL 行列 (gsl_matrix) A の固有値と固有ベクトルを計算する． A は実数非対称行列であること．計算された固有値は，GSL 複素数ベクトル (gsl_complex_vector) v に格納される．計算された固有ベクトルは，GSL 複素数行列 (gsl_complex_matrix) c に列として格納される． v の要素と，c の列は対応する（例えば，vの第一要素は，c の第一列になる）．固有ベクトルは，お互いに直交し，長さが 1 になるように正規化されている．
実行の結果 A は破壊される．
```
gsl_eigen_nonsymmv( A, v, c, w );
```
固有値と固有ベクトルの整列
GSL ベクトル (gsl_vector) v に格納されている固有値と， GSL 行列 (gsl_matrix) c 格納されている固有ベクトルを整列する．
```
gsl_eigen_nonsymmv_sort( v, c, GSL_EIGEN_SORT_ABS_DEC );
```
- GSL_EIGEN_SORT_VAL_ASC 数値の昇順
- GSL_EIGEN_SORT_VAL_DESC 数値の降順
- GSL_EIGEN_SORT_ABS_ASC 絶対値の昇順
- GSL_EIGEN_SORT_ABS_ASC 絶対値の降順
実数非対称行列用の作業領域の解放
作業領域の解放
```
gsl_eigne_nonsymmv_free( w );
```

【関連する外部ページ】

GNU Scientific Library -- Reference Manual の 14 章「Eigensystems」