濃淡画像のフーリエ変換と低域／高域通過フィルタ

前準備

Octave のインストール

Windows での Octave のインストールは，別ページ »で説明
Ubuntu での Octave のインストールは，別ページ »で説明

説明

このページでは「画素値」，「濃淡画像」という言葉を次の意味で使う．

画素値
画素値は実数であり，大きな値や負の値をとることがある．表示したときには，画素値の０が黒で表示され，画素値の１が白で表示される．０より小さな値，１を超える値は正しく表示されない．画像ファイルにおいて，画素の諧調は，普通０から２５５の１バイトの数値で表現されていることが多い．このページでは読み込みの時点において，２５５で割ることにする．
濃淡画像
濃淡画像とは，画素値の行列である．

このページでは，次の Octave の関数を使う

画像ファイルの読み込み: imread 関数
カラー画像の濃淡化: rgb2gray 関数
画像ファイルの表示（カラーマップを使用）: imshow 関数
最大値，最小値，平均値，標準偏差: max, min, mean, std 関数
Blackman 窓関数のフィルタ係数: blackman 関数
2 次元の FFT: fft2 関数
2 次元の逆FFT: ifft2 関数
FFT の結果で直流成分が中央に来るようにシフト: fftshift 関数

この Web ページのプログラムでは，変数を次の意味で使う．

A: 濃淡画像のデータ

カラー画像ファイルの読み込み，濃淡画像の表示とのファイル書き出し

カラー画像ファイルは imread 関数で読み込む．rgb2gray 関数を使い濃淡値に変換する．この時点では 0 から 255 の値をとる．256 で割り A に格納する．ここでは，ファイル名 t:/lena_std.jpg を指定してファイルを読み込みます．

* ここでは JPEG ファイルを使っていますが，たいていの種類の画像ファイルを扱うことができる．

pkg load image;

# カラー画像ファイルの読み込みと濃淡画像への変換
[rgb, immap, alpha] = imread("/tmp/lena_std.jpg");
A = double(rgb2gray(rgb))/255;

# 濃淡画像の表示
colormap(gray(256));
imshow(A);

# 濃淡画像のファイル書き出し
imwrite(A, "A.png");

【実行結果の例】

濃淡画像の最大値，最小値，平均値，標準偏差の取得

function [ma, mi, me, st] = grayimage_stat (image)
  # 濃淡画像の最大値，最小値，平均値，標準偏差の取得
  d = reshape( double(image), 1, size(image)(1)*size(image)(2) );
  ma = max(d);
  mi = min(d);
  me = mean(d);
  st = std(d);
endfunction

function disp_grayimage_stat (image, s)
  # 濃淡画像の最大値，最小値，平均値，標準偏差を表示
  # 「濃淡画像」は 0 = 黒，1 = 白である場合，そのまま表示すると分かりづらい．
  # それぞれの値を s 倍する
  [maxImage, minImage, meanImage, stdImage] = grayimage_stat(image);
  disp "max"
  maxImage * s
  disp "min"
  minImage * s
  disp "mean"
  meanImage * s
  disp "std"
  stdImage * s
endfunction

# 濃淡画像 A がセット済みであること
disp_grayimage_stat(A, 255);

【実行結果の例】

フーリエ変換

fft2 関数を使って 2次元の FFT を行う．
fft2 関数の結果として得られる行列の中央に直流成分が来るように fftshift 関数を使ってシフトする（その方が見やすい）．
フーリエ変換の結果を画像に保存するが，単純に表示するとみづらいので log を使って見やすくする．

function logM = log_mat(M)
  # まず，対数を使ったマッピング．
  # 例えば M が 0.001 から 100 の範囲にあるとき,
  # M の値を log(0.001) - log(0.001) / log(100) - log(0.001) から
  # log(100) - log(0.001) / log(100) - log(0.001) にマッピングする．
  # つまり 0 から 1 の範囲になるようにマッピングする．
  MI = min(min(M));
  MA = max(max(M));
  if ( MI < 0.000000001 )
    # too small
    MI = 0.000000001;
  end
  #
  logM = ( log(M) - log(MI) ) / (log(MA) - log(MI));
endfunction


# 濃淡画像 A がセット済みであること
AA = fftshift( fft2( A ) );
imshow(log_mat(abs(real(AA))));
imshow(log_mat(abs(imag(AA))));
imwrite( log_mat(abs(real(AA))), "AAreal.png");
imwrite( log_mat(abs(imag(AA))), "AAimag.png");

【実行結果の例】

実部の画像

虚部の画像

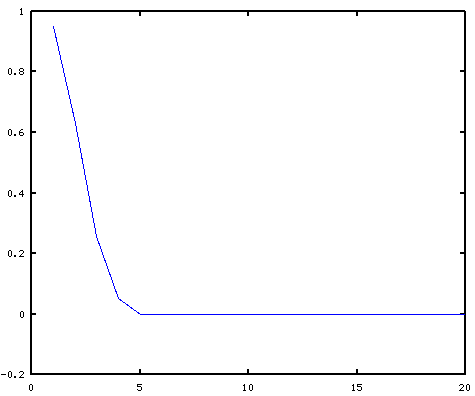
低域／高域通過フィルタのための窓関数

ここでは窓関数を 2次元の行列に格納し，FFT 結果を組み合わせることができるようにします．

function f = get_blackman(N, totallen)
  # blackman 関数を用いて Blackman 窓関数のフィルタ係数を得る

  # 最初に長さ totallen のベクトルを作る（大きめに作るということ）
  f = zeros(1,totallen);
  # 先頭 ceil(N/2) 個だけ値を埋める
  a = blackman(N * 2);
  f([1:N]) = a([N:-1:1]);
endfunction

function F2D = imagefilter(f, xsize, ysize)
  # f はフィルタを表現したベクトル．
  # f(1) は直流成分．f(2), f(3),... と続くにつれ、周波数が上がる
  # これを 2 次元に広げる
  # xsize = 512, ysize = 512 のとき F2D(257,257) に直流成分がくる
  # ずれているように見えるだろうが、これが fftshift の流儀
  [X,Y] = meshgrid( 1:xsize, 1:ysize );
  XX = abs(X - (xsize/2) - 1);
  YY = abs(Y - (ysize/2) - 1);
  F2D = f( max(XX,YY) + 1 );
end

fu = get_blackman(5,20)
plot(fu);

F2D = imagefilter( get_blackman(5,20), 16, 16 );
surfl(F2D);

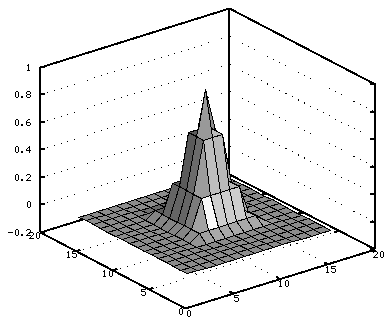
画像の低域／高域通過フィルタ

function Image = apply_grayimage_filter(CC, f)
  # 画像フィルタを得る．
  # f はフィルタ係数を格納したベクトル．
  # f(1) は直流成分．f(2), f(3),... と続くにつれ、周波数が上がる
  # CC は濃淡画像に2次元の FFT を行った結果（複素数の行列）
  # ifft2 は 2 次元の逆 FFT
  Image = real( ifft2( fftshift( CC .* imagefilter( f, size(CC)(1), size(CC)(2) ) ) ) );
endfunction

# AA には，濃淡画像に2次元の FFT を行った結果（複素数の行列）が格納済みであること
# 低域通過フィルタ
U = apply_grayimage_filter(AA, get_blackman(50,2000));
# 高域通過フィルタ
V = apply_grayimage_filter(AA, (1 - get_blackman(50,2000)));
# 濃淡画像の表示とファイル書き出し
# U, V の値の範囲が 0,1 をはみ出すかもしれないので調整
disp_grayimage_stat (U, 255)
disp_grayimage_stat (V, 255)
imshow(min(max(0,U),1));
imwrite(min(max(0,U),1), "U.png");
# キーが押されるのを待つ
disp "please press key"
pause;
imshow(min(max(0,V),1));
imwrite(min(max(0,V),1), "V.png");
# キーが押されるのを待つ
disp "please press key"
pause;
# 再度，2 次元の逆 FFT を実行（バグがないか，2 次元の逆 FFT の結果をみて確認したい）
UU = fftshift( fft2( U ) );
VV = fftshift( fft2( V ) );
imwrite( log_mat(abs(real(UU))), "UUreal.png");
imwrite( log_mat(abs(imag(UU))), "UUimag.png");
imwrite( log_mat(abs(real(VV))), "VVreal.png");
imwrite( log_mat(abs(imag(VV))), "VVimag.png");

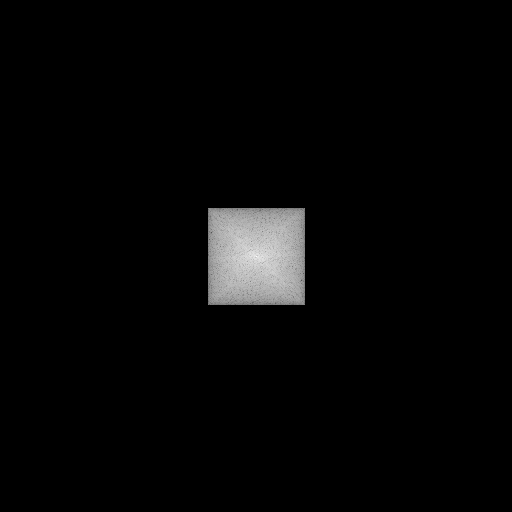
低域通過画像

低域通過画像の 2次元 FFT 結果の実部

低域通過画像の 2次元 FFT 結果の虚部

高域通過画像

高域通過画像の 2次元 FFT 結果の実部

高域通過画像の 2次元 FFT 結果の虚部

disp "sum(sum(abs( AA )))"
sum(sum(abs( AA )))
disp "sum(sum(abs( UU )))"
sum(sum(abs( UU )))
disp "sum(sum(abs( VV )))"
sum(sum(abs( VV )))

surfl( log(abs( AA )) );
surfl( log(abs( UU )) );
surfl( log(abs( VV )) );

ヒストグラム平坦化の例

# histogram euqalization

Ahisteq = histeq( A );
Uhisteq = histeq( U );
Vhisteq = histeq( V );

imwrite(Ahisteq, "Ahisteq.png", 256)
imwrite(Uhisteq, "Uhisteq.png", 256)
imwrite(Vhisteq, "Vhisteq.png", 256)

disp "sum(sum(abs(fftshift( fft2( double(Ahisteq) ) ))))"
sum(sum(abs(fftshift( fft2( double(Ahisteq) ) ))))
disp "sum(sum(abs(fftshift( fft2( double(Uhisteq) ) ))))"
sum(sum(abs(fftshift( fft2( double(Uhisteq) ) ))))
disp "sum(sum(abs(fftshift( fft2( double(Vhisteq) ) ))))"
sum(sum(abs(fftshift( fft2( double(Vhisteq) ) ))))

元画像にヒストグラム平坦化を行った結果

低域通過画像にヒストグラム平坦化を行った結果

高域通過画像にヒストグラム平坦化を行った結果

平均と標準偏差の正規化

[maxA, minA, meanA, stdA] = grayimage_stat(A);
[maxU, minU, meanU, stdU] = grayimage_stat(U);
[maxV, minV, meanV, stdV] = grayimage_stat(V);

Auni = max(0, A / stdA * 0.2 + 0.5 - (meanA / stdA) * 0.2);
Uuni = max(0, U / stdU * 0.2 + 0.5 - (meanU / stdU) * 0.2);
Vuni = max(0, V / stdV * 0.2 + 0.5 - (meanV / stdV) * 0.2);

imwrite(Auni, "Auni.png", 256)
imwrite(Uuni, "Uuni.png", 256)
imwrite(Vuni, "Vuni.png", 256)

disp "sum(sum(abs(fftshift( fft2( double(Auni) ) ))))"
sum(sum(abs(fftshift( fft2( double(Auni) ) ))))
disp "sum(sum(abs(fftshift( fft2( double(Uuni) ) ))))"
sum(sum(abs(fftshift( fft2( double(Uuni) ) ))))
disp "sum(sum(abs(fftshift( fft2( double(Vuni) ) ))))"
sum(sum(abs(fftshift( fft2( double(Vuni) ) ))))

元画像に平均と標準偏差の正規化を行った結果

低域通過画像に平均と標準偏差の正規化を行った結果

高域通過画像に平均と標準偏差の正規化を行った結果

# band pass

w1 = fftshift( fft2( double(mono)  / 255 ) ) ;
for n = 1:512
  for m = 1:512
  x = abs(n-257);
  y = abs(m-257);
  # high pass
  w1(n,m) = w1(n,m) * ( 1 - F( max(x,y) + 1 ) );
  # lowpass
  if ( max(x,y) > 250 )
    w1(n,m) = 0;
  end;
  end;
end;

w2 = fftshift( fft2( double(mono)  / 255 ) ) ;
for n = 1:512
  for m = 1:512
  x = abs(n-257);
  y = abs(m-257);
  # high pass
  w2(n,m) = w2(n,m) * ( 1 - F( max(x,y) + 1 ) );
  # lowpass
  if ( max(x,y) > 210 )
    w2(n,m) = 0;
  end;
  end;
end;

w3 = fftshift( fft2( double(mono)  / 255 ) ) ;
for n = 1:512
  for m = 1:512
  x = abs(n-257);
  y = abs(m-257);
  # high pass
  w3(n,m) = w3(n,m) * ( 1 - F( max(x,y) + 1 ) );
  # lowpass
  if ( max(x,y) > 170 )
    w3(n,m) = 0;
  end;
  end;
end;

w4 = fftshift( fft2( double(mono)  / 255 ) ) ;
for n = 1:512
  for m = 1:512
  x = abs(n-257);
  y = abs(m-257);
  # high pass
  w4(n,m) = w4(n,m) * ( 1 - F( max(x,y) + 1 ) );
  # lowpass
  if ( max(x,y) > 130 )
    w4(n,m) = 0;
  end;
  end;
end;

w5 = fftshift( fft2( double(mono)  / 255 ) ) ;
for n = 1:512
  for m = 1:512
  x = abs(n-257);
  y = abs(m-257);
  # high pass
  w5(n,m) = w5(n,m) * ( 1 - F( max(x,y) + 1 ) );
  # lowpass
  if ( max(x,y) > 90 )
    w5(n,m) = 0;
  end;
  end;
end;

ww1 = histeq( real(ifft2( fftshift(w1) )), 256);
ww2 = histeq( real(ifft2( fftshift(w2) )), 256);
ww3 = histeq( real(ifft2( fftshift(w3) )), 256);
ww4 = histeq( real(ifft2( fftshift(w4) )), 256);
ww5 = histeq( real(ifft2( fftshift(w5) )), 256);

imwrite(ww1, "ww1.png")
imwrite(ww2, "ww2.png")
imwrite(ww3, "ww3.png")
imwrite(ww4, "ww4.png")
imwrite(ww5, "ww5.png")

# FFT again
ww1fft = fftshift( fft2( double(ww1) ) );
ww2fft = fftshift( fft2( double(ww2) ) );
ww3fft = fftshift( fft2( double(ww3) ) );
ww4fft = fftshift( fft2( double(ww4) ) );
ww5fft = fftshift( fft2( double(ww5) ) );

disp "sum(sum(abs(ww1fft)))"
sum(sum(abs(ww1fft)))
disp "sum(sum(abs(ww2fft)))"
sum(sum(abs(ww2fft)))
disp "sum(sum(abs(ww3fft)))"
sum(sum(abs(ww3fft)))
disp "sum(sum(abs(ww4fft)))"
sum(sum(abs(ww4fft)))
disp "sum(sum(abs(ww5fft)))"
sum(sum(abs(ww5fft)))

位相画像

フーリエ変換の後、振幅を１に正規化。その後、逆フーリエ変換

プログラム例

pkg load image;

[rgb, immap, alpha] = imread("fruits.jpg");
mono = rgb2gray( rgb );

colormap(gray(256));
imshow(mono);

mono2 = real( ifft2( fft2(mono) ./ abs( fft2(mono) ) ) );
imshow( 255.0 * mono2 / max(max(mono2)) ); 

mono3 = imsmooth(mono, "Gaussian", sigma=6);
imshow(mono3); 

mono4 = real( ifft2( fft2(mono3) ./ abs( fft2(mono3) ) ) );
imshow( 255.0 * mono4 / max(max(mono4)) );