Octave 7.2.0 のインストール（Windows 上）

Windows での，Octave のインストール手順と，いくつかの代表的な計算（主成分分析など）をスクリーンショット等で説明する． Octaveは，「MATLAB にほぼ互換」ともいわれるプログラミング言語．

【目次】

【サイト内の関連ページ】

先人に感謝．

ダウンロードとインストール

ウェブページを開く

最新の64ビット版のインストーラを選ぶ

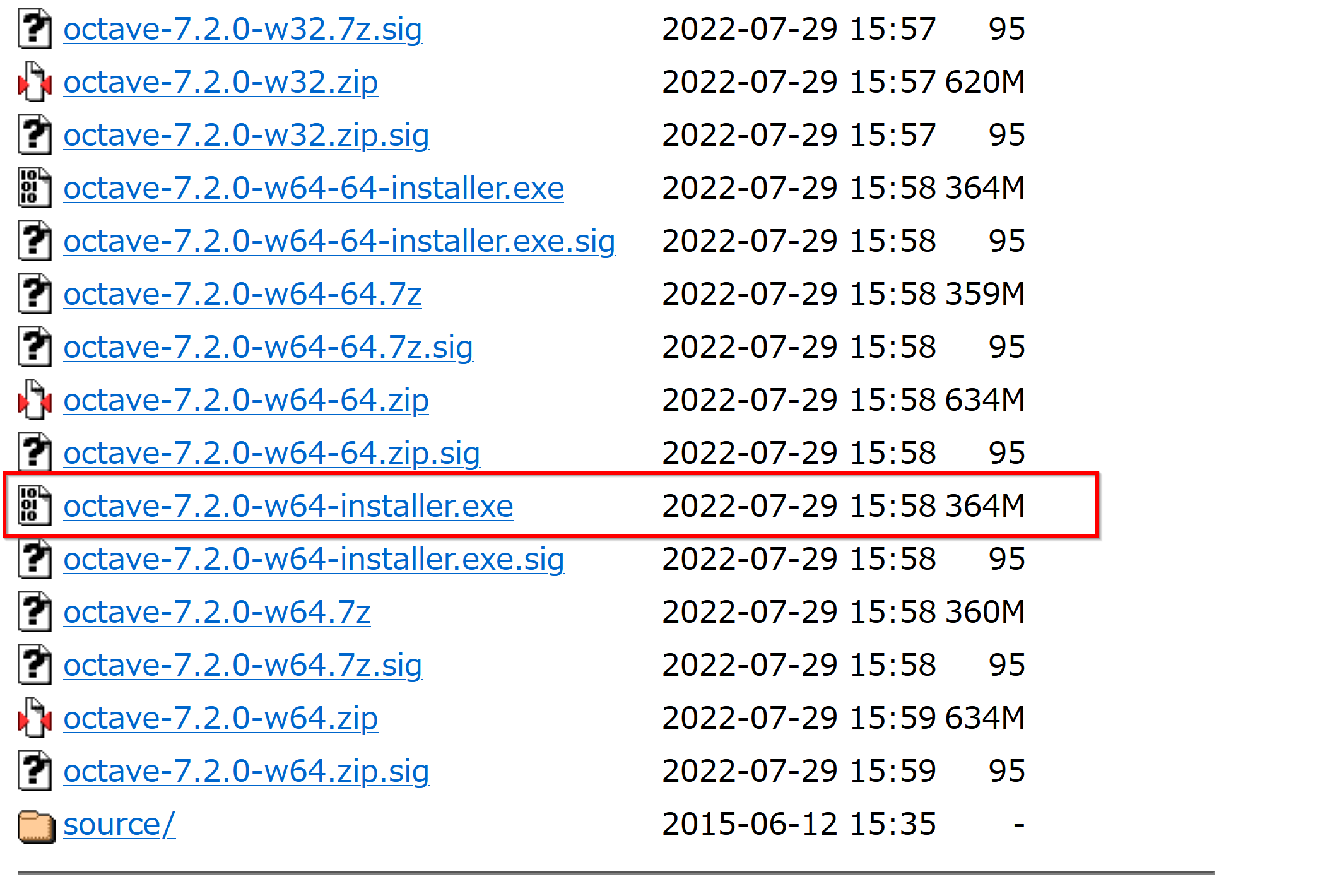
ダウンロードが始まる

ダウンロードした .exe ファイルを実行

ようこそ画面では「Next」をクリック

ライセンス条項の確認．同意できる場合のみ「Next」をクリックすること．

インストールオプションは，既定（デフォルト）のままでよい．「Next」をクリック．

次のインストールオプションは，既定（デフォルト）のままでよい．「Next」をクリック．

インストールディレクトリ（フォルダ）は，既定（デフォルト）のままでよい．「Install」をクリック．

インストールが始まる．

インストール完了の確認．「Finish」をクリック．

試しに起動してみる．

初回起動時には次のような確認画面が開く

試しに使ってみる

X = rand(2000);
Y = rand(2000);
tic(); Z = X * Y; toc();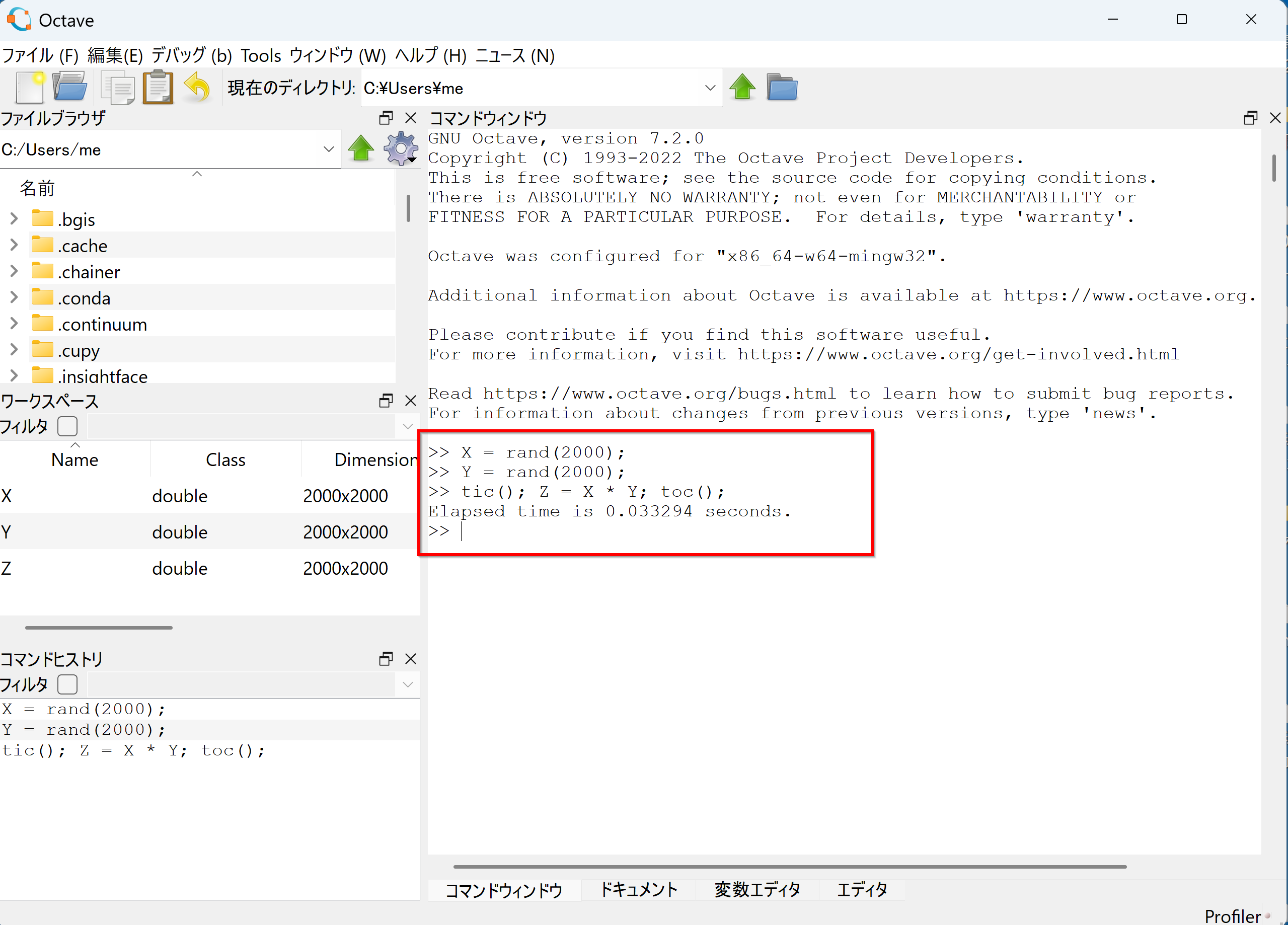

Octave を使ってみる

行列と行列の積: Z = X * Y

LU 分解 (LU decomposition): [L, U, P] = lu(X)

正方行列の逆行列: [Z, RCOND] = inv(X)

行列式 (determinant): [D, RCOND] = det(X)

Singular Value Decomposition (SVD): [U, S, V] = svd(X)

QR factorization (QR decomposition ともいう): [Q, R, P] = qr(X)

分散共分散行列: Z = cov(X, Y)

分散共分散行列の固有値と固有ベクトル（主成分分析）: [v, L] = eig( cov(X) )

princomp 関数による主成分分析: [pc, z, w, Tsq] = princomp(X)

2次元の畳み込み（コンボリューション）: Z = conv2(X, B, 'full')

2次元の高速フーリエ変換 (FFT): Z = fft2(X, 2000, 2000)

convex hull: H = convhull(x, y)

【実測値の例】

[image]
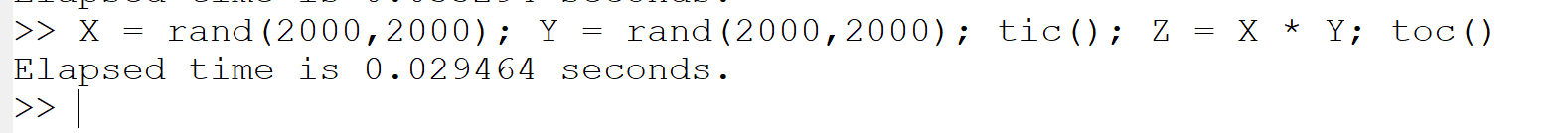
(a) 行列と行列の積:
X = rand(2000,2000); Y = rand(2000,2000); tic(); Z = X * Y; toc()

[image]
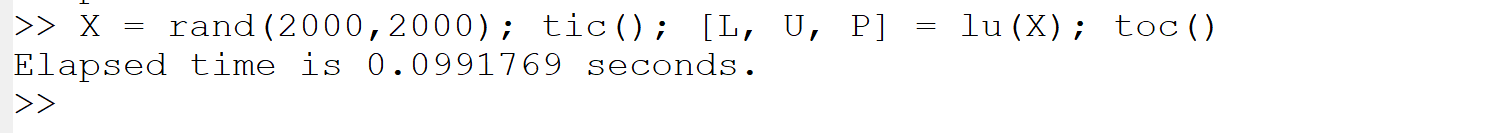
(b) LU 分解 (LU decomposition):
X = rand(2000,2000); tic(); [L, U, P] = lu(X); toc()

[image]
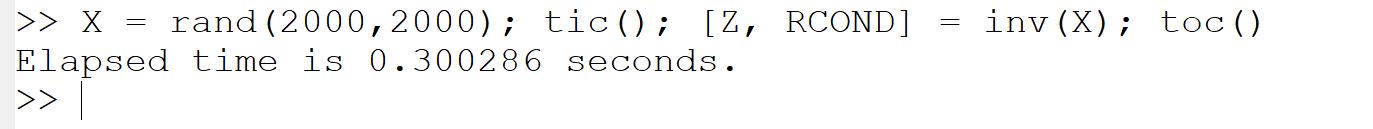
(c) 正方行列の逆行列:
X = rand(2000,2000); tic(); [Z, RCOND] = inv(X); toc()

[image]
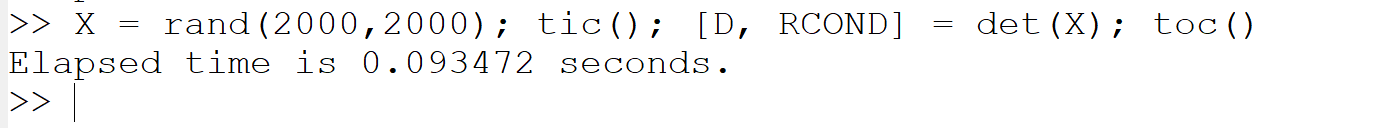
(d) 行列式 (determinant):
X = rand(2000,2000); tic(); [D, RCOND] = det(X); toc()

[image]
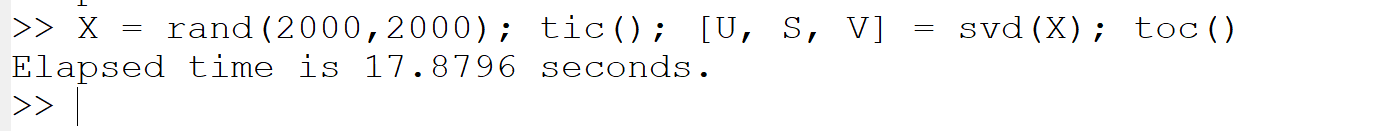
(e) Singular Value Decomposition (SVD):
X = rand(2000,2000); tic(); [U, S, V] = svd(X); toc()

[image]
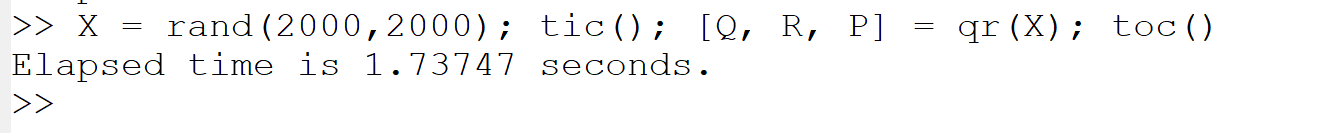
(f) QR factorization (QR decomposition ともいう):
X = rand(2000,2000); tic(); [Q, R, P] = qr(X); toc()

[image]
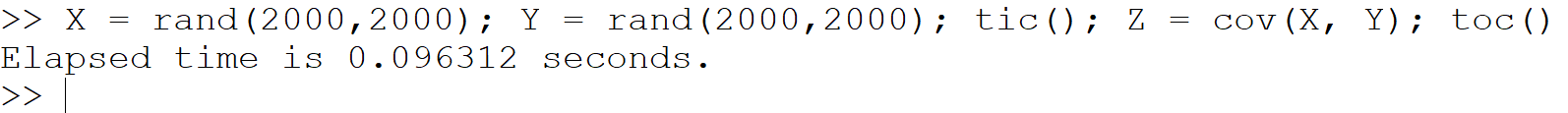
(g) 分散共分散行列:
X = rand(2000,2000); Y = rand(2000,2000); tic(); Z = cov(X, Y); toc()

[image]
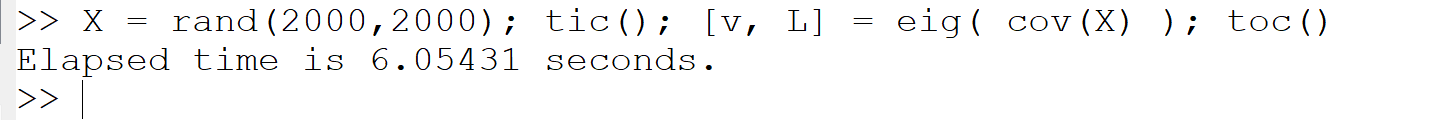
(h) 分散共分散行列の固有値と固有ベクトル（主成分分析）:
X = rand(2000,2000); tic(); [v, L] = eig( cov(X) ); toc()

[image]
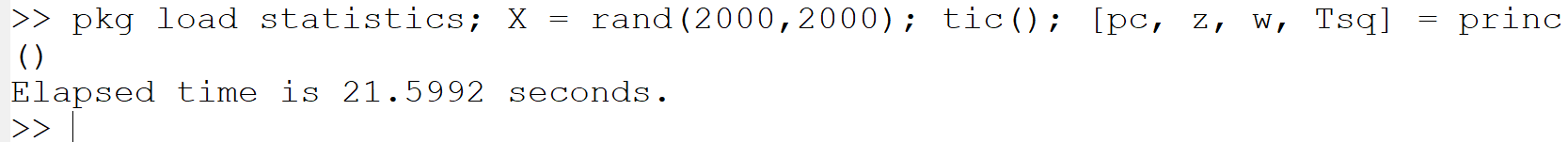
(i) princomp 関数による主成分分析:
pkg load statistics; X = rand(2000,2000); tic(); [pc, z, w, Tsq] = princomp(X); toc()

[image]
(j) 2次元の畳み込み（コンボリューション）:
X = rand(2000,2000); B = rand(21); tic(); Z = conv2(X, B, 'full'); toc()

[image]
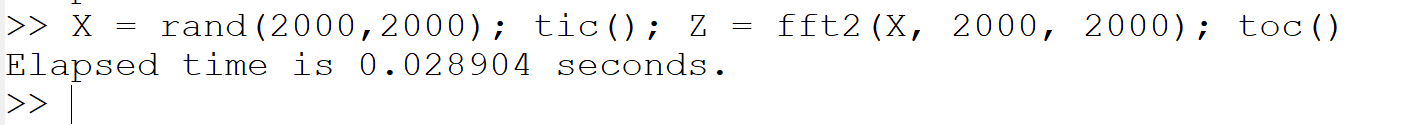
(k) 2次元の高速フーリエ変換 (FFT):
X = rand(2000,2000); tic(); Z = fft2(X, 2000, 2000); toc()

[image]
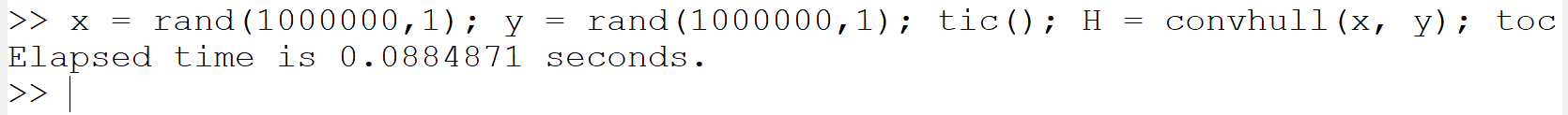
(l) convex hull:
x = rand(1000000,1); y = rand(1000000,1); tic(); H = convhull(x, y); toc()