データの並び x, y を3本の線分で近似
1. エグゼクティブサマリー
本記事では,データの並び x, y を3本の線分で近似するプログラムを扱う。この手法は区分線形関数(piecewise linear function)のフィッティングと呼ばれ,データ点列を3つの区間に分割し,各区間で1次関数による最小二乗近似を行い,残差の総和が最小となる分割位置を探索する。
プログラムは Python で実装されており,NumPy の多項式近似と総当たり探索により最適な2つの端点(区間の境界)を決定する。各線分の傾きと切片,端点座標をコンソールに表示し,散布図上に3本の近似線分を描画する。さらに,残差の分布をヒートマップとして可視化する。
2. 前準備(必要ソフトウェアの入手)
ここでは、最低限の事前準備について説明する。機械学習や深層学習を行う場合は、NVIDIA CUDA、Visual Studio、Cursorなどを追加でインストールすると便利である。これらについては別ページ https://www.kkaneko.jp/cc/dev/aiassist.htmlで詳しく解説しているので、必要に応じて参照してください。
Python 3.12 のインストール(Windows 上) [クリックして展開]
以下のいずれかの方法で Python 3.12 をインストールする。Python がインストール済みの場合、この手順は不要である。
方法1:winget によるインストール
管理者権限のコマンドプロンプトで以下を実行する。管理者権限のコマンドプロンプトを起動するには、Windows キーまたはスタートメニューから「cmd」と入力し、表示された「コマンドプロンプト」を右クリックして「管理者として実行」を選択する。
winget install --scope machine --id Python.Python.3.12 -e --silent --disable-interactivity --force --accept-source-agreements --accept-package-agreements --override "/quiet InstallAllUsers=1 PrependPath=1 Include_pip=1 Include_test=0 Include_launcher=1 InstallLauncherAllUsers=1"--scope machine を指定することで、システム全体(全ユーザー向け)にインストールされる。このオプションの実行には管理者権限が必要である。インストール完了後、コマンドプロンプトを再起動すると PATH が自動的に設定される。
方法2:インストーラーによるインストール
- Python 公式サイト(https://www.python.org/downloads/)にアクセスし、「Download Python 3.x.x」ボタンから Windows 用インストーラーをダウンロードする。
- ダウンロードしたインストーラーを実行する。
- 初期画面の下部に表示される「Add python.exe to PATH」に必ずチェックを入れてから「Customize installation」を選択する。このチェックを入れ忘れると、コマンドプロンプトから
pythonコマンドを実行できない。 - 「Install Python 3.xx for all users」にチェックを入れ、「Install」をクリックする。
インストールの確認
コマンドプロンプトで以下を実行する。
python --versionバージョン番号(例:Python 3.12.x)が表示されればインストール成功である。「'python' は、内部コマンドまたは外部コマンドとして認識されていません。」と表示される場合は、インストールが正常に完了していない。
AIエディタ Windsurf のインストール(Windows 上) [クリックして展開]
Pythonプログラムの編集・実行には、AIエディタの利用を推奨する。ここでは、Windsurfのインストールを説明する。Windsurf がインストール済みの場合、この手順は不要である。
管理者権限のコマンドプロンプトで以下を実行する。管理者権限のコマンドプロンプトを起動するには、Windows キーまたはスタートメニューから「cmd」と入力し、表示された「コマンドプロンプト」を右クリックして「管理者として実行」を選択する。
winget install --scope machine --id Codeium.Windsurf -e --silent --disable-interactivity --force --accept-source-agreements --accept-package-agreements --custom "/SP- /SUPPRESSMSGBOXES /NORESTART /CLOSEAPPLICATIONS /DIR=""C:\Program Files\Windsurf"" /MERGETASKS=!runcode,addtopath,associatewithfiles,!desktopicon"
powershell -Command "$env:Path=[System.Environment]::GetEnvironmentVariable('Path','Machine')+';'+[System.Environment]::GetEnvironmentVariable('Path','User'); windsurf --install-extension MS-CEINTL.vscode-language-pack-ja --force; windsurf --install-extension ms-python.python --force; windsurf --install-extension Codeium.windsurfPyright --force"--scope machine を指定することで、システム全体(全ユーザー向け)にインストールされる。このオプションの実行には管理者権限が必要である。インストール完了後、コマンドプロンプトを再起動すると PATH が自動的に設定される。
【関連する外部ページ】
Windsurf の公式ページ: https://windsurf.com/
必要なライブラリのインストール [クリックして展開]
管理者権限のコマンドプロンプトで以下を実行する。管理者権限のコマンドプロンプトを起動するには、Windows キーまたはスタートメニューから「cmd」と入力し、表示された「コマンドプロンプト」を右クリックして「管理者として実行」を選択する。
pip install -U numpy matplotlib seaborn3. 実行のための準備とその確認手順(Windows 前提)
3.1 プログラムファイルの準備
第5章のソースコードをテキストエディタ(メモ帳,Windsurf 等)に貼り付け,main.py として保存する(文字コード:UTF-8)。
3.2 実行コマンド
コマンドプロンプトでファイルの保存先ディレクトリに移動し,以下を実行する。
python main.py3.3 動作確認チェックリスト
| 確認項目 | 期待される結果 |
|---|---|
| コンソール出力 | 線分1,線分2,線分3 それぞれの傾き,切片,区間が表示される |
| 散布図と近似線分 | データ点が「o」マーカーで表示され,3本の近似線分が色分けされて描画される |
| 端点の注釈 | グラフ上の各区間の端点に座標が注釈として表示される |
| ヒートマップ | 残差の分布がヒートマップとして表示され,最小残差の位置が確認できる |
4. 概要・使い方・実行上の注意
プログラムでは以下のデータを使用する。
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15](float 型)
y = [22, 16, 10, 4, 4, 4, 4, 4, 4, 4, 24, 44, 64, 84, 104]
プログラムはこのデータ配列を3つの連続する区間に分割し,各区間で np.polyfit による1次の最小二乗近似を行う。すべての分割パターンについて残差の総和を計算し,残差が最小となる2つの端点(インデックス i, j)を総当たり探索で決定する。
最適な端点が決まると,各線分の傾き・切片・区間をコンソールに表示し,散布図上にデータ点と3本の近似線分を描画する。各区間の端点には座標の注釈が付与される。
さらに,すべての (i, j) の組み合わせに対する残差をヒートマップとして可視化する。探索対象外のセル(無効な組み合わせ)は NaN として処理され,seaborn により自動的に除外される。
ソースコードは第5章に掲載する。
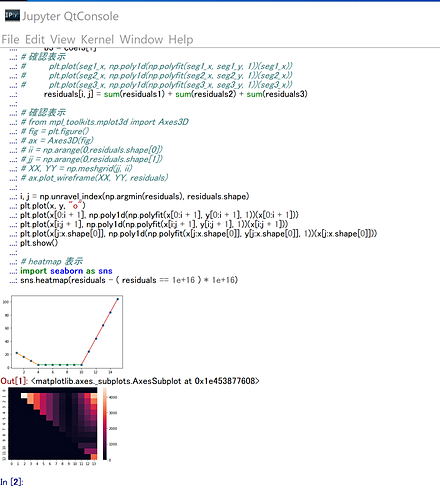
5. ソースコード
3本の線分で x, y データを近似するプログラムのソースコードを以下に示す。
# 3本の線分で x, y を近似
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15], dtype=float)
y = np.array([22, 16, 10, 4, 4, 4, 4, 4, 4, 4, 24, 44, 64, 84, 104])
n = x.shape[0]
residuals = np.full((n - 2, n - 1), np.inf)
for i in range(1, n - 2):
coef1, res1, *_ = np.polyfit(x[:i+1], y[:i+1], 1, full=True)
for j in range(i + 1, n - 1):
_, res2, *_ = np.polyfit(x[i:j+1], y[i:j+1], 1, full=True)
_, res3, *_ = np.polyfit(x[j:], y[j:], 1, full=True)
residuals[i, j] = sum(res1) + sum(res2) + sum(res3)
i, j = np.unravel_index(np.argmin(residuals), residuals.shape)
# 最適な3区間の係数を求める
c1 = np.polyfit(x[:i+1], y[:i+1], 1)
c2 = np.polyfit(x[i:j+1], y[i:j+1], 1)
c3 = np.polyfit(x[j:], y[j:], 1)
# 各線分の傾きと切片,端点座標を表示
print(f"線分1: 傾き={c1[0]:.2f}, 切片={c1[1]:.2f} 区間 x=[{x[0]:.0f}, {x[i]:.0f}]")
print(f"線分2: 傾き={c2[0]:.2f}, 切片={c2[1]:.2f} 区間 x=[{x[i]:.0f}, {x[j]:.0f}]")
print(f"線分3: 傾き={c3[0]:.2f}, 切片={c3[1]:.2f} 区間 x=[{x[j]:.0f}, {x[n-1]:.0f}]")
# 散布図と近似線分の描画
plt.plot(x, y, "o", label="data")
plt.plot(x[:i+1], np.poly1d(c1)(x[:i+1]), label="seg 1")
plt.plot(x[i:j+1], np.poly1d(c2)(x[i:j+1]), label="seg 2")
plt.plot(x[j:], np.poly1d(c3)(x[j:]), label="seg 3")
# 端点の座標を注釈として表示
for idx in [0, i, j, n - 1]:
yv = np.poly1d(c1 if idx <= i else c2 if idx <= j else c3)(x[idx])
plt.annotate(f"({x[idx]:.0f}, {yv:.1f})", (x[idx], yv), textcoords="offset points", xytext=(0, 10), ha="center", fontsize=8)
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
plt.show()
# ヒートマップ表示(無効値を NaN に置換)
heatmap_data = residuals.copy().astype(float)
heatmap_data[heatmap_data == np.inf] = np.nan
sns.heatmap(heatmap_data)
plt.xlabel("j")
plt.ylabel("i")
plt.show()
6. まとめ
区分線形近似
データの並び x, y を3本の線分で近似する手法である。データ配列を3つの区間に分割し,各区間で1次関数による最小二乗近似を行う。
端点の総当たり探索
区間の境界となる2つの端点(インデックス i, j)の全組み合わせについて残差の総和を計算し,残差が最小となる分割位置を決定する。
近似係数の算出と表示
np.polyfit により各区間の近似直線の傾きと切片を求め,コンソールに表示する。
散布図による可視化
データ点と3本の近似線分を散布図上に描画し,各端点に座標の注釈を付与する。
ヒートマップによる残差分布の可視化
全 (i, j) の組み合わせに対する残差をヒートマップで表示し,最適な分割位置の近傍における残差の変化を確認できる。
![[kaneko lab.]](https://www.kkaneko.jp/info/logo_png.png)