R システムの機能一覧

【概要】

R システムは統計解析とデータ操作に特化したシステムであり，以下の特徴的な機能を持つ．

ベクトル演算が基本であり，データを効率的に処理できる．リサイクル規則により，長さの異なるベクトル間の演算も可能である．
データフレームという2次元データ構造を提供し，異なるデータ型の列を持つテーブルデータを扱える．subset()やmerge()などの関数で柔軟なデータ操作が可能である．
統計解析に特化した豊富な関数群があり，回帰分析，検定，多変量解析などを簡単に実行できる．特にlm()やglm()による回帰分析，t.test()による検定など，機能が充実している．
ggplot2などの拡張パッケージを用いることで，高度なデータ可視化も実現できる．また，tidyverseパッケージ群によって，より直感的なデータ操作が可能である．

Rシステムについて

データシステム演習（R システム，Shiny を使用）: 別ページ »にまとめ
データサイエンス演習（R システムを使用）: 別ページで説明している．

Rシステムのインストール

Windows での R システムのインストール: 別ページ »で説明
Ubuntu での R システムのインストール: 別ページ »で説明

【目次】

R システムのインストール手順（Windows上）
関数
パッケージ
データの読み込み
データ型
オブジェクトの一覧，データ型の取得，オブジェクトの構造の取得
論理演算，比較演算，数値演算，文字列に関する演算など
ベクトルに関する演算子と関数
行列に関する演算子と関数
リストに関する演算子と関数
データフレームに関する演算子と関数
条件分岐と繰り返し
グラフの概要
統計解析関連の機能
データ操作関連の機能
プログラミング関連の機能

【関連する外部ページ】

R システムの CRAN の URL: https://cran.r-project.org/

【サイト内の関連情報】

種々のまとめページ: [人工知能，データサイエンス，データベース，３次元]， [Windows]， [Ubuntu]， [Python （Google Colaboratory を含む）]， [C/C++言語プログラミング用語説明]， [R システムの機能]， [Octave]

R システムのインストール手順（Windows上）

【要点】

R システムは基本システムと統合開発環境（RStudio）の2段階でインストールする．インストールには管理者権限が必要である．

R システムのインストール：
1. 公式サイト CRAN（The Comprehensive R Archive Network）にアクセスする．
2. 「Download R for Windows」→「base」の順にクリックする．
3. 最新版の R インストーラー（R-x.x.x-win64.exe）をダウンロードする．
4. ダウンロードしたインストーラーを右クリックし，「管理者として実行」を選択する．
5. インストール言語を選択する．
6. 情報ページの内容を確認し，「次へ」をクリックする．
7. インストール先フォルダを指定する（デフォルト：C:\Program Files\R\R-x.x.x）．
8. コンポーネントの選択では，デフォルト設定のまま「次へ」をクリックする．
9. スタートメニューフォルダの設定を確認し，「次へ」をクリックする．
10. 追加タスクの設定（デスクトップアイコンの作成など）を行い，「次へ」をクリックする．
RStudio のインストール：
1. 公式サイト Posit Download にアクセスする．
2. 「RStudio Desktop」セクションから，Windows用インストーラー（RStudio-x.x.x.exe）をダウンロードする．
3. ダウンロードしたインストーラーを右クリックし，「管理者として実行」を選択する．
4. 「Next」をクリックしてインストールを開始する．
5. ライセンス条項を確認し，「I accept the agreement」を選択して「Next」をクリックする．
6. インストール先を指定する（デフォルト：C:\Program Files\RStudio）．
7. 「Install」をクリックしてインストールを実行する．
8. インストール完了後，「Finish」をクリックする．
初期動作確認：
1. デスクトップ上の RStudio アイコンをダブルクリックする．
2. RStudio が起動し，R コンソールが表示されることを確認する．
3. コンソールで以下のコマンドを実行して，バージョン確認，基本的な計算，グラフ描画の確認を行う．
```
version
1 + 2
plot(1:10, type="l")
```
主な設定：
1. RStudio の表示言語設定：Tools → Global Options → General → Language
2. 作業ディレクトリの設定：Session → Set Working Directory → Choose Directory
3. 基本的な統計解析パッケージのインストール
  例：tidyverse, ggplot2, dplyr のインストール
```
install.packages(c("tidyverse", "ggplot2", "dplyr"))
```

関数

help(＜関数名＞): 関数の概要を表示する
example(＜関数名＞): 関数の使用例を表示する
関数名: 関数のソースコードを表示する

関数のヘルプを検索する場合は「help.search()」関数を使用する

パッケージ

chooseCRANmirror(): CRAN（総合Rアーカイブネットワーク）ミラーサイトを選択する
utils:::menuInstallPkgs(): パッケージをインストールする
install.packages(＜パッケージ名＞): 指定したパッケージをインストールする
library(): インストール済みのパッケージ一覧を表示する
update.packages(): インストール済みのパッケージを更新する
library(＜パッケージ名＞): 指定したパッケージを読み込む
library(help="＜パッケージ名＞"): 指定したパッケージの概要を表示する
example(＜パッケージ名＞): 読み込み済みパッケージの使用例を表示する
help(＜関数名＞): 読み込み済みパッケージのヘルプを表示する

データの読み込み

data(): データの一覧を表示する
data(package="＜パッケージ名＞"): 指定したパッケージ内のデータ一覧を表示する
data(＜データ名＞): 指定したデータを読み込む
- data(iris): Iris（アヤメの花の測定データ）データセットを読み込む
```
data(iris)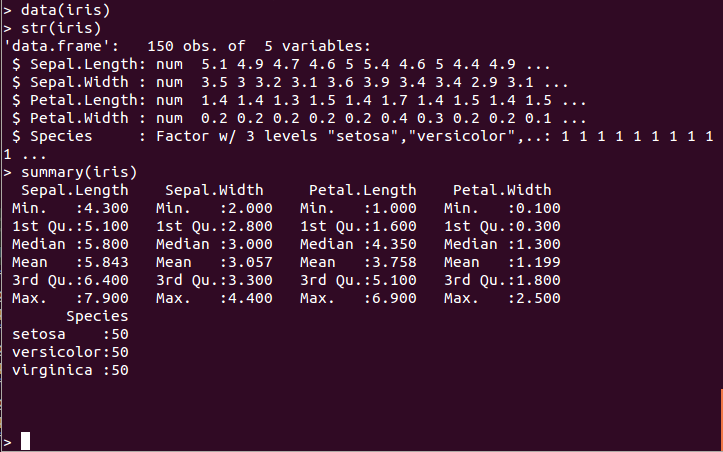
```
- data(lung): lung（肺がん患者の生存データ）データセットを読み込む
```
data(lung)
```
?(＜データ名＞)またはhelp(＜データ名＞): 読み込まれたデータの概要を表示する
```
data(iris)
?(iris)
```
example(＜データ名＞): 読み込まれたデータの使用例を表示する

データ型

主要なデータ型は以下のとおりである．

TRUE，FALSE: 論理型（logical）オブジェクト
NA: Not Available（欠損値）
NULL: 空ベクトルなどを表す特殊な値
NaN: Not a Number（非数値）
Inf，-Inf: Infinitive（正の無限大），負の無限大
数値型（numeric）: 整数または倍精度浮動小数点数
複素数型（complex）
文字列型（character）: ダブルクオーテーションで囲んで表す（例: "apple"）
日時型
ベクトル型（vector）
行列型（matrix）
配列型（array）
リスト型（list）
データフレーム型（data frame）
因子型（factor）
順序付き因子型
テーブル型（table）

ベクトルの生成

【要点】

ベクトルは同じデータ型の要素を並べたものである．変数 t に要素 2，1，3 のベクトルを格納する場合は，次のように記述する．

t <- c(2, 1, 3)

ベクトルは数値以外の要素も格納できるが，すべての要素が同じデータ型である必要がある．

ベクトルは c() 関数で生成する
- 例1: c(1,2,3) - 要素 1，2，3 のベクトル
- 例2: c(1:3) - 要素 1，2，3 のベクトル（コロンで区切った先頭と末端の間を公差1で生成）
- 例3: c(3:1) - 要素 3，2，1 のベクトル（コロンで区切った先頭と末端の間を公差-1で生成）
numeric(＜要素数＞): すべての要素が0のベクトルを生成する
seq(): 等差数列のベクトルを生成する
例1: seq(2, 10, by = 1.5) - 初項2，公差1.5で10以下の数列を生成
例2: seq(2, 5, along = runif(8)) - 初項2，終項5で長さ8の等差数列を生成
例3: seq(length=10, from=2, by=1) - 初項2，公差1で長さ10の等差数列を生成
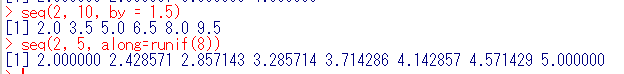
rep(): 要素を繰り返してベクトルを生成する
例: rep(3, 5) - 要素3を5回繰り返したベクトルを生成
runif(): 一様分布の乱数ベクトルを生成する
例: runif(10) - 区間(0,1)の一様分布から長さ10の乱数ベクトルを生成
rnorm(): 正規分布の乱数ベクトルを生成する
例: rnorm(10) - 標準正規分布（平均0，分散1）から長さ10の乱数ベクトルを生成
rpois(): ポアソン分布の乱数ベクトルを生成する
as.vector(): 因子などのオブジェクトをベクトルに変換する
```
V <- as.vector(L)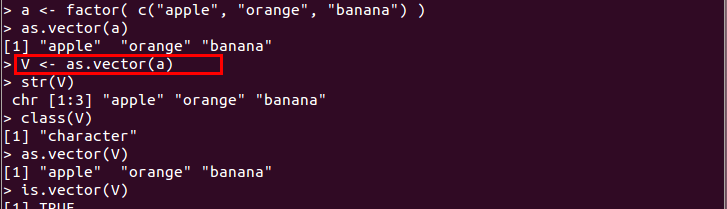
```

行列の生成

【要点】

変数 m に2行3列の行列を格納する場合の例を示す．

1 3 5
2 4 6

次のように記述する．nrowは行数，ncolは列数を指定する．

m <- matrix( c(1, 2, 3, 4, 5, 6), nrow = 2, ncol = 3 )

行列は数値以外の要素も格納できるが，すべての要素が同じデータ型である必要がある．

matrix(): ベクトルから行列を生成する
matrix()関数では，要素のベクトル，行数，列数を指定する．ベクトルの要素は列方向に順に格納される．
```
m <- matrix( c(1, 2, 3, 4), nrow = 2, ncol = 2 )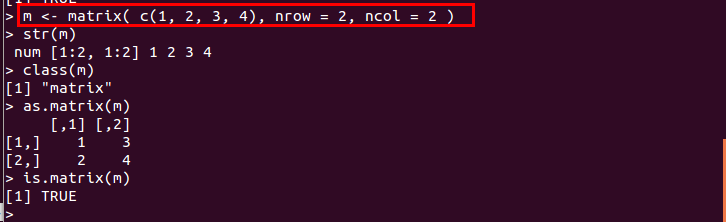
```
引数名「nrow=」，「ncol=」は省略可能である．
```
m2 <- matrix( c(1, 2, 3, 4), 2, 2 )
```
引数「byrow=TRUE」を指定すると，要素が行方向に格納される．
```
m <- matrix( c(1, 2, 3, 4), byrow=TRUE, nrow = 2, ncol = 2 )
```
matrix(0, nrow=＜行数＞, ncol=＜列数＞) : 要素がすべて 0 の行列を生成する
rnorm()関数は，正規分布（ガウス分布）に従う乱数を生成してベクトルを作成する関数である．これをmatrix()関数と組み合わせて使用することができる．
diag() : 対角行列を生成する

対角行列の例
rbind() : 複数のベクトル等を縦方向に結合して行列を生成する
cbind() : 複数のベクトル等を横方向に結合して行列を生成する

rbind と cbind の例
as.matrix() : データフレームなどのオブジェクトを行列に変換する
この関数は，データフレームの内容を行列として扱いたい場合に使用する．例えば，データフレームに対して行列の演算を適用したい場合には，この関数で行列に変換する必要がある．
```
m <- as.matrix(d)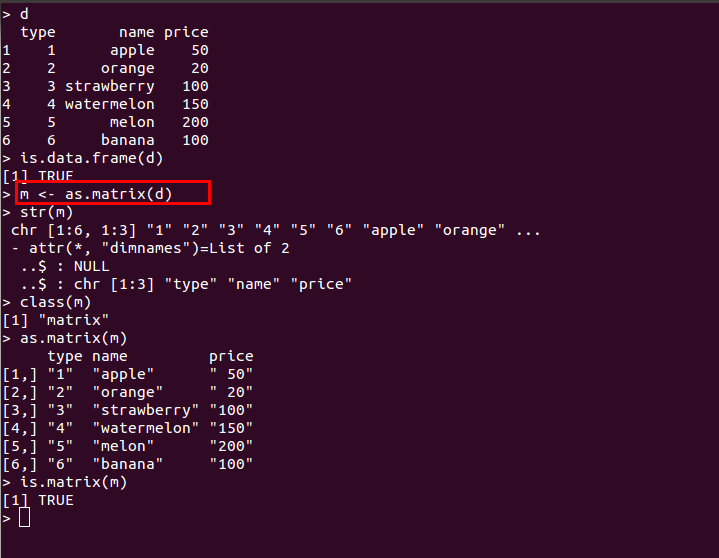
```
data.matrix() : データフレームなどのオブジェクトを行列に変換する
data.matrix()関数の特徴として，文字列データは自動的に数値に変換される（下の実行例を参照）．
```
m <- data.matrix(d)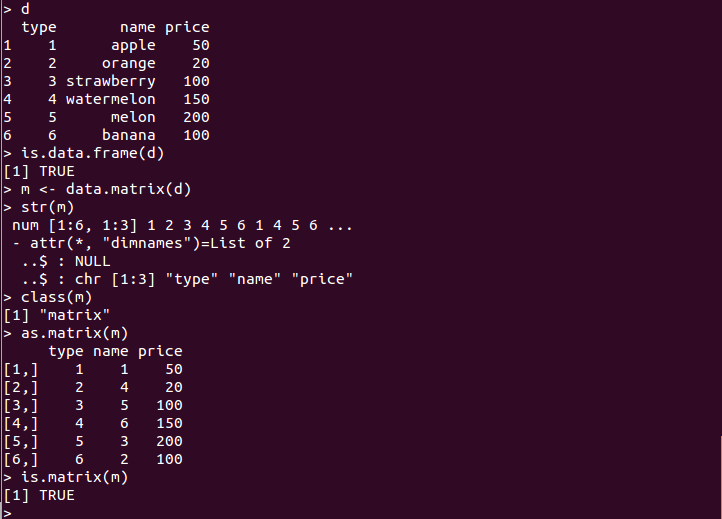
```

リストの生成

【要点】

変数 L にリストを作成して格納する場合，"apple"，5，"fruits"という要素を持つリストは次のように記述する．

L <- list("apple", 5, "fruits")

リストを生成するにはlist()関数を使用する
```
L <- list("apple", 5, "fruits")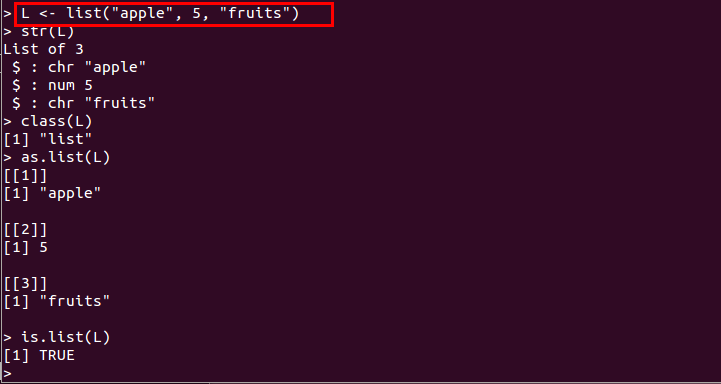
```

データフレームの生成

【要点】

データフレームは，「同じ長さのベクトルを要素として持つリスト構造」として実装されている．例えば，以下のような属性を持つデータフレームを作成する場合：

type属性: 1，2，3，4，5，6
name属性: "apple"，"orange"，"strawberry"，"watermelon"，"melon"，"banana"
price属性: 50，20，100，150，200，100

次のように記述する：

d <- data.frame( type = c(1:6),
name = c("apple", "orange", "strawberry", "watermelon", "melon", "banana"),
price = c(50, 20, 100, 150, 200, 100) )

データフレームを生成するには，属性名とベクトルの組み合わせを指定してdata.frame()関数を使用する

d <- data.frame( type = c(1:6),
name = c("apple", "orange", "strawberry", "watermelon", "melon", "banana"),
price = c(50, 20, 100, 150, 200, 100) )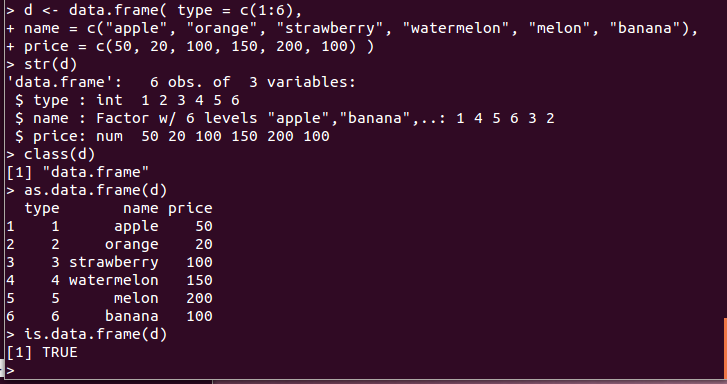

as.data.frame() : 行列などのオブジェクトをデータフレームに変換する
```
d <- as.data.frame(m)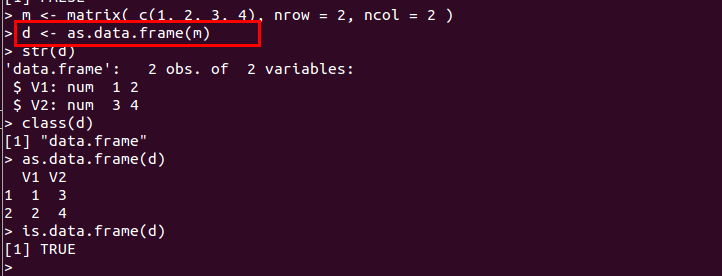
```

因子の生成，因子に関するデータ型の変換

因子を生成するにはfactor()関数を使用する
```
a <- factor( c("apple", "orange", "banana") )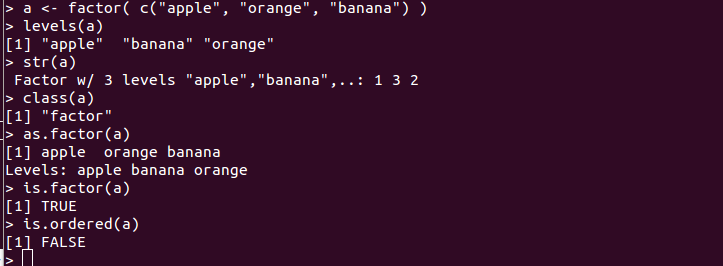
```
as.numeric() : カテゴリ変数を数値に変換する
例１
各因子に対して固有の整数値（通し番号）が割り当てられる
```
L <- as.factor( c("1.2", "2.4", "2.1", "1.2") )
as.numeric(L)
```
例２
同様に，各因子に固有の整数値（通し番号）が割り当てられる．Speciesは "setosa"，"versicolor"，"virginica"の3つの値を取り得るが，as.numericの結果として1，2，3が得られる．
```
data(iris)
attach(iris)
class(iris)
summary(iris)
as.numeric (Species)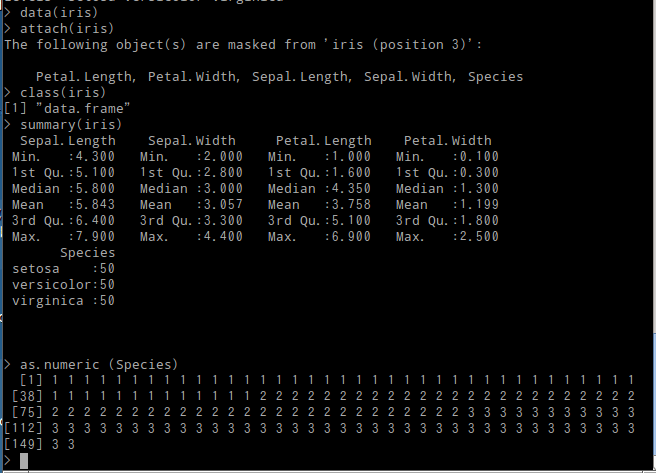
```
例３
as.character関数と組み合わせることで，因子を一旦文字列に変換した後に数値へ変換することができる．
```
L <- as.factor( c("1.2", "2.4", "2.1", "1.2") )
as.numeric( as.character(L) )
```

順序付き因子の生成

順序付き因子を生成するにはordered()関数を使用する
```
b <- ordered( c("apple", "orange", "banana") )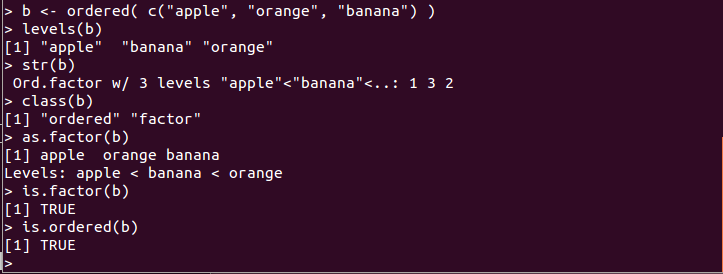
```

テーブルの生成

table(V) : ベクトルVから度数分布を表すテーブルを生成する
生成されたテーブルは，各因子の値に対する出現頻度（度数分布）を表示する
```
t <- table( c(1, 3, 2, 1, 4, 5, 4, 4, 2, 4) )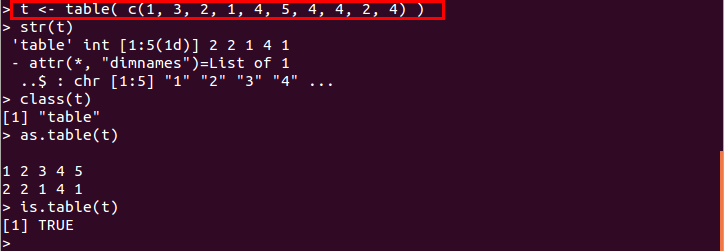
```

table(V1, V2) : 2つのベクトルV1，V2から，クロス集計表（分割表）を生成する

data(warpbreaks)
table(warpbreaks$wool)
table(warpbreaks$tension)
table(warpbreaks$wool, warpbreaks$tension)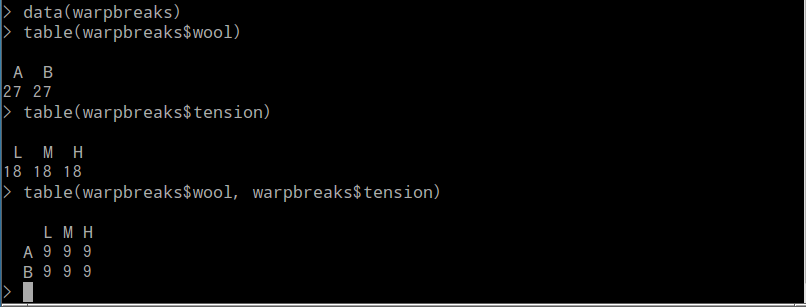

数値データを区間に分割して頻度を集計するには，cut()関数とtable()関数を組み合わせて使用する
```
t <- table( cut( c(3, 15, 2, 8, 22, 18, 4), breaks=c(0, 10, 20, 30) ) )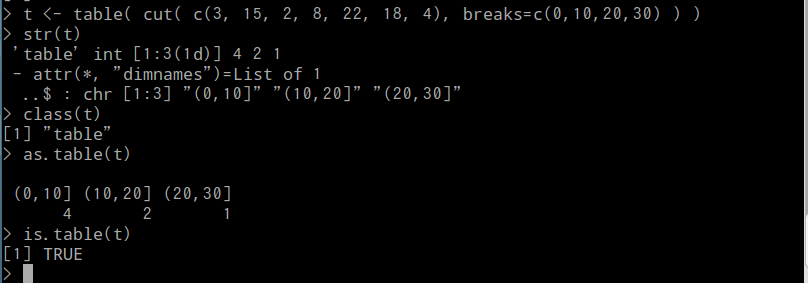
```
二元分割表（two-way contingency table）を作成する例：
```
data(warpbreaks)
table( cut( warpbreaks$breaks, c(0, 10, 20, 30, 40, 50, 60, 70) ), warpbreaks$wool )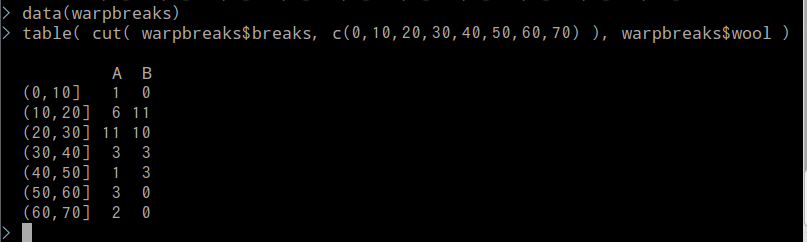
```

論理条件に基づくクロス集計表も作成可能である

data(warpbreaks)
table( warpbreaks$wool, warpbreaks$tension == "L" )

トランザクションの生成

データマイニングにおけるアイテム集合や規則に関するトランザクションデータ

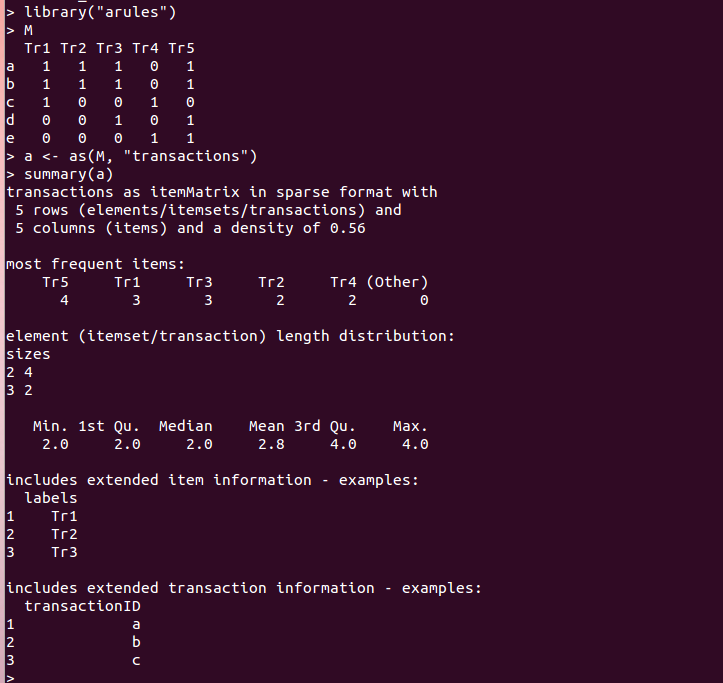
文字列の生成

RGB３原色の色を文字列として表現する方法がある．白色は"#FFFFFF"，黒色は"#000000"のように表現する．

grey()：数値のベクトル → 色のベクトル（文字列表記されたRGB３原色の色）
灰色の生成を行う
rgb()：数値のベクトル数値のベクトル数値のベクトル ... → 色のベクトル（文字列表記されたRGB３原色の色）
引数は，red，green，blue，alpha（透明度），maxColorValue，namesである．ただし，red，green，blue以外は省略可能である．

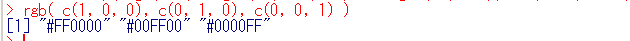
オブジェクトの一覧，データ型の取得，オブジェクトの構造の取得

objects()：オブジェクトの一覧を表示
```
objects()
```
class()，typeof()：データ型の取得
データ型を取得するには，typeof()関数やclass()関数を使用する．ベクトルの場合，要素の型が表示される（ベクトルは同じ型のデータの並びという規則があるため，問題は生じない）．
```
d <- data.frame( type = c(1:6),
name = c("apple", "orange", "strawberry", "watermelon", "melon", "banana"),
price = c(50, 20, 100, 150, 200, 100) )
typeof(d)
class(d)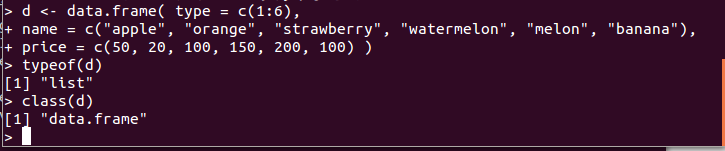
```
```
m <- matrix( c(1, 2, 3, 4, 5, 6), nrow=2, ncol=3 )
typeof(m)
class(m)
```
その他の例

str()：オブジェクトの構造を取得

d <- data.frame( type = c(1:6),
name = c("apple", "orange", "strawberry", "watermelon", "melon", "banana"),
price = c(50, 20, 100, 150, 200, 100) )
str(d)

m <- matrix( c(1, 2, 3, 4, 5, 6), nrow=2, ncol=3 )
str(m)

論理演算，比較演算，数値演算，文字列に関する演算など

論理和，論理積，否定

【評価結果が論理オブジェクト】

||：論理オブジェクトのベクトル論理オブジェクトのベクトル → 論理オブジェクト
論理和の演算（引数がベクトルの場合，先頭要素のみを使用した論理和）
&&：論理オブジェクトのベクトル論理オブジェクトのベクトル → 論理オブジェクト
論理積の演算（引数がベクトルの場合，先頭要素のみを使用した論理積）

【評価結果が論理オブジェクトのベクトル】

|：論理オブジェクトのベクトル論理オブジェクトのベクトル → 論理オブジェクトのベクトル
ベクトル化論理和の演算
&：論理オブジェクトのベクトル論理オブジェクトのベクトル → 論理オブジェクトのベクトル
ベクトル化論理積の演算
!：論理オブジェクトのベクトル → 論理オブジェクトのベクトル
否定の演算

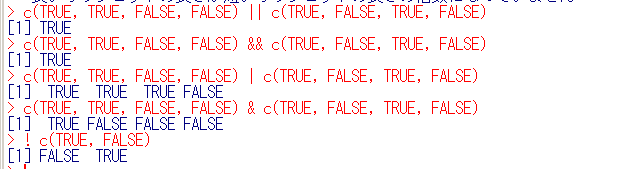
論理和，論理積，否定の例

比較

【評価結果が論理オブジェクト】

all.equal：比較可能なオブジェクトのベクトル比較可能なオブジェクトのベクトル → 論理オブジェクト
ほぼ等しいかの判定（引数がベクトルの場合，先頭要素のみの比較）

all.equalの使用例

all.equalでは，引数がベクトルの場合，先頭要素のみを比較

【評価結果が論理オブジェクトのベクトル】

==：比較可能なオブジェクトのベクトル比較可能なオブジェクトのベクトル → 論理オブジェクトのベクトル
等しいかの比較
!=：比較可能なオブジェクトのベクトル比較可能なオブジェクトのベクトル → 論理オブジェクトのベクトル
等しくないかの比較
>：比較可能なオブジェクトのベクトル比較可能なオブジェクトのベクトル → 論理オブジェクトのベクトル
より大きいかの比較
>=：比較可能なオブジェクトのベクトル比較可能なオブジェクトのベクトル → 論理オブジェクトのベクトル
以上かの比較
<：比較可能なオブジェクトのベクトル比較可能なオブジェクトのベクトル → 論理オブジェクトのベクトル
より小さいかの比較
<=：比較可能なオブジェクトのベクトル比較可能なオブジェクトのベクトル → 論理オブジェクトのベクトル
以下かの比較

論理オブジェクトを返す主要な演算子の例

数値に関する二項演算子

+：数値のベクトル数値のベクトル → 数値のベクトル
加算演算
-：数値のベクトル数値のベクトル → 数値のベクトル
減算演算
*：数値のベクトル数値のベクトル → 数値のベクトル
乗算演算
/：数値のベクトル数値のベクトル → 数値のベクトル
除算演算
^：数値のベクトル数値のベクトル → 数値のベクトル
べき乗演算
^の代わりに**も使用可能である．
%/%：数値のベクトル数値のベクトル → 数値のベクトル
整数除算演算
%%：数値のベクトル数値のベクトル → 数値のベクトル
剰余演算（除算の余りを求める）

数値に関する二項演算子をベクトルに適用した例

長さが異なるベクトルが引数として与えられた場合，長さの短いベクトルが繰り返し使用される（「リサイクル規則」）

数値に関する単項演算子

sqrt()：数値のベクトル → 数値のベクトル
平方根の計算

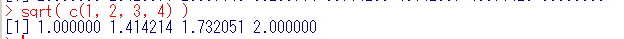
単項演算子はベクトルの各要素に適用される
abs()：数値のベクトル → 数値のベクトル
絶対値の計算
sign()：数値のベクトル → 数値のベクトル
符号の判定
round()，floor()，ceiling()：数値のベクトル → 数値のベクトル
それぞれ，四捨五入，切り捨て（x以下の最大の整数），切り上げ（x以上の最小の整数）を計算
log()，log10()，log2()：数値のベクトル → 数値のベクトル
それぞれ，自然対数（底がe），常用対数（底が10），2を底とする対数を計算
exp()：数値のベクトル → 数値のベクトル
指数関数の計算
sin()，cos()，tan()，asin()，acos()，atan()：数値のベクトル → 数値のベクトル
三角関数とその逆関数の計算

文字列に関する演算子と関数

nchar()：文字列の長さを取得する
paste()：文字列を連結する
```
paste( "hoge2", "hoge3", "hoge4" )
```

ベクトルに関する演算子と関数

ベクトルを引数にとる演算子に関する規則

「『X』のベクトルを引数にとる演算子」は，「X」型の単一の値も引数として受け付ける．

「+」は，ベクトルを引数にとる演算子であり，数値1個も引数として受け付ける．
2個以上の引数をとる演算子に長さが異なるベクトルが引数として与えられた場合，長さの短いベクトルが繰り返し使用される（これを「リサイクル規則」という）．
* ただし，長いベクトルの長さは，短いベクトルの長さの整数倍である必要がある．

リサイクル規則の例．長さが整数倍でない場合は実行時エラーとなる．

添え字に関する操作

[] で，添え字として整数を1つ指定する場合

添え字として整数を1つ指定する場合
[] で，添え字として整数のベクトルを指定する場合
整数のベクトルを指定すると，指定された整数値を添え字として扱い，ベクトル内の整数値の順番に従って要素が取り出され，新しいベクトルが生成される．

整数のベクトルを指定する場合
[] で，添え字として-c(数値の並び)を指定する場合
「-c(整数のベクトル)」は，整数のベクトル c(...) の前にマイナス記号「-」を付けたものである．この表記を用いると，指定された添え字以外の要素を，元のベクトルの順序を保持したまま取り出すことができる．例えば，次のように記述する．
```
x[-c(1,2)]
```
[] で，添え字としてTRUE，FALSE のベクトルを与えると，TRUE となっている位置の要素のみが取り出され，新しいベクトルが生成される．
[] で，添え字として条件式を指定する場合
条件式を満たす要素のみから構成されるベクトルが得られる．

ベクトルから要素をランダムに抽出する関数 sample

X = c(1, 3, 4, 6, 2, 7, 5)
X
sample(X, 3, replace=FALSE)
sample(X, 3, replace=FALSE)
sample(X, 3, replace=FALSE)

条件に合致する要素の添え字を取得する関数 which

ベクトルの集約と統計量

length(V)：ベクトル V の長さ（要素数）を返す
max(V)，min(V)：ベクトル V の最大値，最小値を返す
range(V)：ベクトル V の最大値と最小値をベクトルとして返す
sum(V)：ベクトル V の要素の総和を計算する
例
```
sum( c(1, 2, 3) )
```
mean(V)：ベクトル V の要素の算術平均を計算する
prod(V)：ベクトル V の要素の積を計算する
cor(X,Y)：ベクトル X，Y の相関係数を計算する
var(V)：ベクトル V の不偏分散を計算する
var(X, Y)：ベクトル X，Y の不偏共分散を計算する
sd(V)：ベクトル V の要素の不偏標準偏差を計算する
summary(V)：ベクトル V の基本統計量の要約を表示する

ベクトルに関する関数

c：複数のベクトルを連結する
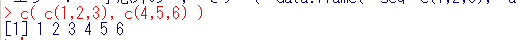
append：ベクトルに要素を挿入する引数「after=...」を指定すると，after番目の要素の直後に挿入される．
cut(V，＜区間を示すベクトル＞)：区間ごとの要素数を数える
出力はベクトルとなり，各要素は区間を表す因子となる
```
V <- rnorm(20, 5)
cut( V, c(0:10) )
```
要素の出現回数を数える table 関数
sort(V)：ベクトル V の要素を昇順または降順に並び替える
unique(V)：ベクトル V から重複要素を除去する
重複する要素を1つだけ残して除去する
```
X = c(2, 1, 1, 3, 5, 2, 4, 4)
unique(X)
```
duplicated(V)：ベクトル V の要素の重複を確認する
重複要素がある位置に TRUE を返す
```
X = c(2, 1, 1, 3, 5, 2, 4, 4)
duplicated(X)
```
table(V)：ベクトル V の各要素の出現回数を集計する
各要素の出現回数を表示する
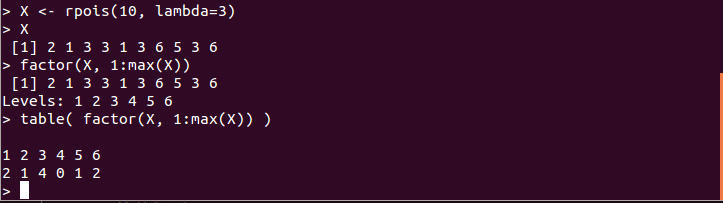
rle(V)：ベクトル V の連続する同一要素の長さ（ランレングス）を計算する
```
X = c(2, 1, 1, 3, 5, 2, 4, 4)
rle(X)
```
sapply(V, f)：ベクトル V の各要素に関数 f を適用し，結果を新しいベクトルとして返す
```
V <- c(1, 2, 3)
sapply(V, function(x) (x * 2))
```

行列に関する演算子と関数

添え字に関する操作

[]：行列の要素にアクセスする添字演算子
x[i,j] は i 行 j 列の要素を指定する． x[i,] は i 行のすべての要素を指定する． x[,j] は j 列のすべての要素を指定する． x[,c(j,k)] は j 列と k 列を取り出して新しい2列の行列を生成する．
order()：要素の順序を取得し，並び替えを行う
- order(m[i,])：i行の要素の順序を取得
- order(m[,j])：j列の要素の順序を取得
- m[order(m[i,]),]：i行の値に基づいて行を並び替え
- m[,order(m[,j])]：j列の値に基づいて列を並び替え

行列に関する操作

summary(m)：行列 m の統計量の要約
数値要約として，最小値，第一四分位点，中央値（median），平均値，第三四分位点，最大値が表示される．
```
m <- matrix( c(1, 2, 3, 4, 5, 6), nrow=2, ncol=3 )
summary(m)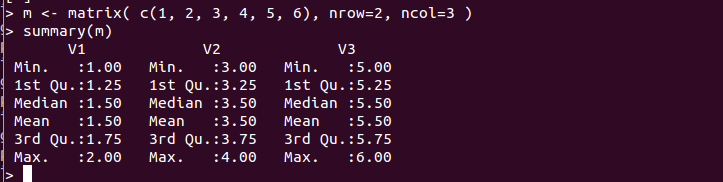
```
diag(m)：行列 m の対角要素の取得
t(m)：行列 m の転置行列
m1 %*% m2：行列 m1，m2 の行列積
「*」は行列にも使用できるが，その場合は要素同士の単純な掛け算となる． %*%は，行列同士の行列積，または行列とベクトルの積を計算する（このとき，ベクトルは幅あるいは高さ1の行列として扱われる）．
```
X <- matrix( runif(2000 * 2000), 2000, 2000 )
Y <- matrix( runif(2000 * 2000), 2000, 2000 )
Z = X %*% Y
```
crossprod()：転置して行列積を計算
「crossprod(c(2:4), c(1:3))」は「t(c(2:4)) %*% c(1:3)」と同等である．
lu(m)：行列 m のLU分解（LU decomposition）
lu() 関数は Matrix パッケージが提供する関数であり，通常の行列オブジェクトではなく Matrix クラスのオブジェクトに適用する必要がある．
```
install.packages("Matrix")
library("Matrix")
X <- matrix( runif(2000 * 2000), 2000, 2000 )
Z = lu( Matrix(X) )
```
solve(m)：正方行列 m の逆行列を求める，または線形連立方程式の解を計算
```
X <- matrix( runif(2000 * 2000), 2000, 2000 )
Z = solve( X )
```
library(MASS); ginv(m)：行列 m のムーア・ペンローズ型一般逆行列を計算
det(m)：正方行列 m の行列式（determinant）の値を計算
```
X <- matrix( runif(2000 * 2000), 2000, 2000 )
Z = det( X )
```
eigen(m)：行列 m の固有値と固有ベクトルを計算
svd(m)：特異値分解（Singular Value Decomposition; SVD）を実行，m = U%*%S%*%V
```
X <- matrix( runif(2000 * 2000), 2000, 2000 )
Z = svd( X )
```
qr(m)：QR分解（QR factorization，QR decomposition）を実行
```
X <- matrix( runif(2000 * 2000), 2000, 2000 )
Z = qr( X )
```

cov(m)：分散共分散行列を計算

X <- matrix( runif(2000 * 2000), 2000, 2000 )
Z = cov( X )

分散共分散行列の固有値と固有ベクトルを計算（主成分分析）

X <- matrix( runif(2000 * 2000), 2000, 2000 )
Z = eigen( cov( X ) )

chol(m)：正定値対称行列のコレスキー分解（Cholesky分解）を実行
cor(m)：相関行列を計算
fft(m)：2次元の高速フーリエ変換（FFT）を実行．fft()はRの標準機能（base）に含まれる関数であり，追加のパッケージは不要である．
```
X <- matrix( runif(2000 * 2000), 2000, 2000 )
Z = fft( X )
```

library(relimp); showData(m)：行列 m を別ウィンドウで表示

library(relimp)
m <- matrix( c(1, 2, 3, 4), nrow = 2, ncol = 2 )
showData(m)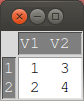

apply(m，c(1,2)，f)：行列 m の全要素に関数 f を適用し，結果として新しい行列を生成
```
m <- matrix( c(1, 2, 3, 4, 5, 6), nrow = 2, ncol = 3 )
apply(m, c(1, 2), function(x) (x * 2))
```
apply(m，＜次元の指定＞，f)：行列 m の行ベクトルまたは列ベクトルごとに関数 f を適用し，結果を返す
＜次元の指定＞は以下の通り：
- 1：行方向の処理
- 2：列方向の処理
```
m <- matrix( c(1, 2, 3, 4, 5, 6), nrow = 2, ncol = 3 )
apply(m, 1, max)
apply(m, 2, max)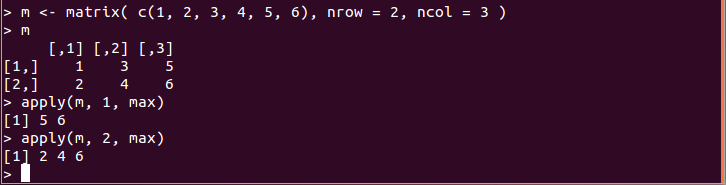
```
以下のように，各要素を2倍にする関数などを適用することも可能である．
```
m <- matrix( c(1, 2, 3, 4, 5, 6), nrow = 2, ncol = 3 )
apply(m, 1, function(x) (x * 2))
apply(m, 2, function(x) (x * 2))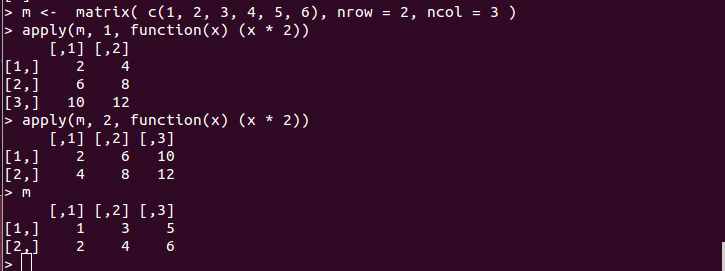
```

edit(m)：行列 m を対話的に編集

m <- matrix( c(1, 2, 3, 4), nrow = 2, ncol = 2 )
edit(m)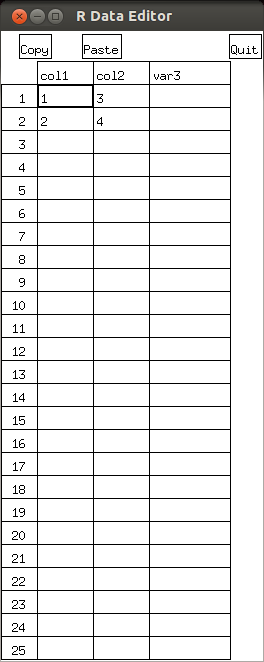

image(m，col=...)：行列 m をグラフィカルに表示
「col = ...」には以下の色指定関数を使用できる：
- grey()：グレースケールのカラーマップ
- heat.colors()：熱分布の可視化に適したカラーマップ
- topo.colors()：離散データの可視化に適したカラーマップ
- rainbow()：離散データの可視化に適した虹色のカラーマップ
- terrain()：地形データの可視化に適したカラーマップ
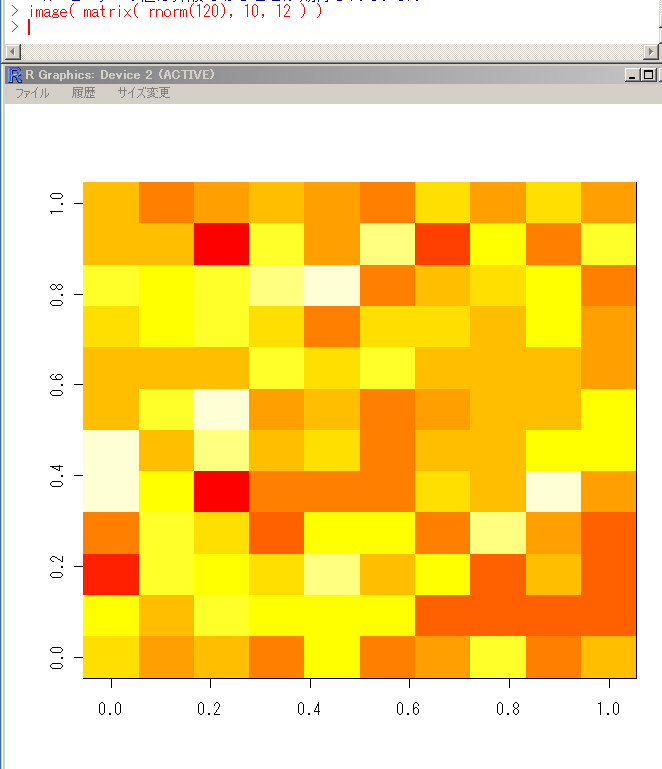
画像表示の例

リストに関する演算子と関数

length(L)：リスト L の長さを返す
L[]：リスト L の要素を取得する
- L[1]：1番目の要素を取得
- L[-1]：1番目の要素以外のすべての要素を取得
- L[1:3]：1から3番目までの要素を取得
- L[c(F,T,F,T)]：論理値による選択で2番目と4番目の要素を取得
- L[L>10]：値が10より大きい要素のみを取得
lapply(L，f)：リスト L の全要素に関数 f を適用し，新しいリストを生成する
```
L <- list(1, 2, 3)
lapply(L, function(x) (x * 2))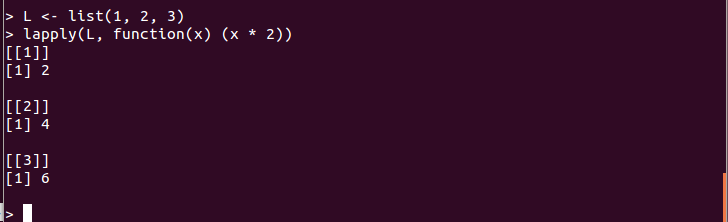
```

データフレームに関する演算子と関数

データフレームには，配列に使える演算子や関数の多くが適用可能である．データフレームに特有の関数は次の通りである．

$：列名（属性名）による要素の取り出し

出力はベクトル形式となる．

d <- data.frame( type = c(1:6),
name = c("apple", "orange", "strawberry", "watermelon", "melon", "banana"),
price = c(50, 20, 100, 150, 200, 100) )
d$type
d$name
d$price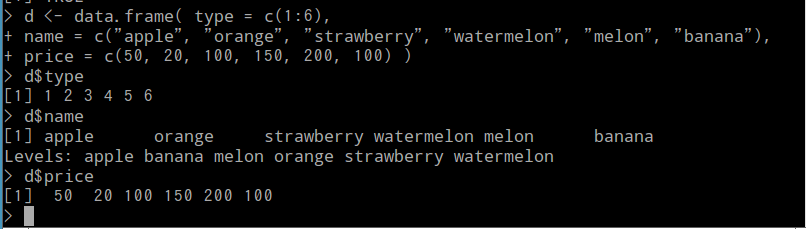

[＜列名のベクトル＞]：列名（属性名）の並びによる射影処理
出力はデータフレーム形式となる．
```
d[ "type" ]
d[ c("type", "name") ]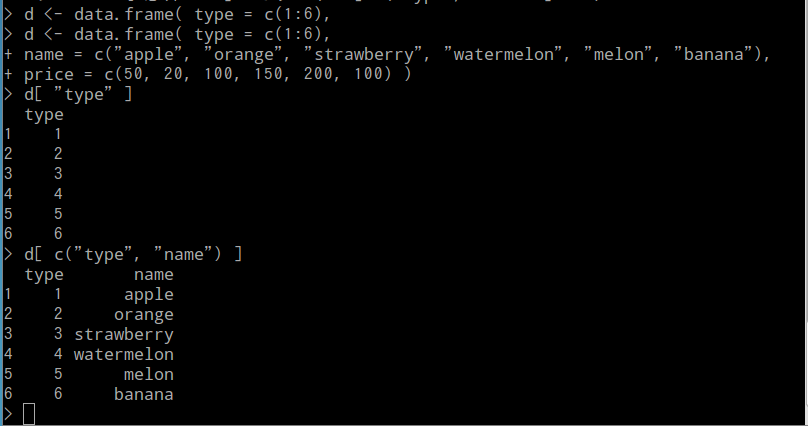
```
subset(d，属性名＜比較演算子＞＜値＞)：データフレーム d から指定した条件を満たす行を選択する
条件式による選択を実行する場合は，subset 関数の引数に条件式を記述する．
```
subset( d, name == "apple" )
subset( d, price > 140 )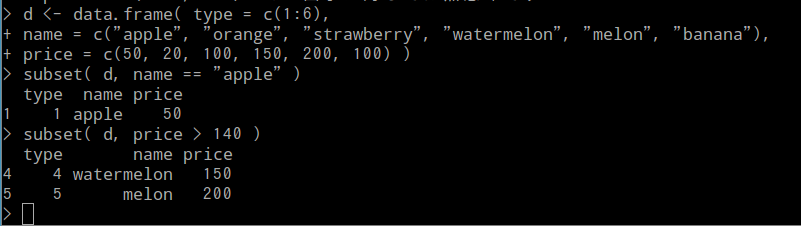
```
subset(d，属性名 %in% c(＜要素の並び＞))：データフレーム d から指定した値のリストに該当する行を選択する
データフレームから特定の値を持つ行を選択する場合は，subset() 関数と %in% 演算子を組み合わせて使用する．
```
subset( d, name %in% c( "apple", "orange", "banana") )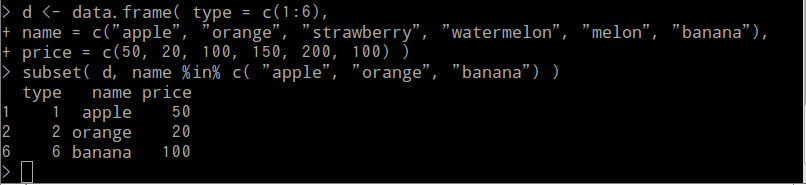
```

summary(d)：データフレーム d の基本統計量を要約して表示する

d <- data.frame( type = c(1:6),
name = c("apple", "orange", "strawberry", "watermelon", "melon", "banana"),
price = c(50, 20, 100, 150, 200, 100) )
summary(d)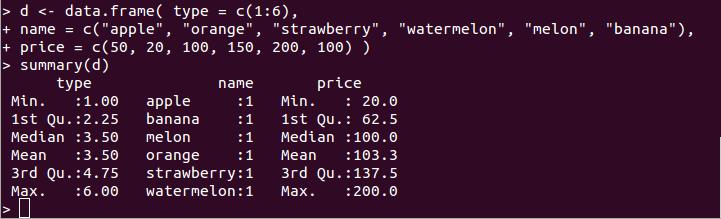

t(d)：データフレーム d の行列転置を実行する
行と列を入れ替える処理を行う関数であり，出力は行列形式となる．
data.frame( d，＜属性名＞ = ＜ベクトル＞ )：データフレーム d に新しい列を追加する
rbind( d，V )：データフレーム d に新しい行 V を追加する

merge(d1，d2，by.x=＜属性名＞，by.y=＜属性名＞)：2つのデータフレームを結合する

データフレームd2のno列とデータフレームd3のno列でのマージ例：

d2 <- data.frame( no = c(1, 2, 3), name=c("apple", "orange", "banana") )
d3 <- data.frame( no = c(1, 2, 3), color=c("red", "orange", "yellow") )
merge(d2, d3, by.x="no", by.y="no")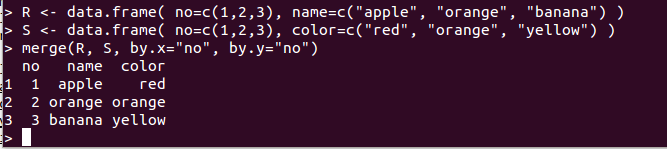

データフレームd2のname列とデータフレームd3のname列でのマージ例：

d2 <- data.frame(
name = c("apple", "orange", "rose", "rose"),
color = c("red", "orange", "red", "yellow"),
price = c(50, 20, 300, 450) )
d3 <- data.frame(
name = c("apple", "orange", "rose"),
type = c("fruits", "fruits", "flower") )
merge(d2, d3, by.x="name", by.y="name")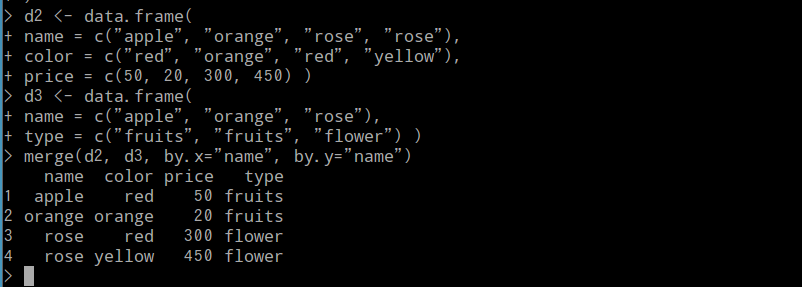

split(d，d$＜属性名＞)：指定した属性の値に基づいてデータフレーム d を分割する

d <- data.frame( type = c(1:6),
size = c("M", "S", "M", "M", "L", "S"),
price = c(120, 80, 110, 100, 200, 60) )
split(d, d$size)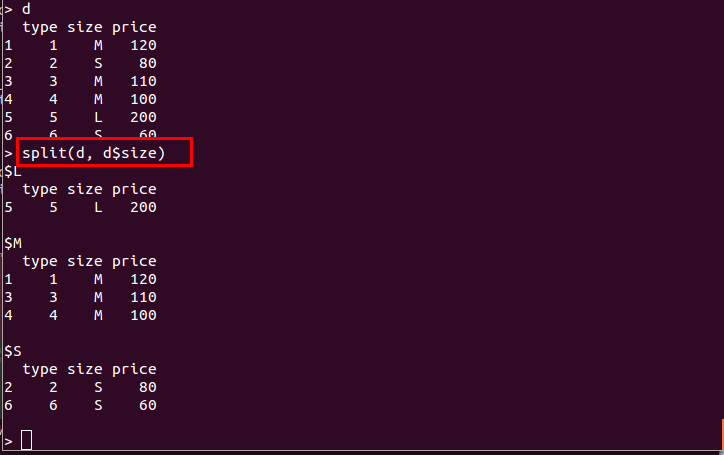

apply(d，＜次元の指定＞，f)：データフレーム d の行または列に関数 f を適用して新しいベクトルを生成する
次元の指定は以下の通り：
- 1：行方向の処理
- 2：列方向の処理
```
d <- data.frame( type = c(1:6),
name = c("apple", "orange", "strawberry", "watermelon", "melon", "banana"),
price = c(50, 20, 100, 150, 200, 100) )
apply(d, 2, range)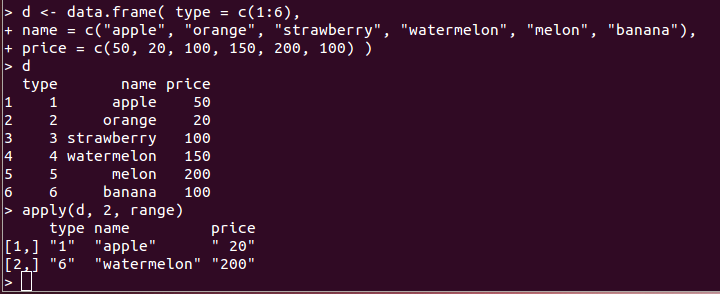
```
tapply(d$＜属性名＞，d$＜属性名＞，f)：データフレーム d を指定属性でグループ化し，各グループに関数 f を適用する
```
d <- data.frame( type = c(1:6),
size = c("M", "S", "M", "M", "L", "S"),
price = c(120, 80, 110, 100, 200, 60) )
tapply(d$price, d$size, mean)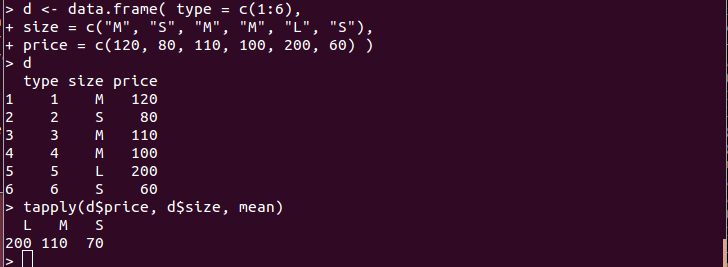
```
by(d$＜属性名＞，d$＜属性名＞，f)：tapplyと同様にグループ化と関数適用を行うが，より詳細な結果を表示する
```
d <- data.frame( type = c(1:6),
size = c("M", "S", "M", "M", "L", "S"),
price = c(120, 80, 110, 100, 200, 60) )
by(d$price, d$size, mean)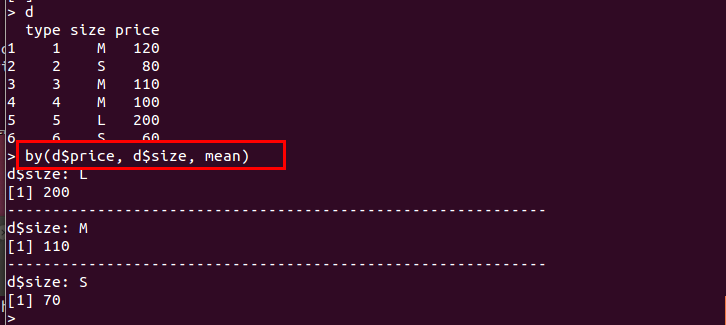
```
xtabs( ＜集計したい属性名＞ ~ ＜属性名＞，d )，xtabs( ＜集計したい属性名＞ ~ ＜属性名1＞ + ＜属性名2＞，d )：クロス集計表を生成する
```
data(warpbreaks)
table(warpbreaks$wool)
table(warpbreaks$tension)
table(warpbreaks$wool, warpbreaks$tension)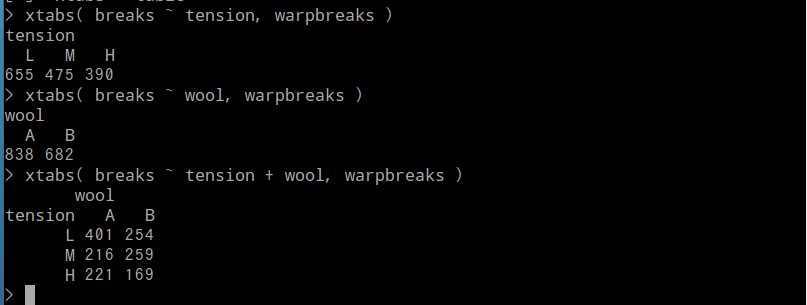
```

library(relimp); showData(d)：データフレーム d を別ウインドウで表示する

library(relimp)
d <- data.frame( type = c(1:6),
name = c("apple", "orange", "strawberry", "watermelon", "melon", "banana"),
price = c(50, 20, 100, 150, 200, 100) )
showData(d)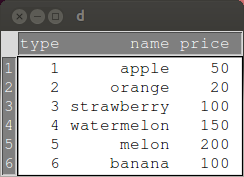

edit(d)：データフレーム d を対話的に編集する

d <- data.frame( type = c(1:6),
name = c("apple", "orange", "strawberry", "watermelon", "melon", "banana"),
price = c(50, 20, 100, 150, 200, 100) )
edit(d)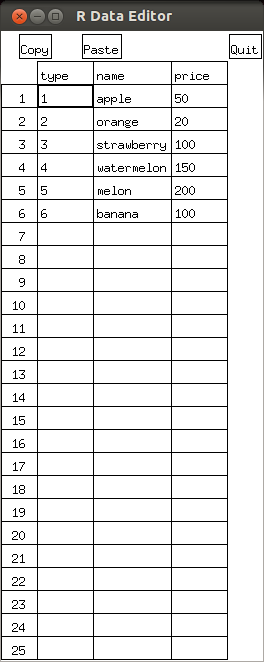

条件分岐と繰り返し

代表的な制御構造について説明する．

for(arg in range)は，指定された範囲の反復処理を行う．
while(cond) exprは，条件式が真である間，指定された処理を継続する．

for と while の例
if(条件式) {式} else {式}による条件分岐処理を行う．
- else句は省略可能であり，if(条件式) {式}の形式となる．
- 条件分岐は入れ子構造が可能であり，if(条件式) {式} else if (条件式) {式} ...の形式で記述できる．
if の例
ifelse(条件式，式1，式2)は，ベクトルの各要素に対して条件評価を実行する．
条件がベクトルの要素ごとに評価される．

グラフの概要

plot(X)：ベクトルXの散布図を描画する．
plot(X，Y)：ベクトルX，Yの散布図を作成する．
plot(m)：2次元の行列mに対する散布図を生成する．
```
plot( matrix( rnorm(100), 50, 2 ) )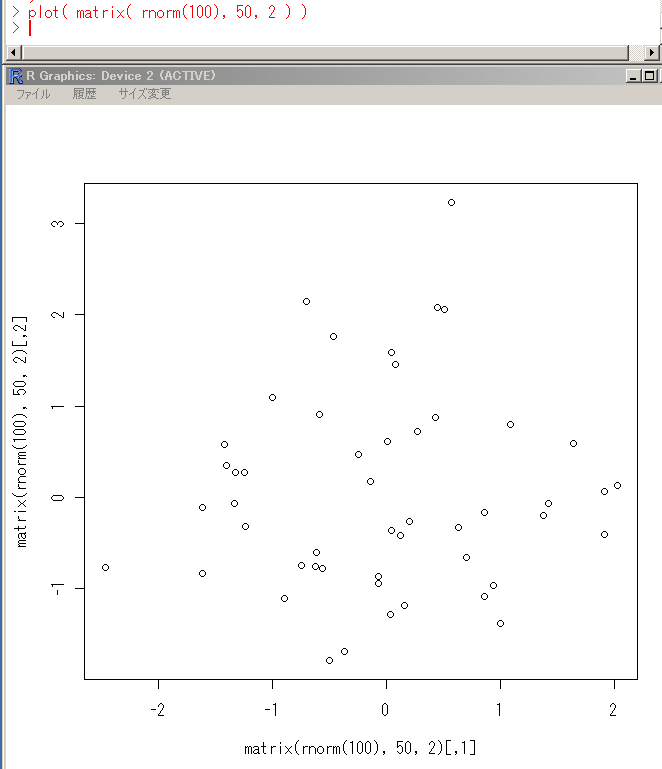
```
2次元の行列に対する散布図の例
plot(d)：データフレームdの散布図を生成する．
```
data(iris)
plot(iris, col=Species)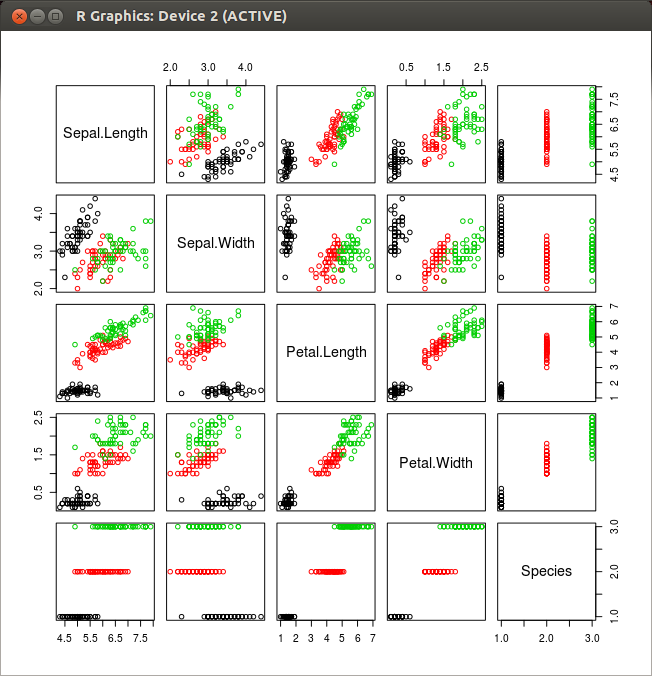
```
matplot()は，行列の各列x[,i]を独立した系列として，異なる記号を用いてプロットする．
```
matplot( cbind( c(1, 2, 3, 4), c(3, 4, 5, 6) ) )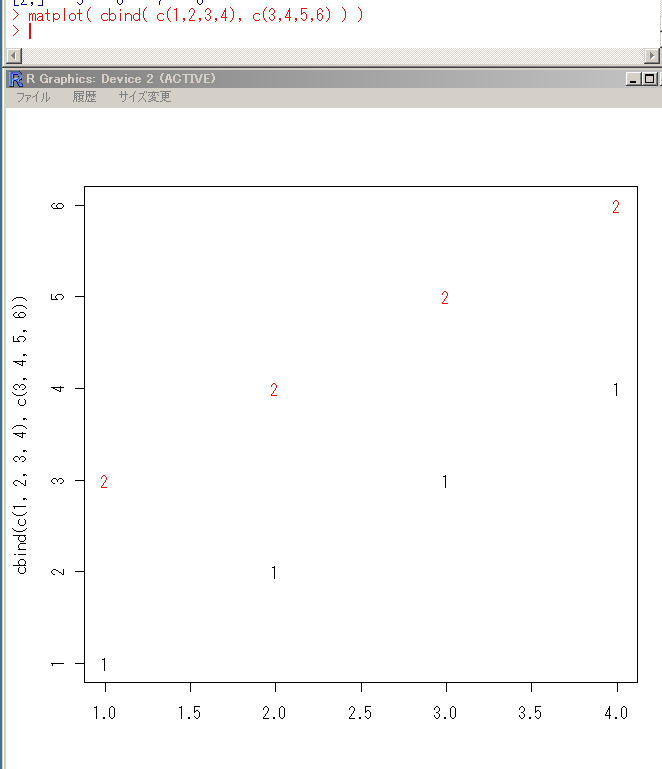
```
各列のプロットの例
hist(X)：ベクトルXのデータ分布をヒストグラムとして表示する．
```
data(iris)
hist( as.matrix( iris["Petal.Length"] ) )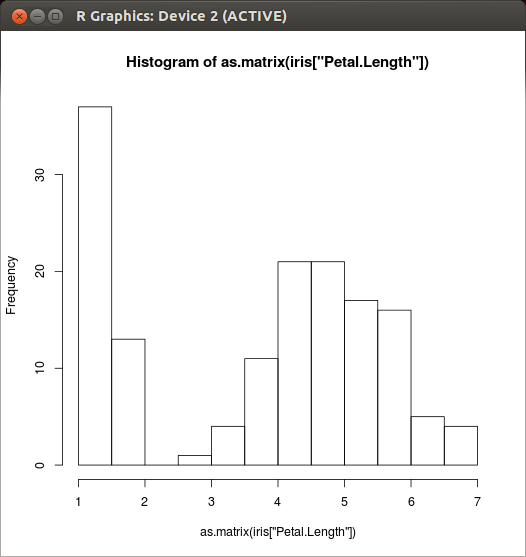
```
barplot(X)：ベクトルXのデータを棒グラフとして描画する．
legend()：グラフの凡例を追加する．
abline()：グラフに回帰直線を追加する．

統計解析関連の機能

回帰分析の手法と関数

線形回帰分析（lm関数）は，最も基本的な回帰分析手法である．

model <- lm(weight ~ height, data = dataset)
summary(model)

model2 <- lm(weight ~ height + age + gender, data = dataset)
summary(model2)

一般化線形モデル（glm関数）は，より複雑なモデルを扱うことができる関数である．

model3 <- glm(success ~ score + time,
             family = binomial(link = "logit"),
             data = dataset)
summary(model3)

model4 <- glm(count ~ factor1 + factor2,
             family = poisson(link = "log"),
             data = dataset)
summary(model4)

統計的検定手法

t検定（t.test関数）は，平均値の差の検定を行う．

t.test(x, mu = 0)

t.test(group1, group2, paired = FALSE)

t.test(pre, post, paired = TRUE)

カイ二乗検定（chisq.test関数）は，カテゴリカルデータの独立性を検定する．
```
chisq.test(table(factor1, factor2))

chisq.test(observed, p = expected_prob)
```

分散分析（aov関数）は，複数グループ間の平均値の差を検定する．

result <- aov(value ~ group, data = dataset)
summary(result)

result2 <- aov(value ~ factor1 * factor2, data = dataset)
summary(result2)

多変量解析手法

主成分分析（prcomp関数）は，データの次元を削減する手法である．

pca_result <- prcomp(data, scale. = TRUE)
summary(pca_result)

plot(pca_result$x[, 1:2])

因子分析（factanal関数）は，潜在変数を探索する手法である．

fa_result <- factanal(data, factors = 3, rotation = "varimax")
print(fa_result$loadings)

判別分析（lda関数）は，グループの分類を行う手法である．

library(MASS)
lda_result <- lda(group ~ ., data = training_data)
predictions <- predict(lda_result, newdata = test_data)

クラスター分析は，データをグループ化する手法である．

hc_result <- hclust(dist(data))
plot(hc_result)

km_result <- kmeans(data, centers = 3)
plot(data, col = km_result$cluster)

データ操作関連の機能

tidyverseパッケージ群

dplyrパッケージの主要関数は，データフレームを効率的に操作する．

library(dplyr)

result <- data %>%
    filter(age > 20) %>%
    select(name, age, score) %>%
    arrange(desc(score)) %>%
    group_by(age) %>%
    summarise(
        avg_score = mean(score),
        count = n()
    )

tidyrパッケージの主要関数は，データ形式の変換を行う．

library(tidyr)

long_data <- wide_data %>%
    pivot_longer(
        cols = c(score1, score2, score3),
        names_to = "test",
        values_to = "score"
    )

wide_data <- long_data %>%
    pivot_wider(
        names_from = test,
        values_from = score
    )

データ結合操作は，複数のデータフレームを組み合わせる．

inner_join(df1, df2, by = "id")

left_join(df1, df2, by = "id")

full_join(df1, df2, by = "id")

欠損値の処理方法

欠損値の確認は，データの品質を評価する重要なステップである．
```
sum(is.na(data))

colSums(is.na(data))

data[!complete.cases(data), ]
```
欠損値の除去は，完全なデータセットを得る最も単純な方法である．
```
clean_data <- na.omit(data)

data %>% drop_na(specific_column)
```

欠損値の補完は，データの情報量を保持する方法である．

library(tidyr)

data %>%
    mutate(score = replace_na(score, mean(score, na.rm = TRUE)))

data %>%
    fill(score, .direction = "down")

高度な補完手法は，より精密な欠損値の推定を行う．

library(mice)

imputed_data <- mice(data, m = 5, method = "pmm")
completed_data <- complete(imputed_data, 1)

プログラミング関連の機能

関数定義

基本的な関数定義は，次のように記述する．
```
square <- function(x) {
    return(x * x)
}
square(5)
```

デフォルト引数の設定が可能である．

greet <- function(name = "User") {
    paste("Hello,", name)
}
greet()
greet("Alice")

可変長引数の使用が可能である．

sum_all <- function(...) {
    args <- list(...)
    return(sum(unlist(args)))
}
sum_all(1, 2, 3)
sum_all(1, 2, 3, 4)

エラー処理

try()は，エラーが発生しても実行を継続する関数である．

result <- try(1 / 0, silent = TRUE)
if (class(result) == "try-error") {
    print("エラーが発生した")
}

tryCatch()は，エラー種別ごとに処理を定義する関数である．

result <- tryCatch(
    expr = {
        1 / 0
    },
    error = function(e) {
        print(paste("エラー:", e$message))
        return(NULL)
    },
    warning = function(w) {
        print(paste("警告:", w$message))
        return(NULL)
    }
)

stop()は，エラーを発生させる関数である．

divide <- function(x, y) {
    if (y == 0) {
        stop("0での除算はできない")
    }
    return(x / y)
}

warning()は，警告を発生させる関数である．

sqrt_safe <- function(x) {
    if (x < 0) {
        warning("負の値の平方根は虚数になる")
        return(NaN)
    }
    return(sqrt(x))
}

デバッグ方法

browser()は，コード内に一時停止点を設定する関数である．

complex_calc <- function(x) {
    y <- x * 2
    browser()
    z <- y ^ 2
    return(z)
}

debug()/undebug()は，関数のデバッグモードを設定/解除する関数である．
```
debug(complex_calc)
complex_calc(5)
undebug(complex_calc)
```

trace()は，関数の実行を追跡する関数である．

trace("complex_calc",
      tracer = quote(print(paste("y値:", y))),
      at = 2)

traceback()は，エラー発生時のコールスタックを表示する関数である．

f <- function(x) g(x)
g <- function(x) h(x)
h <- function(x) stop("エラー発生")
f(10)
traceback()

options(error = recover)は，エラー時にデバッガを起動する設定を行う関数である．
```
options(error = recover)
f(10)
```